Теоремы о пределах (правила предельного перехода)
Теорема 1.
,
где
.
Теорема 2.
.
Теорема 3.
Теорема 4.
.
Теорема 5.
.
Теорема 6.
.
В случае, когда функция определена в точке, то чтобы найти предел, можно вместо независимой переменной подставить её значение в предельной точке.
Пример 2. Найти
.
Решение:
В данном случае предел функции, стоящей
в знаменателе, при
отличен от нуля, поэтому можно применить
правила предельного перехода
.
Ответ.
.
Пример 3.
Найти
.
Решение.
Предел знаменателя
при
равен нулю. В данном случае воспользуемся
свойством бесконечно малой функции
(см. свойство 6). Функция
– бесконечно малая при
,
тогда обратная ей дробь
– бесконечно большая функция, а значит
.
Ответ.
.
Пример 4. Найти
.
Решение.
.
Ответ.
.
Очевидно, если
знаменатель дроби не обращается в ноль,
то чтобы найти такой предел, достаточно
в выражение функции подставить предельные
значения независимых переменных. Если
же знаменатель стремиться к нулю
,
а числитель к некоторому постоянному
числу, то при нахождении предела
используют свойство бесконечно малой
величины (см. свойство 6).
В случае
неопределенных выражений, характеризуемых
условно символами:
(будем называть их неопределенностями),
которые возникают при отыскании предела
выражений:
;
;
или
предел может существовать или не
существовать. В пределах такого типа,
требуются дополнительные преобразования
или специальные исследования. Рассмотрим
некоторые из них.
I.
Раскрытие неопределенности
в пределе отношения двух многочленов:
II.
Раскрытие
неопределенности
в пределе вида
.
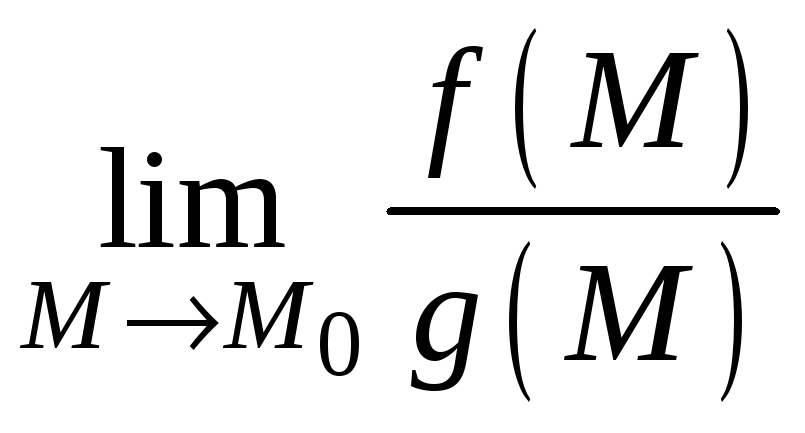а)
Если числитель и знаменатель –
многочлены, то чтобы раскрыть данную
неопределенность, необходимо числитель
и знаменатель разложить на множители
и сократить дробь. В некоторых случаях
удобнее разделить числитель и знаменатель
на критический множитель
(для функции одной переменной), или
воспользоваться определением предела.
b) Если дробь является иррациональным выражением, то в некоторых случаях, чтобы раскрыть данную неопределенность необходимо числитель и знаменатель дроби умножить на выражение, сопряженное иррациональному или применить подстановку.
III.
Раскрытие
неопределенности
в пределе вида
.
Чтобы раскрыть данную неопределенность, необходимо преобразовать разность в частное.
Пример 5.
Найти
.
Решение.
,
так как
и
,
.
Ответ.
.
Пример 6.
Найти
.
Решение.
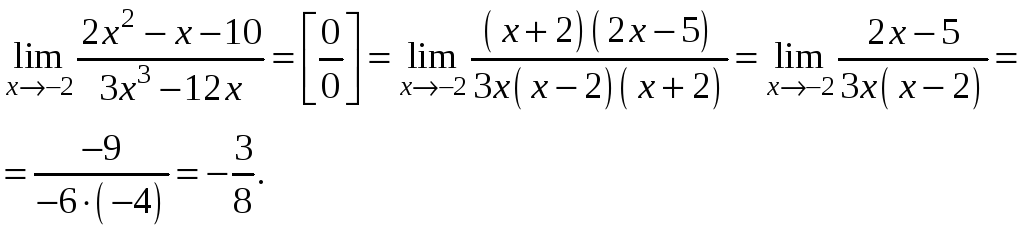
Ответ.
.
Пример 7.
Найти
.
Решение.
.
Разделим числитель и знаменатель на
критический множитель
,
тогда
.
Ответ.
.
Пример 8.
Найти
.
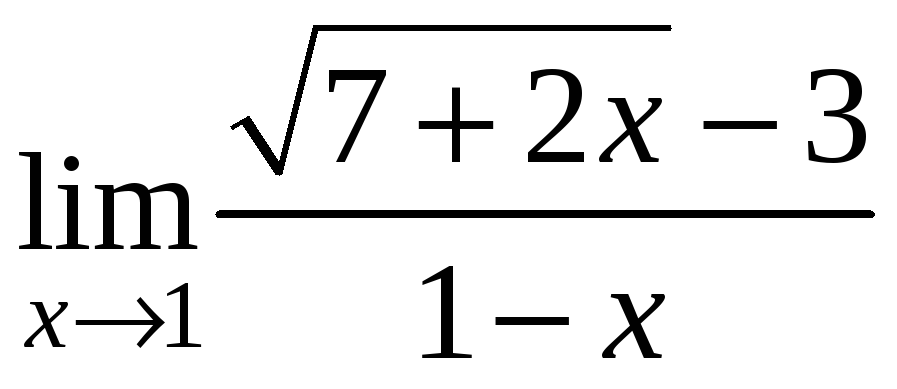Решение.
.
Умножим числитель
и знаменатель на выражение
– сопряженное числителю
:
..
Ответ.
.
Пример 9. Найти
.
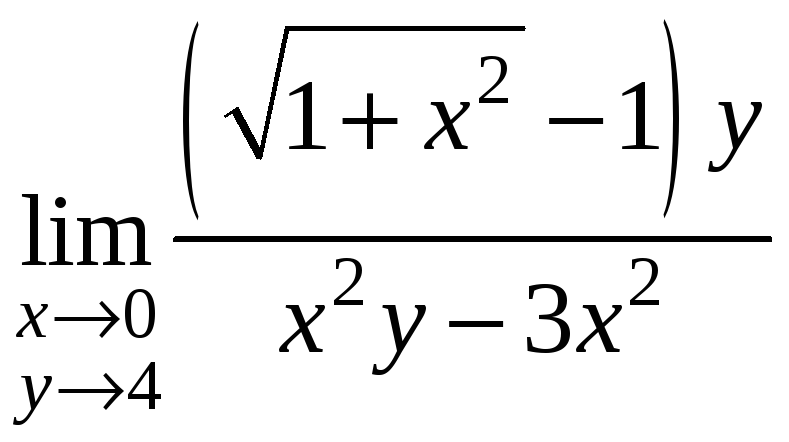
Решение. Умножим
числитель и знаменатель дроби на сумму
,
а в знаменателе вынесем за скобки
:
.
Ответ.
.
Пример 10.
Найти
.
Решение.
.
Выполним подстановку
при
.
.
Ответ.
.
Пример 11.
Найти
.
Решение.
.
Преобразуем разность в частное, выполнив
действие между дробями
Ответ.
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найти пределы.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23.
1.24.
1.25.
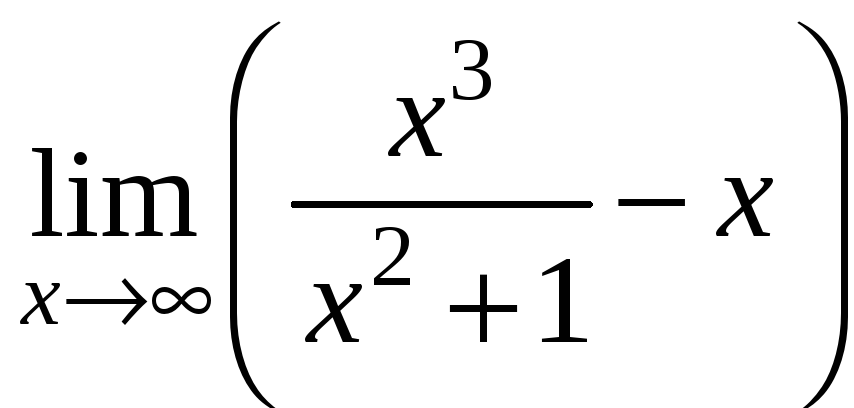
1.26.
1.27.
1.28.
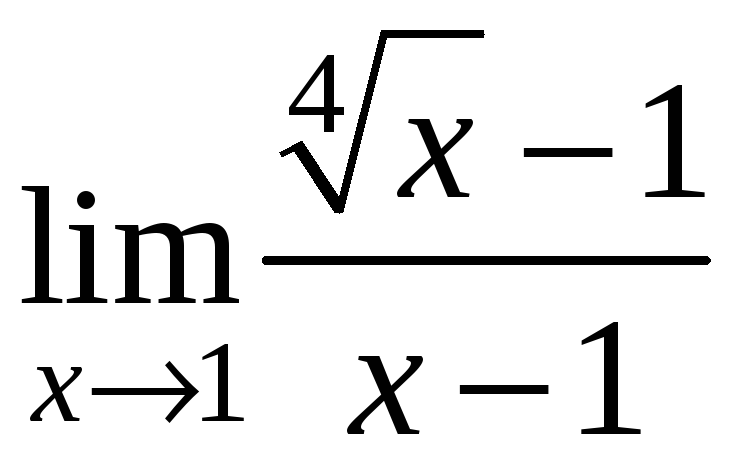
1.29.
1.30.
1.31.
1.32.
1.33.
1.34.
1.35.
1.36.
1.37.
1.38.
1.39.
1.40.
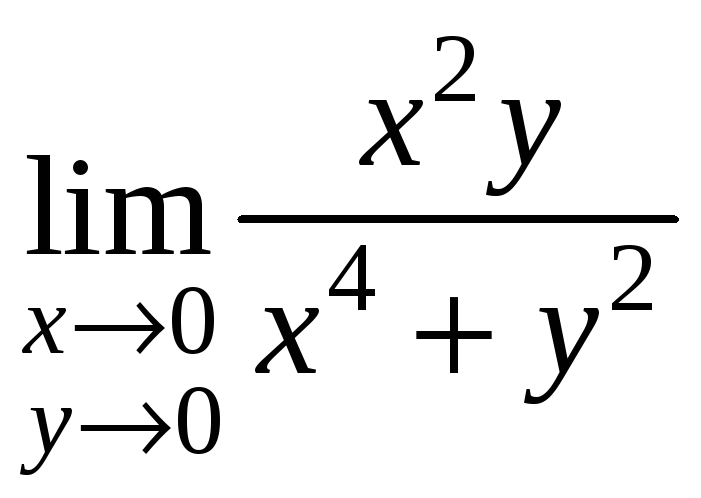
1.41.
1.42.
1.43.
1.44.
2. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ПО ТЕМЕ: