2.Неопределенность .
,
где
,
.
Затем, используя правило Лопиталя найти
и сравнить этот предел с единицей.
Тогда,
3.Неопределенности , , .
Пределы во всех трех случаях находят с помощью предварительного логарифмирования.
Пример 1.
Найти
.
Решение. Имеем
(здесь заменили
бесконечно малую на эквивалентную: 
).
Ответ.
.
Пример 2.
Найти
.
Решение. Применяя дважды правило Лопиталя, получим
.
Ответ.
Пример 3.
Найти
.
Решение. Имеем
.
Ответ.
.
Пример 4.
Найти
(неопределенность
).
Решение. Имеем
.
Ответ.
.
Пример 5.
Найти
(неопределенность
).
Решение. Имеем
.
Так как
,
то
.
Ответ.
.
Пример 6.
Найти
.
Решение. Пусть
,
прологарифмируем обе части равенства: 
.
Тогда
(здесь заменили
бесконечно малую величину на эквивалентную:
).
Таким образом
,
т.е.
.
Ответ.
.
Задачи для самостоятельного решения
7.1.
7.2.
7.3.
7.4.
7.5.
7.6.
7.7.
7.8.
7.9.
7.10.
7.11.
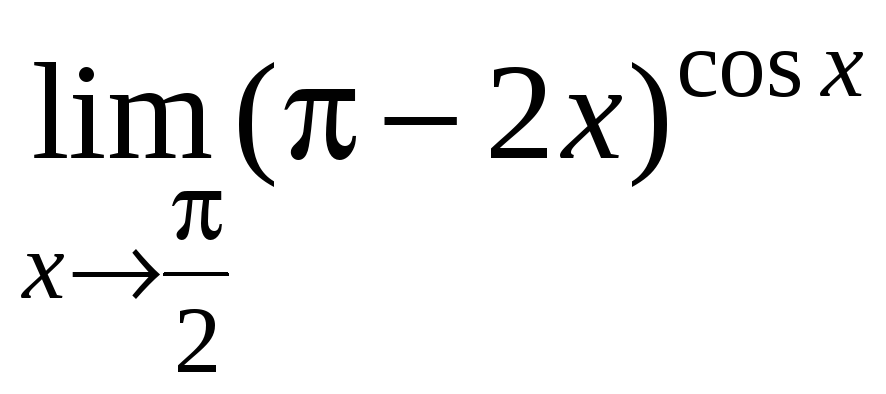
7.12.
7.13.
7.14.
7.15.
7.16.
8. Практическое занятие по теме: Общая схема исследования функции и построение графика
Для того чтобы построить график функции необходимо изучить ее свойства, используя пределы и производную.
Рассмотрим основные свойства функции.
Функция
,
заданная на симметричном относительно
начала координат промежутке, называется
четной
(нечетной),
если для любого значения
из этого промежутка выполняется
равенство
.
График четной
функции
симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Функция
называется периодической,
если существует число
такое, что для любого значения
из области определения функции
выполняется равенство
,
где
– наименьший
положительный период.
Если
– наименьший положительный период
функции, то число
,
где
– также является периодом функции.
Например, наименьшим
положительным периодом функций
и
является число
,
а для функций
и
это число
.
Из определения
периодической функции следует, что её
график будет «повторять» себя через
промежуток равный по длине наименьшему
положительному периоду
.
Поэтому достаточно построить график
такой функции на любом промежутке вида
и смещая построенный график вдоль оси
на отрезке длины
,
получим график функции
.
Функция
называется возрастающей
(убывающей) на некотором интервале,
если большим значениям аргумента
соответствуют большие (меньшие) значения
функции, т.е. если
,
то
.
Возрастающие и убывающие функции называются монотонными функциями. Интервал, на котором функция возрастает (убывает) называется интервалом возрастания (убывания) функции или интервалом монотонности.
Точка, в которой
производная
равна нулю или не существует, называется
критической
точкой.
Точка
из области определения функции
называется точкой
минимума (максимума)
этой функции, если существует такая
-
окрестность точки
,
что для всех
из этой
-
окрестности выполняется неравенство
.
Точки максимума и минимума функции
называются точками
экстремума функции,
а значения функции в этих точках
называются соответственно максимумом
и минимумом
функции,
или экстремумами
функции.
График функции
называется выпуклым
(вогнутым)
на некотором интервале, если касательная,
проведенная к графику функции в любой
точке с абсциссой из этого интервала,
расположена выше (ниже) графика функции
Точка графика функции, в которой график функции меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.
В абсциссе точки
перегиба производная второго порядка
равна нулю, или не существует.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремиться к нулю при неограниченном удалении от начала координат этой точки по кривой.
Асимптоты бывают вертикальными, наклонными и горизонтальными.
Вертикальная
асимптота:
,
где
‑ точка разрыва II–го
рода.
Наклонная
асимптота
:
,
где
. (8.1)
. (8.2)
Замечание.
Если хотя бы один из пределов (8.1) или
(8.2) не существует или равен бесконечности,
то график функции
наклонной асимптоты не имеет.
Горизонтальная
асимптота:
– прямая, параллельная оси
,
существует при
.
Тогда
.
(8.3)
Замечание.
Асимптоты графика функции
при
и при
могут
быть разными. Поэтому при нахождении
пределов (8.1), (8.2) и (8.3) следует отдельно
рассматривать случай, когда
и когда
.