
- •Дифференциальное исчисление
- •Содержание
- •Введение
- •Задачи для самостоятельного решения
- •Свойства бесконечно малых и бесконечно больших функций
- •Теоремы о пределах (правила предельного перехода)
- •Замечательные пределы. Сравнение бесконечно малых величин
- •Задачи для самостоятельного решения
- •Свойства эквивалентных бесконечно малых функций
- •Важнейшие эквивалентности
- •Задачи для самостоятельного решения
- •3. Практическое занятие по теме: Непрерывность функции. Точки разрыва и их классификация
- •Задачи для самостоятельного решения
- •4. Практическое занятие по теме: вычисление производной функции одной переменной. Таблица производных. Нахождение частных производных. Производная сложной функции
- •Правила дифференцирования результатов арифметических действий над функциями
- •Геометрический смысл производной функции одной переменной
- •Геометрический смысл частных производных функции двух переменных
- •Задачи для самостоятельного решения
- •5. Практическое занятие по теме: производная неявной функции однОй и нескольких переменных. Производная функции, заданной параметрически. Логарифмическое дифференцирование
- •Производная неявно заданной функции.
- •Производная функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Задачи для самостоятельного решения
- •6. Практическое занятие по теме: Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков
- •Основные свойства дифференциала
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •7. Практическое занятие по теме: Правило Лопиталя
- •1.Неопределенность
- •2.Неопределенность .
- •3.Неопределенности , , .
- •Задачи для самостоятельного решения
- •8. Практическое занятие по теме: Общая схема исследования функции и построение графика
- •Алгоритм исследования функции
- •Задачи для самостоятельного решения
- •Библиографический список
Задачи для самостоятельного решения
Найти указанные производные.
6.23.
![]() ,
,
![]()
6.24.
 ,
,

6.25.
![]() ,
,
![]()
6.26.
![]() ,
,

6.27.
![]() ,
,
![]()
6.28.
![]() .
Показать, что
.
Показать, что
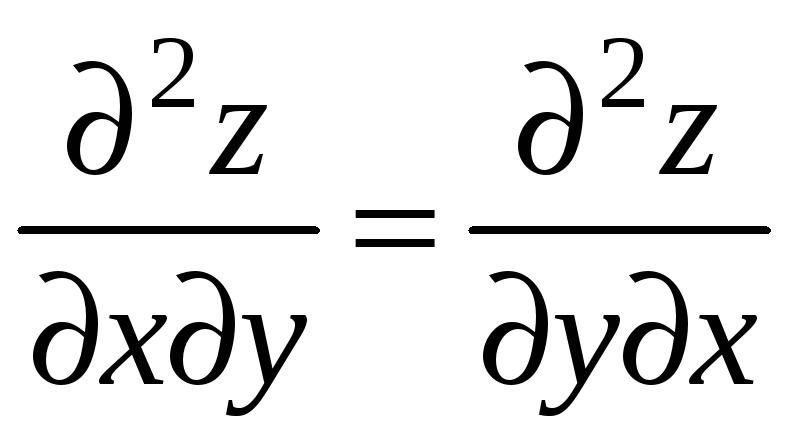 .
.
6.29.
![]() ,
, ![]()
6.30.
![]() .
Найти
.
Найти
![]() ,
,
![]() .
.
6.31.
![]() ,
,
![]()
6.32.
![]() .
Найти
.
Найти
![]() ,
,
![]() .
.
6.33.
![]() ,
,
![]()
6.34.
![]() ,
,

6.35.
![]() ,
,
![]()
6.36.![]() ,
,

6.37.
![]() ,
,

6.38. Доказать, что
функция
![]() удовлетворяет соотношению
удовлетворяет соотношению
![]() .
.
6.39.![]() .
Убедиться, что
.
Убедиться, что и
и
 .
.
6.40.
![]() .
Проверить, что
.
Проверить, что
 .
.
6.41.
![]() .
Показать, что
.
Показать, что
 .
.
6.42.

6.43.
![]() ,
,

6.44.
![]() ,
,

6.45.
![]() ,
,

6.46.
![]() ,
,

6.47.
![]()
6.48.

6.49.
![]()
6.50.
![]() ,
,

6.51. Найти все
частные производные второго порядка
для функции
![]() .
.
Определение.
Дифференциалом
![]() ‑го
порядка функции
‑го
порядка функции
![]() называется дифференциал от дифференциала
называется дифференциал от дифференциала
![]() ‑го
порядка
‑го
порядка
![]() .
.
Если
![]() ‑ независимая переменная, то
дифференциалы
высших порядков
вычисляются по формулам:
‑ независимая переменная, то
дифференциалы
высших порядков
вычисляются по формулам:
![]() .
.
Определение.
Полным
дифференциалом
![]() ‑го
порядка функции
‑го
порядка функции
![]() называется полный дифференциал от
полного дифференциала
называется полный дифференциал от
полного дифференциала
![]() ‑го
порядка
‑го
порядка
![]() .
.
Если
![]() ,
,
![]() – независимые переменные, то полные
дифференциалы
функции
– независимые переменные, то полные
дифференциалы
функции
![]() вычисляются по формулам:
вычисляются по формулам:
 ,
,
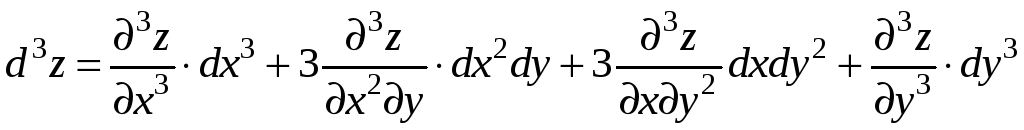
и т.д.
Пример 15.
![]() .
Найти
.
Найти
![]() .
.
Решение. Имеем
 ,
,
 .
.
Ответ.
![]() .
.
Пример 16.
![]() .
Найти
.
Найти
![]() .
.
Решение. Имеем
 .
Тогда
.
Тогда

 ,
,
 .
.
Следовательно,
 .
.
Ответ.
 .
.
Задачи для самостоятельного решения
6.52.
![]() ,
,
![]()
6.53.
![]() ,
,
![]()
6.54.
![]() ,
,
![]()
6.55.
![]() ,
,![]()
6.56.
![]() ,
,
![]()
6.57.
![]() ,
,
![]()
6.58.
![]() ,
,
![]()
7. Практическое занятие по теме: Правило Лопиталя
Теорема.
Пусть функции
![]() и
и
![]() непрерывны и дифференцируемы в
окрестности точки
непрерывны и дифференцируемы в
окрестности точки
![]() и обращаются в ноль в этой точке:
и обращаются в ноль в этой точке:
![]() ,
при этом
,
при этом
![]() в окрестности точки
в окрестности точки
![]() .
Если отношение производных этих функций
имеет предел при
.
Если отношение производных этих функций
имеет предел при
![]() ,
равный
,
равный
![]() ,
то отношение самих функций также имеет
предел при
,
то отношение самих функций также имеет
предел при
![]() ,
равный пределу отношения их производных,
т.е.
,
равный пределу отношения их производных,
т.е.

![]() (7.1)
(7.1)
Формула (7.1)
справедлива и при
![]() ,
и в том случае, когда обе функции
,
и в том случае, когда обе функции
![]() и
и
![]() стремятся к бесконечности.
стремятся к бесконечности.
Таким образом, теорема сводит предел отношения бесконечно малых (бесконечно больших) функций к пределу отношения производных этих функций, если последний существует.
Отыскание предела отношения двух функций с использованием выше приведенной теоремы называется правилом Лопиталя.
Правило Лопиталя
применяется для раскрытия неопределенностей
вида
![]() и
и
![]() ,
которые называются основными.
,
которые называются основными.
Иногда, после
перехода от
 к
к
 по правилу Лопиталя сохраняется
неопределенность отношения производных.
Тогда правило Лопиталя применяют
повторно, а в некоторых случаях и не
один раз.
по правилу Лопиталя сохраняется
неопределенность отношения производных.
Тогда правило Лопиталя применяют
повторно, а в некоторых случаях и не
один раз.
На каждом этапе применения правила Лопиталя следует пользоваться упрощающими отношение тождественными преобразованиями.
Неопределенности
вида
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() сводятся к двум основным видам
сводятся к двум основным видам
![]() и
и
![]() ,
путем тождественных преобразований.
,
путем тождественных преобразований.
1.Неопределенность
![]() ,
где
,
где
![]() ,
,

 .
.
