
- •Дифференциальное исчисление
- •Содержание
- •Введение
- •Задачи для самостоятельного решения
- •Свойства бесконечно малых и бесконечно больших функций
- •Теоремы о пределах (правила предельного перехода)
- •Замечательные пределы. Сравнение бесконечно малых величин
- •Задачи для самостоятельного решения
- •Свойства эквивалентных бесконечно малых функций
- •Важнейшие эквивалентности
- •Задачи для самостоятельного решения
- •3. Практическое занятие по теме: Непрерывность функции. Точки разрыва и их классификация
- •Задачи для самостоятельного решения
- •4. Практическое занятие по теме: вычисление производной функции одной переменной. Таблица производных. Нахождение частных производных. Производная сложной функции
- •Правила дифференцирования результатов арифметических действий над функциями
- •Геометрический смысл производной функции одной переменной
- •Геометрический смысл частных производных функции двух переменных
- •Задачи для самостоятельного решения
- •5. Практическое занятие по теме: производная неявной функции однОй и нескольких переменных. Производная функции, заданной параметрически. Логарифмическое дифференцирование
- •Производная неявно заданной функции.
- •Производная функции, заданной параметрически.
- •Логарифмическое дифференцирование.
- •Задачи для самостоятельного решения
- •6. Практическое занятие по теме: Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков
- •Основные свойства дифференциала
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •7. Практическое занятие по теме: Правило Лопиталя
- •1.Неопределенность
- •2.Неопределенность .
- •3.Неопределенности , , .
- •Задачи для самостоятельного решения
- •8. Практическое занятие по теме: Общая схема исследования функции и построение графика
- •Алгоритм исследования функции
- •Задачи для самостоятельного решения
- •Библиографический список
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВНИЯ
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ФУНДАМЕНТАЛЬОЙ ПОДГОТОВКИ
Ю.А. ТЕРЕЩЕНКО, В. А. ИГНАТОВА
Дифференциальное исчисление
Учебное пособие
к практическим занятиям
Красноярск 2008
Содержание
ВВЕДЕНИЕ 4
ФУНКЦИЯ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, ОБЛАСТЬ ОПРЕДЕЛЕНИЯ, СПОСОБЫ ЗАДАНИЯ. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ И ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ. СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ 5
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИН 16
Непрерывность функции. Точки разрыва и их классификация 27
ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ. ТАБЛИЦА ПРОИЗВОДНЫХ. НАХОЖДЕНИЕ ЧАСТНЫХ ПРОИЗВОДНЫХ. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ 31
ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ ОДНОй И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ 43
Дифференциал функции одной и нескольких переменных, применение дифференциалов в приближенных вычислениях. Производные и дифференциалы высших порядков 50
Правило Лопиталя 61
Общая схема исследования функции и построение графика 65
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 74
Введение
Математический анализ – большая область математики, связанная с понятием функции, производной и интеграла. Аппарат математического анализа используется в других областях математики, таких как дифференциальные уравнения, функции комплексного переменного, дифференциальная геометрия, вариационное исчисление и т.д. Таким образом, математический анализ – один из курсов, составляющий фундамент математического образования инженера любого профиля.
Один из основных разделов математического анализа – дифференциальное исчисление, центральным понятием которого является понятие производной. Производная широко применяется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различных процессов. Основные теоремы дифференциального исчисления позволяют построить мощный аппарат для исследования поведения функции.
В данном учебном пособии сначала рассматриваются практические занятия по темам, с которых традиционно начинают знакомство с математическим анализом, а именно: понятие функции, способы ее задания и свойства, предел функции, раскрытие неопределенностей, непрерывность функции, точки разрыва. Далее в пособии представлены практические занятия по разделу «Дифференциальное исчисление», в которых раскрываются понятия и геометрический смысл производной функции одной переменной и частных производных функции двух переменных, проиллюстрированы правила дифференцирования основных элементарных функций, способы нахождения производных функций, заданных различными способами; подробно описаны методы исследования поведения функции одной переменной, в частности алгоритмы нахождения точек экстремума, точек перегиба, асимптот.
В начале каждой темы кратко излагаются основные теоретические сведения (определения, теоремы, формулы), необходимые для решения последующих задач. Затем приводится достаточно большое количество примеров с подробными решениями, даются задачи и упражнения для самостоятельной работы. При подборе задач и примеров были использованы различные сборники задач по высшей математике, представленные в библиографическом списке.
Более подробно с теоретическим материалом по всем темам практических занятий можно познакомиться в конспекте лекций по разделу «Дифференциальное исчисление» тех же авторов, поскольку конспект лекций и учебное пособие для практических занятий по этому разделу образуют единый учебно – методический комплекс.
Данное учебное пособие может быть использовано как под руководством преподавателя на занятии, так и для самостоятельного изучения материала.
1. Практическое занятие по теме:
ФУНКЦИЯ ОДНОЙ И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, ОБЛАСТЬ ОПРЕДЕЛЕНИЯ, СПОСОБЫ ЗАДАНИЯ. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ И ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ. СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
Пусть даны
![]() и
и
![]() – переменные величины,
– переменные величины,
![]() и
и
![]() – области изменения этих величин.
– области изменения этих величин.
Определение.
Если каждому значению величины
![]() по некоторому закону соответствует
единственное значение величины
по некоторому закону соответствует
единственное значение величины
![]() ,
то говорят, что задана
функция
,
то говорят, что задана
функция
![]() ,
или что величины
,
или что величины
![]() и
и
![]() связаны между собой функциональной
зависимостью. При этом,
связаны между собой функциональной
зависимостью. При этом,
![]() – аргумент
функции
(независимая
переменная),
– аргумент
функции
(независимая
переменная),
![]() – значение
функции
(зависимая
переменная),
– значение
функции
(зависимая
переменная),
![]() – закон
соответствия,
– закон
соответствия,
![]() – функция одной независимой переменной.
– функция одной независимой переменной.
Множество
![]() называется
областью
определения функции
называется
областью
определения функции
![]() и обозначается
и обозначается
![]() .
Множество
.
Множество
![]() называется областью
значений функции
называется областью
значений функции
![]() и обозначается
и обозначается
![]() .
.
Для функции одной
переменной
![]() областью определения
областью определения
![]() является интервал координатной оси
является интервал координатной оси
![]() или вся координатная ось.
или вся координатная ось.
Определение.
Если областью существования функции
![]() служит множество натуральных чисел
служит множество натуральных чисел
![]() ,
то функцию
,
то функцию
![]() называют последовательностью
и обозначают
называют последовательностью
и обозначают
![]() ,
,
![]() ,
,
![]() и т. д.
и т. д.
Пусть даны
![]() и
и
![]() – переменные величины,
– переменные величины,
![]() – область изменения пар чисел
– область изменения пар чисел
![]() ,
а
,
а
![]() – область изменения
– область изменения
![]() .
.
Определение.
Если каждой
паре чисел
![]() по некоторому закону соответствует
единственное значение величины
по некоторому закону соответствует
единственное значение величины
![]() ,
то говорят, что задана функция
,
то говорят, что задана функция
![]() .
При этом
.
При этом
![]() – аргументы функции (независимые
переменные),
– аргументы функции (независимые
переменные),
![]() – значение функции (зависимая переменная),
– значение функции (зависимая переменная),
![]() – закон соответствия,
– закон соответствия,
![]() – функция
двух независимых переменных,
– функция
двух независимых переменных,
![]() – область определения функции,
– область определения функции,
![]() – область значений функции.
– область значений функции.
Для функции двух
переменных
![]() область определения
область определения
![]() является часть координатной плоскости
является часть координатной плоскости
![]() или вся координатная плоскость.
или вся координатная плоскость.
Определение.
Если каждой совокупности переменных
величин
![]() по некоторому закону соответствует
единственное значение
по некоторому закону соответствует
единственное значение
![]() ,
то говорят, что задана функция
,
то говорят, что задана функция
![]() – функция
– функция
![]() независимых переменных.
независимых переменных.
Для функции трех
переменных
![]() область определения функции геометрически
представляется в виде части трехмерного
пространства.
область определения функции геометрически
представляется в виде части трехмерного
пространства.
Для функции
![]() переменных, при
переменных, при
![]() ,
область определения невозможно
представить геометрически.
,
область определения невозможно
представить геометрически.
Наиболее распространены следующие способы задания функции: аналитический, графический и табличный. Подробно рассмотрим аналитический способ задания, который состоит в том, что дается формула, с помощью которой по значениям независимой переменной (независимых переменных) можно получить соответствующие им значения функции.
Функция, заданная аналитическим способом может быть задана: явно, неявно и параметрически.
Функция называется
явно
заданной,
если она задана уравнением
![]()
![]() ,
разрешенным относительно зависимой
переменной
,
разрешенным относительно зависимой
переменной
![]() (зависимой переменной
(зависимой переменной
![]() ).
).
Функция называется
неявно
заданной,
если она задана уравнением
![]() – для функции одной переменной (
– для функции одной переменной (![]() – для функции двух переменных), не
разрешенным относительно зависимой
переменной
– для функции двух переменных), не
разрешенным относительно зависимой
переменной
![]() (зависимой переменной
(зависимой переменной
![]() ).
).
Аналогично
определяется неявно заданная функция
![]() независимых переменных вида
независимых переменных вида
![]() ,
где
,
где
![]() .
.
Функция называется
параметрически
заданной,
если сама функция и её аргумент (аргументы)
заданы аналитическими выражениями,
зависящими от одного и того же параметра
![]() :
:
 – функция одной
переменной;
– функция одной
переменной;
 – функция двух переменных.
– функция двух переменных.
Пример 1. Найти и изобразить графически область определения функций.
а)
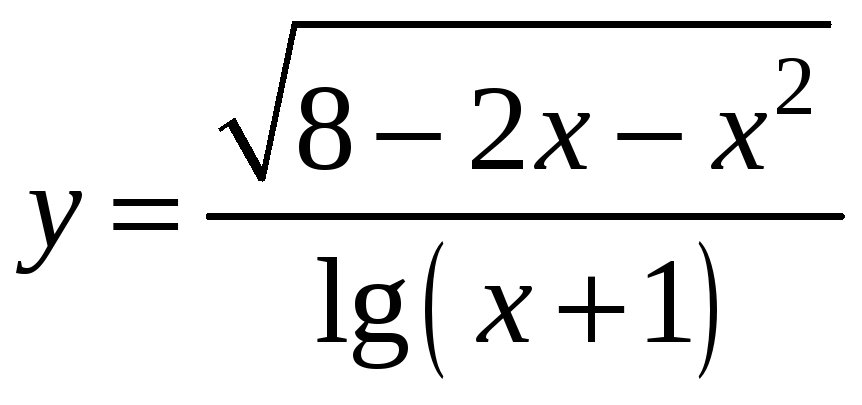 .
.
Решение. Функция имеет смысл, если

Найдем решение каждого неравенства в отдельности:
1)
![]() .
Решим неравенство методом интервалов.
.
Решим неравенство методом интервалов.
![]() :
:
т .е.
.е.
![]() .
.
2)
![]() ,
,
![]() .
.
3)
![]() ,
,
![]() .
.
Нанесем все
полученные интервалы на ось
![]() .
Их пересечение – и есть решение системы
неравенств.
.
Их пересечение – и есть решение системы
неравенств.
Т аким
образом
аким
образом
![]()
Ответ.
![]()
б)
![]() .
.
Решение.
![]() .
Значит, областью определения является
часть плоскости
.
Значит, областью определения является
часть плоскости
![]() ,
координаты точек которой, удовлетворяют
неравенству
,
координаты точек которой, удовлетворяют
неравенству
![]() ,
т.е. часть плоскости
,
т.е. часть плоскости
![]() ,
расположенная внутри параболы
,
расположенная внутри параболы
![]() .
Так как точки параболы не удовлетворяют
неравенству, то она изображается
пунктирной линией (см. рис.1.1).
.
Так как точки параболы не удовлетворяют
неравенству, то она изображается
пунктирной линией (см. рис.1.1).

