Свойство полноты множества вещественных чисел.

Теорема (свойство полноты множества вещественных чисел). Пусть А и В непустые подмножества множества вещественных чисел, обладающие следующим свойством:

хА и уВ ху, тогда существует такое действительное число с, что хсу.

хА и уВ: ху сR: хсу.

Замечание. Множество рациональных чисел не обладает свойством полноты.

Пример. Покажем, опираясь на эту теорему, что на множестве действительных чисел уравнение х²=2 имеет решение.

Рассмотрим множества А={x>0: x²<2} и B={y>0: y²>2}

Допустим, что х>yт.к. x,y>0, то x²>y²x²>2 – получили противоречие.

Следовательно, по свойству полноты, сR: xA и yB xcy.

Покажем, что сА, т.е. условие с²<2 не выполняется.

Допустим, что с²<2. Тогда взяв достаточно большое n <2, т.е.

с²+2с+<22с+<2-с²

Тогда с+А, что противоречит тому, что xcy.

Аналогично, через (с-) показывается, что сВ, т.е. не выполняется с²>2.

Следовательно, с²=2.

Плотность множества рациональных чисел в r.

Теорема. Между любыми вещественными числами находится бесконечное множество рациональных чисел. (Т.е. множество Q всюду плотно в R).

Доказательство. Возьмем числа a b (b>0) a<b, a,bR. Представим число b в виде бесконечной десятичной дроби:b=b₀,b₁b₂…

Построим приближения: ₁=b₀,b₁, ₂=b₀,b₁b₂,…,_k=b₀,b₁b₂…b_k и т.д.

Получим бесконечное множество рациональных чисел.

Тогда, т.к. b>0, то все _k<b.

Если из b вычесть _k, то b-_k=0,b_k+1b_k+2 – эта разность будет сколь угодно мала.

Следовательно, k₀: kk₀ b-_k<b-a_k>a, т.е. a<_k<b kk₀

Т.е. между числами а и b – множество рациональных чисел.

Если b0, то рассматриваются –b и –а. ч.т.д.

Промежутки числовой прямой.

Рассмотрим подмножества R.

a и b могут быть равны .

Модуль числа.

Определение. Модулем числа а называется расстояние от начала вещественной оси (0) до точки, изображающей а.

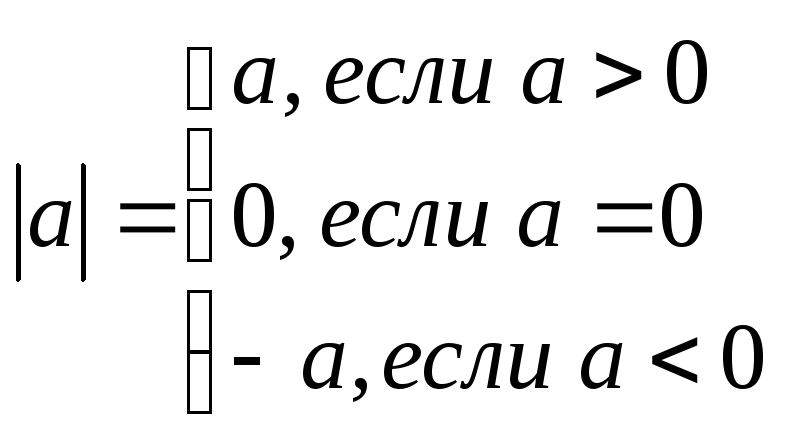
Свойства модуля.

1)

2)

3)

4) aa

5) -a=a

6) a+ba+b (a₁+a₂+…+a_na₁+a₂+…+a_n)

Ограниченные числовые множества. Границы числовых множеств.

Пусть А некоторое множество вещественных чисел.

Определение. Множество А называется ограниченным сверху, если

:. Число с – верхняя граница множества А. (рисунок)

Определение. Множество А называется ограниченным снизу, если

:. Число с – нижняя граница множества А. (рисунок)

Определение. Множество А называется ограниченным, если оно ограниченно и сверху, и снизу, т.е. если

:. Число с – верхняя граница множества А. (рисунок)

Множество верхних и нижних границ бесконечно.

Пусть А – числовое множество. Пусть : , тогда  - максимальный элемент множества А: =max A.

Пусть : , тогда  - минимальный элемент множества А: =min A.

Пример. А={1,} 1=max A.

A={x: 0<x<1} – нет максимума и минимума.

Пусть А – ограниченное сверху множество.

Определение. Наименьшая из всех верхних границ множества А называется точной верхней границей множества А (супремум – sup A).

Пусть А – ограниченное снизу множество.

Определение. Наибольшая из всех нижних границ множества А называется точной нижней границей множества А (инфимум – inf A).

Утверждение. Каждое ограниченное сверху множество имеет точную верхнюю границу.

Каждое ограниченное снизу множество имеет точную нижнюю границу.

Доказательство. Пусть А – ограниченное сверху множество.

В – множество всех верхних границ множества А, тогда

и

Поэтому, по свойству полноты множества R

: и , т.е.  - sup A. Ч.т.д.