Министерство аграрной политики и продовольствия Украины

Государственное агентство рыбного хозяйства Украины

Керченский государственный морской технологический университет

Факультет технологический

Кафедра «Экология моря»

Реферат

По дисциплине: Высшая математика

На тему: «Элементарные функции»

Выполнил

Студ. группы ЭМ-1

Надуда А. О.

Проверила

доц. Подольская О. Г.

Керчь, 2011

Степенная функция

Степенна́я фу́нкция — функция y = xa, где a (показатель степени) — некоторое вещественное число. К степенным часто относят и функцию вида y = kxa, где k — некоторый масштабный множитель. Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом.

Область определения

Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при x > 0. Если a > 0, то функция определена также и при x = 0, иначе нуль является её особой точкой.

Рациональный показатель степени

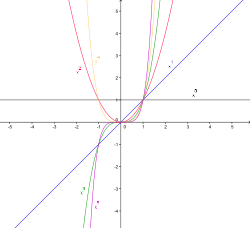
• Графики степенной функции при натуральном показателе n называются параболами порядка n. При a = 1 получается функция y = kx, называемая прямой пропорциональной зависимостью.

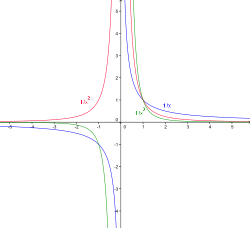
• Графики функций вида y = x ^{− n}, где n — натуральное число, называются гиперболами порядка n. При a = − 1 получается функция 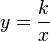, называемая обратной пропорциональной зависимостью.

• Если 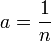, то функция есть арифметический корень степени n.

Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: T = kA^{3 / 2} (полукубическая парабола).

• 

Параболы порядка n:     n = 0      n = 1      n = 2      n = 3      n = 4      n = 5

• 

Гиперболы порядка n:     n = − 1      n = − 2      n = − 3

Свойства

• Функция непрерывна и неограниченно дифференцируема во всех точках, в окрестности которых она определена. Нуль, вообще говоря, является особой точкой; например, функция 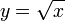определена в нуле и его правой окрестности, но её производная 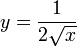в нуле не определена.

• В интервале 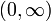функция монотонно возрастает при a > 0 и монотонно убывает при a < 0. Значения функции в этом интервале положительны.

• Производная функции:

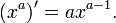
• Неопределённый интеграл:

  • Если , то

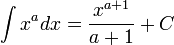
  • При a = − 1 получаем:

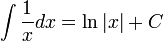
Комплексная функция

Степенная функция комплексного переменного z определяется формулой:

Здесь показатель степени c — некоторое комплексное число.

Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также многозначна. При натуральном показателе степени функция y = zⁿ однозначна и n-листна.

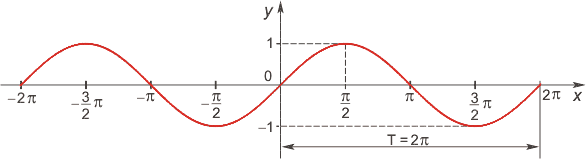
Тригонометрические функции Функция синус

Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2π: sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R. sin x = 0 при x = π·k, k ∈ Z. sin x > 0 (положительная) для всех x ∈ (2π·k, π+2π·k), k ∈ Z. sin x < 0 (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), k ∈ Z. Функция возрастает от −1 до 1 на промежутках: Функция убывает от −1 до 1 на промежутках: Наибольшее значение функции sin x = 1 в точках: Наименьшее значение функции sin x = −1 в точках: