18. Совместная гармоническая и

СТАТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ

При поступлении на вход нелинейного элемента суммы двух сигналов периодического и случайного в виде:

,

можно считать что коэф. статич-ой линеаризации яв-ся периодическими ф-циями времени, то есть имеет вид

(1)

Применив к выражению (5) совместную гармоническую и статическую линеаризацию, получим приблизительную зависимость (2):

где

(3)

(4)

(5)

Представленные формулы показывают, что

, ,представляет собой усредненные за период 2π значения гармонической составляющей передаточной функции и статических коэффициентов.

Коэф. – статич. коэф. усредненный за период 2π

коэф. гармонической линеаризации.

19. Гармоническая линеаризация

ТИПОВЫХ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ

Классическая теория гармон. линеаризации предполагает, что сигналы, снимаемые с выхода нелинейности, является периодическими и имеют основную частоту с частотой синуса входного сигнала. В результате этого допущения, при нахождении эквивалентных передаточных функций или коэффициентов гармонической линеаризации, учитывают только первую гармонику, а влиянием высших корней пренебрегают. Это справедливо для систем, линейная часть которых является низкочастотной и подавляет колебание высоких частот.

Пусть на вход однозначной нелинейности поступает сигнал:

(1), тогда выходной сигнал:

(2)

Введем понятие приближенного значения выходного сигнала:

(3) где А₁ – 1^ая гармоника сигнала на выходе нелинейности.

Запишем выражение (3) через коэф-ты гармонической линеаризации.

(4)

Учитывая выражение (1) перепишем (4)

(5)

, (6) или

(7)

Т.е. получим, что коэф. гармонической линеаризации однозначной нелинейности представляет собой коэффициент усиления, определяемый отношением амплитуды первой гармоники выходного сигнала к гармонике входного сигнала.

Перейдем теперь к аналитич. и гармонич. определению коэф. гармонической линеаризации для двухзначных нелинейных систем. В этом случае при действии на вход нелин. сигнала, записанного в аналит-ом виде, формула (3), на выходе имеем приближенное значение сигнала:

(8)

где – сдвиг фазы, зависящий от величины амплитуды

входного сигнала.

Или (9) где

Пользуясь значением коэф. гармон. линеаризации а(А), в(А) из ур-ия (9) получим:

(10)

Формула для определения вых-ого сигнала в соотв. с (10)

(11)

Эквивалентная передаточная функция

(12)

или

(13)

где

– эквивалентная двухзначная

нелинейность по 1^ой гармонике

Формулы для вычисления гармон. линеаризации наиболее часто встречающихся типов однозначных нечет. Нелинейностей.

а) б)

β

β

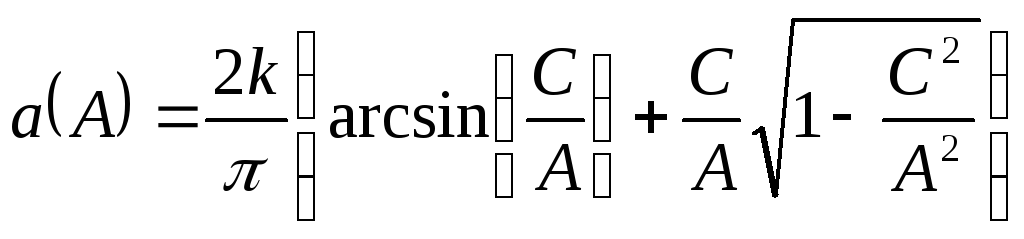
в)

у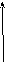

b

– b

– ф-ция Ламмеля

У всех типов однозначной нелинейности

,

тогда по данным нетрудно получить формулы для построения шаблонов с помощью которых находят амплитуды автоколеб. в нелин. САР.

–шаблон фазы амплитуд

Использование полученных ранее формул позволяет получить коэф. гармонической линеаризации 2^ух нелинейностей.

г)

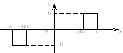д)

Значения для эквивалентной амплитудной и фазовой двухзначной нелинейностей.

При

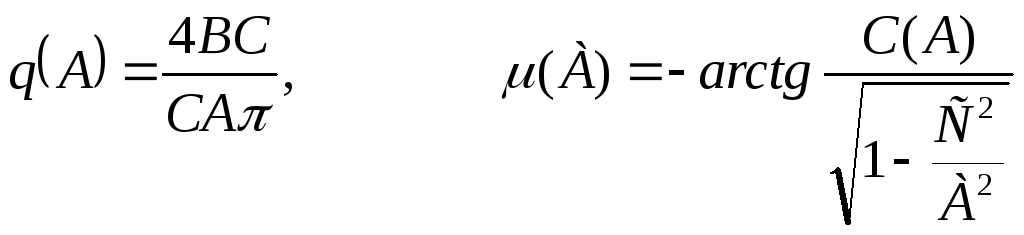
При

х

Для построения шаблонов, рассмотренных нелинейностей, используют формулы:

–для амплитуды

–для фазы

С помощью них находят амплитуды и частоты автоколебаний в нелинейных САР и строят области устойчивых и неустойчивых состояний по параметрам линейной и нелинейной части.

Существует два типа двухзначных нелинейностей: пассивные и активные.

Под пассивными понимаются такие двузначные нелинейности, которые за один период входного сигнала нелинейной характеристики обходится против часовой стрелки. В этом случае в выходном сигнале наблюдается фазовое запаздывание. Если обход нелинейной характеристики проходит по часовой стрелке, то двузначная нелинейность является активной и в выходном сигнале имеет место фазовое опережение.

Активные нелинейности применяют в устройствах коррекции САР для обеспечения устойчивости. Реализация таких устройств может быть выполнена на электронных элементах или в виде рабочей программы.

Рассмотрим гармоническую линеаризацию нелинейности, когда на их вход поступает сигнал вида:

,

где – постоянная составляющая основного сигнала.

Тогда 1^ое приближение выходного сигнала имеет вид:

,

где – функция смещения входного сигнала;

–коэффициент гармонической линеаризации.

Приведем формулу для F(x₀,A), a(x₀,A) для типичных симметричных однозначных нелинейностей.

,

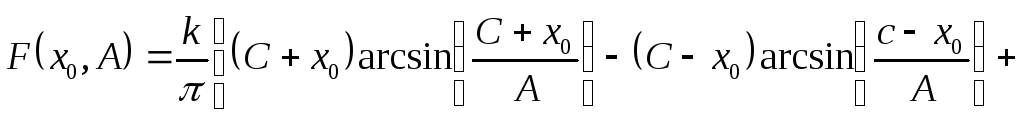
при А ≥ С +‌│х₀│ – для однозначной нелинейности со

смещением.

Для двухзначной нелинейности

,

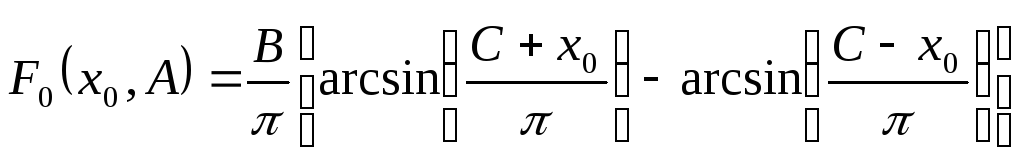
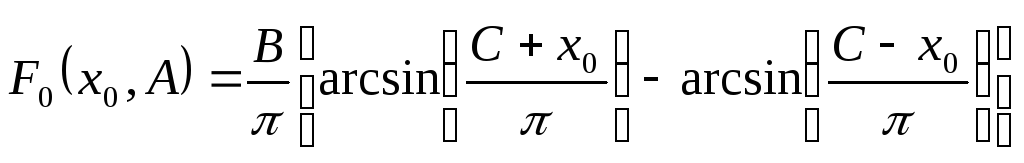
при

В нелинейных системах при недостаточном уровне подавления линейной части высших гармоник, необходимо учитывать дополнительные гармонические составляющие – автоколебания. При этом эквивалентная передаточная функция зависит от двух сигналов: частотного или многочастотного сигналов. Использование таких передаточных функций в нелинейных системах целесообразно, если требуется оценить влияние высших гармоник на появление автоколебаний.

Например: если в системе на первой гармонике открывают автоколебания, а действие третей появится.

Пусть на вход двузначной нечетной нелинейности поступает сигнал:

(106)

где – сдвиг фазы третьей гармоник.

Тогда на выходе

(107)

Пусть ,

(108)

где и– коэффициенты

линеаризации по первой и третьей гармонике.

(109)