
- •Понятие лса. Общие подходы к проектированию
- •Требования, предъявляемые локальным сетям
- •Вид потребляемой энергии Аналоговые локальные системы
- •Математические модели объектов управления
- •Методы линеаризации уравнений
- •Мм нелинейных элементов
- •Общий метод описания эквивалентных передаточных функций нэ
- •Гармоническая линеаризация типовых нелинейных элементов
- •Двузначная нелинейность
- •Для двухзначной нелинейности
- •Статическая линеаризация существенных нелинейных элементов
- •Совместная гармоническая и статическая линеаризация
- •Логарифмические эквивалентные амплитудные и фазовые характеристики сложных нелинейных элементов
- •Статическая линеаризация существенных дискретных нелинейных элементов
- •Вычислительные процедуры для определения коэффициента гармонической и статической линеаризации нелинейных элементов
- •Математическая модель сар
- •Управляемость и наблюдаемость
- •Анализ локальных систем управления
- •Качество
- •Построение переходных процессов с помощью вещественных или мнимых частных характеристик
- •Построение переходных процессов с помощью импульсных переходных систем
- •Исследование динамической точности
- •Коэффициенты ошибок
- •Определение характеристик точности и дискретно-непрерывных лса
- •Синтез лса
- •Синтез линейных непрерывных локальных систем заданных структур
- •Синтез дискретно непрерывных систем
- •Последовательное программирование
- •Параллельное программирование
- •Синтез линейных непрерывных локальных систем
- •Постановка задачи синтеза частотными методами
- •Выбор параметров неизменяемой части
- •Выбор типа двигателя для регулируемого органа
- •Электрические двигатели
- •Гидравлические двигатели
- •Проверка правильности выбора механической передачи
- •Синтез последовательных и параллельных корректирующих устройств
- •Подстановка задачи и выбора универсальной эвм
- •Примеры синтеза систем комбинированного типа
- •Сенсорные устройства. Датчики роботов.
- •Позиционные лсу
- •Контурные лсу
Математические модели объектов управления
Для математической модели наиболее часто применяются дифференциальные, интегрально-дифференциальные уравнения, записанные по координатой или векторно-матричной форме.
Динамические элементы относятся к непрерывным, если рассматриваются в них и сигналы изменяются непрерывно.
В дискретных элементах процессы и системы имеют конечное число значений по величине и времени.
Максимальное описание элементов удобно выполнить через переменные состояния. Они аналогичны обобщенным координатам, а пространство их изменения является фазовым.
Обычно при описании
элементов непрерывного действия
используют
![]() - переменное состояние,
- переменное состояние,![]() - выходной сигнал,
- выходной сигнал,![]() - входной сигнал.
- входной сигнал.
 (5)
(5)

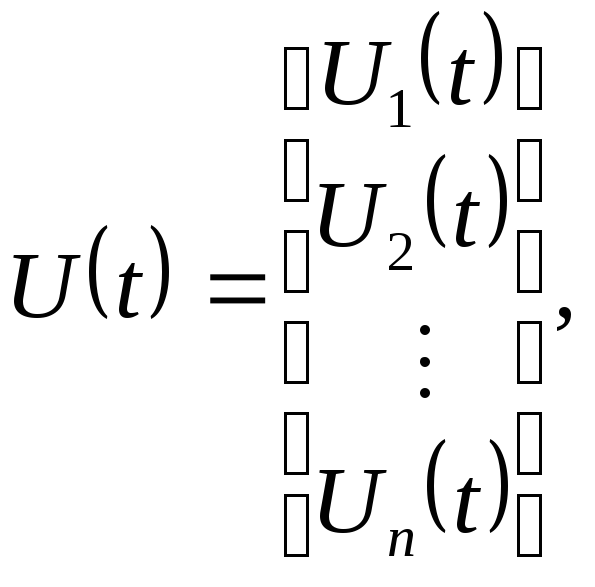
 (6,7,8)
(6,7,8)

 (9,10)
(9,10)
Система (5) справедлива на заданном интервале времени и при заданных начальных условиях.
Система (5) считается
не линейной, если кроме нелинейных
состояний
![]() ,
есть их производные степени и транспортной
функции.
,
есть их производные степени и транспортной
функции.
Пример № 1. Уравнение устройства для замера угловых скоростей на выходе вала двигателя внутреннего сгорания.
![]() ,
(11)
,
(11)
где
![]() - масса устройства,
- масса устройства,
![]() - перемещение
устройства,
- перемещение
устройства,
![]() - коэффициент
скоростного терния,
- коэффициент
скоростного терния,
![]() - коэффициент
жесткости пружины,
- коэффициент
жесткости пружины,
![]() - угловая скорость
выходного вала,
- угловая скорость
выходного вала,
![]() - коэффициент
пропорциональности при угловой скорости.
- коэффициент
пропорциональности при угловой скорости.
Обозначим:
![]() ,
(12)
,
(12)
![]() ,
(13)
,
(13)
получим:
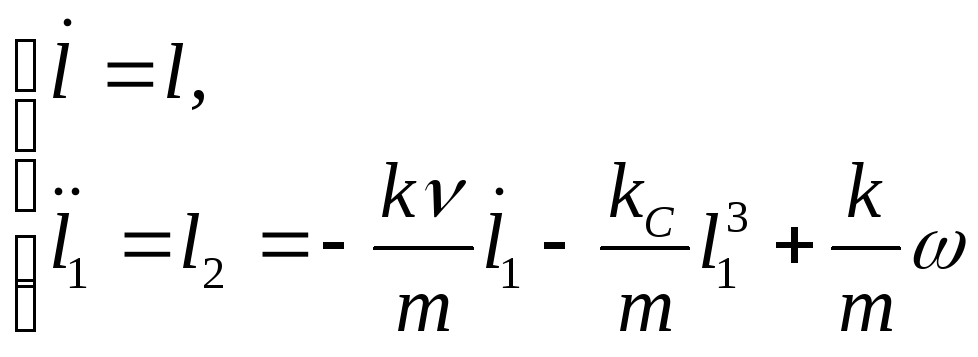 .
(14)
.
(14)
Пример № 2. Уравнение вертикально стартующей вверх ракеты род действием силы тяги двигателя.
![]() ,
(15)
,
(15)
- уравнение не линейное и не стационарное.
где
![]() - высота подъема,
- высота подъема,
![]() - коэффициент
пропорциональности,
- коэффициент
пропорциональности,
![]() - коэффициент
трения,
- коэффициент
трения,
![]() - ускорение
свободного падения.
- ускорение
свободного падения.
Ведем следующие обозначения:
![]() ,
(16)
,
(16)
![]() .
(17)
.
(17)
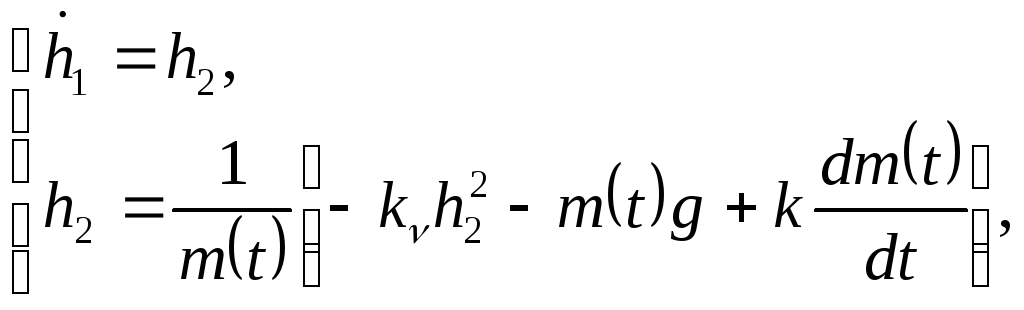
![]() .
.
При описании элементов дискретного действия в общем виде используют уравнения:
 (18)
(18)

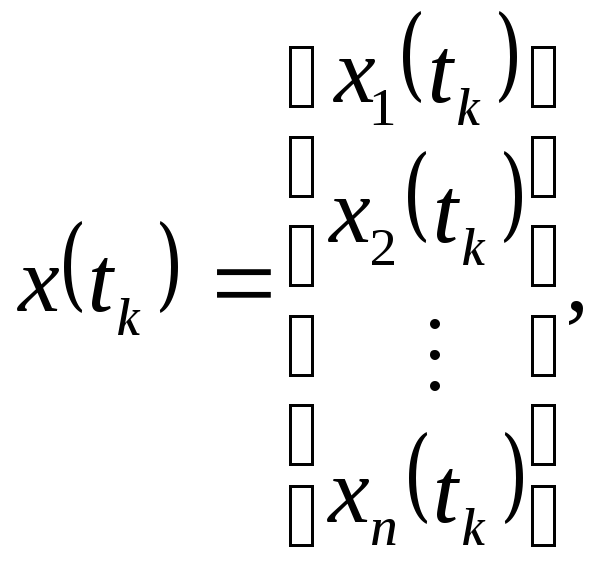
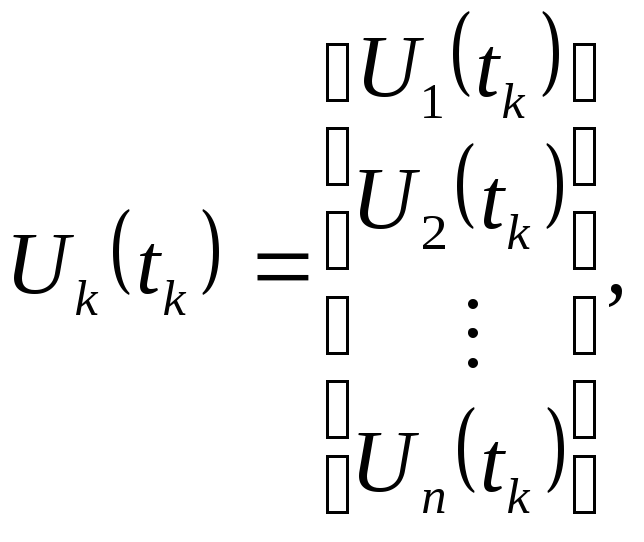 (19,20,21)
(19,20,21)
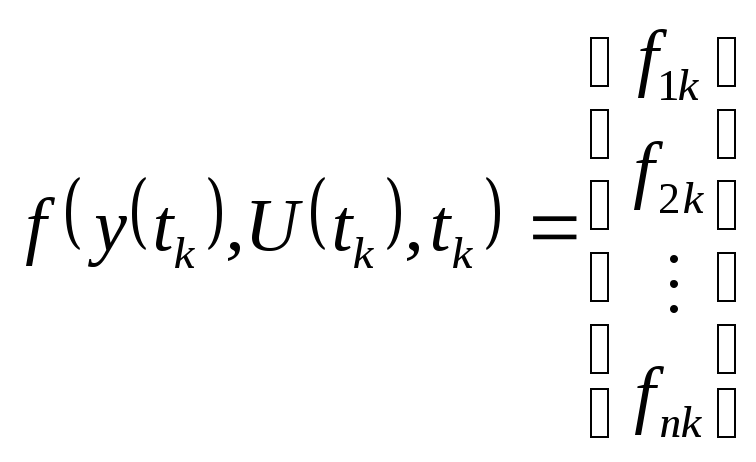 ,
(22)
,
(22)
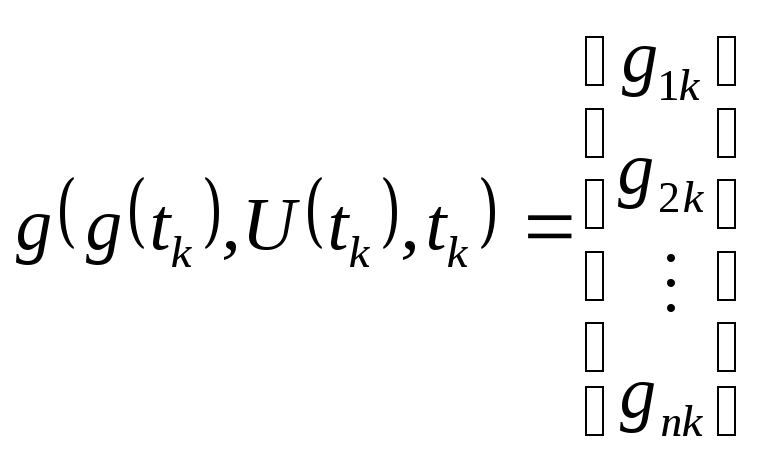 .
(23)
.
(23)
Наиболее
распространенным случаем, является
случай, когда такт квантования равен
постоянному времени
![]() .
.
Тогда уравнение (18) запишется в виде:
 (24)
(24)
Составим разностное уравнение для численных процедур интегрирования и их реакции на управляющей ЭВМ.
Пусть
![]() .
(25)
.
(25)
Начальные условия:
![]() ,
(26)
,
(26)
![]() .
(27)
.
(27)
Для метода Тейлора:
![]() .
(28)
.
(28)
Для метода Адаме-Башворта:
![]() .
(29)
.
(29)
Для метода Адамс-Мультон:
![]() ,
(30)
,
(30)
Уравнения (28), (29) и (30) реализуются в виде рабочих программ на управляющей ЭВМ.
