
- •Понятие лса. Общие подходы к проектированию
- •Требования, предъявляемые локальным сетям
- •Вид потребляемой энергии Аналоговые локальные системы
- •Математические модели объектов управления
- •Методы линеаризации уравнений
- •Мм нелинейных элементов
- •Общий метод описания эквивалентных передаточных функций нэ
- •Гармоническая линеаризация типовых нелинейных элементов
- •Двузначная нелинейность
- •Для двухзначной нелинейности
- •Статическая линеаризация существенных нелинейных элементов
- •Совместная гармоническая и статическая линеаризация
- •Логарифмические эквивалентные амплитудные и фазовые характеристики сложных нелинейных элементов
- •Статическая линеаризация существенных дискретных нелинейных элементов
- •Вычислительные процедуры для определения коэффициента гармонической и статической линеаризации нелинейных элементов
- •Математическая модель сар
- •Управляемость и наблюдаемость
- •Анализ локальных систем управления
- •Качество
- •Построение переходных процессов с помощью вещественных или мнимых частных характеристик
- •Построение переходных процессов с помощью импульсных переходных систем
- •Исследование динамической точности
- •Коэффициенты ошибок
- •Определение характеристик точности и дискретно-непрерывных лса
- •Синтез лса
- •Синтез линейных непрерывных локальных систем заданных структур
- •Синтез дискретно непрерывных систем
- •Последовательное программирование
- •Параллельное программирование
- •Синтез линейных непрерывных локальных систем
- •Постановка задачи синтеза частотными методами
- •Выбор параметров неизменяемой части
- •Выбор типа двигателя для регулируемого органа
- •Электрические двигатели
- •Гидравлические двигатели
- •Проверка правильности выбора механической передачи
- •Синтез последовательных и параллельных корректирующих устройств
- •Подстановка задачи и выбора универсальной эвм
- •Примеры синтеза систем комбинированного типа
- •Сенсорные устройства. Датчики роботов.
- •Позиционные лсу
- •Контурные лсу
Анализ локальных систем управления
Анализ системы включает три основных этапа:
1. Исследование устойчивости системы.
2. Исследование качества системы.
3. Исследование динамической точности системы.
1) Устойчивость линейных систем по Ляпунову.
2) Устойчивость по Гурвицу.
3) Устойчивость по Раусу.
4) Устойчивость по Венору-Шупору.
5) Устойчивость по Шуркону.
6) Устойчивость по Михайлову.
7) Устойчивость по Найквисту.
8) Устойчивость по D-разбиению.
Качество
При анализе по оценкам качества рекомендуется прибегать к косвенным методам получения таких показателей, позволяющим оценить изменение параметров замкнутой системы. Однако для окончательности решения правильности выбора элементной базы системы, применяют прямые методы, связанные с построением переходных процессов. На практике пользуются лишь основными показателями качества.
Максимальное отклонение регулируемой величины. Значение максимального перерегулирования, время протекания переходного процесса, время нахождения первого максимума, число колебаний, максимальная скорость обработки регулируемой переменной.
Используются интегральные оценки качества. Они являются обобщенными показателями, позволяющие по переходной динамической составляющей ошибки системы исследовать характер протекания переходного процесса.
![]() ,
(139)
,
(139)
![]() ,
(140)
,
(140)
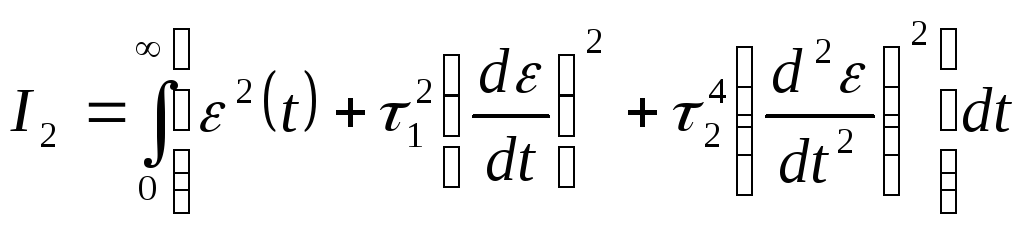 ,
(141)
,
(141)
![]()
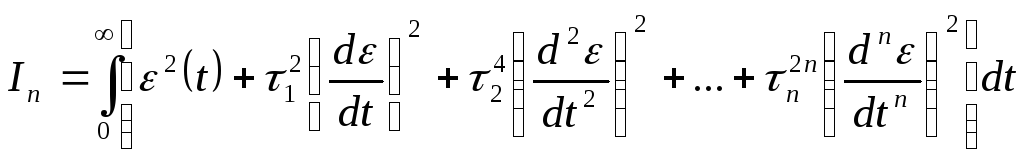 .
(142)
.
(142)
Метод корневого годографа.
Для предварительной оценки качества системы, проектировщик должен знать картину перемещения полюсов и нулей в замкнутой системе, в зависимости от изменения ее основных параметров.
Корневой годограф – это геометрическое место точек, для которого выполняется условие:
![]() ,
(143)
,
(143)
![]() ,
(144)
,
(144)
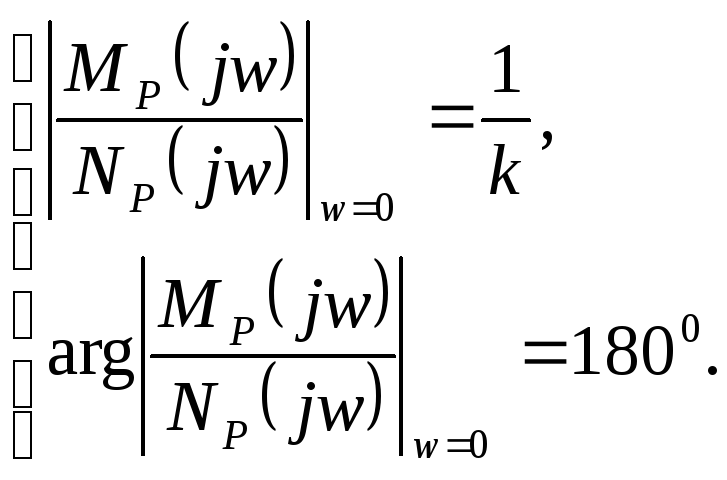 (145)
(145)
Под корневым годографом понимают движение корней в комплексной плоскости с помощью уравнения замкнутой системы.
Построение переходных процессов с помощью вещественных или мнимых частных характеристик
- приводит с помощью обратного преобразования Лапласа.
![]() ,
(146)
,
(146)
при
![]() ,
,
где
![]() - абсцисса абсолютной сходимости функции
- абсцисса абсолютной сходимости функции![]() .
.
![]() ,
(147)
,
(147)
где
![]() - регулярная часть, содержащая все полюса
функции
- регулярная часть, содержащая все полюса
функции![]() в левой полуплоскости;
в левой полуплоскости;
![]() - регулярная часть,
содержащая все функции в правой
полуплоскости.
- регулярная часть,
содержащая все функции в правой
полуплоскости.
![]() (148)
(148)
или
![]() ,
(149)
,
(149)
![]() ,
(150)
,
(150)
![]() .
(151)
.
(151)
Располагая части
регулярной системы, можно найти
соответствующие
![]() по формулам решения дифференциальных
уравнений, вычислением произвольных
состояний.
по формулам решения дифференциальных
уравнений, вычислением произвольных
состояний.
