Задача 5

5.1 Постановка задачі

Припустимо, що тривалість життя описується моделлю де Муавра з граничним віком  = 80 + №В років, а процентна ставка дорівнює (5 + 0,5*№В) %. Підрахуйте нетто-премію для людини у віці 30 + №В, якщо укладено договір:

а) повного страхування життя;

б) 10-річного страхування життя;

в) 10-річного змішаного страхування життя;

г) повного страхування життя, відстроченого на 5 років;

д) повного страхування життя з неперервно зростаючою страховою виплатою.

5.2 Хід виконання задачі та висновки

Перш ніж приступимо до розв’язку задачі, розглянемо теоретичні основи моделі де Муавра.

Нетто-премія для моделі де Муавра ( – процентна ставка, S₀ – сума грошей у початковий момент часу (t = 0)).

. (5.1)

N-річне страхування життя. Страховик виплачує страхувальникові b грн., якщо він помирає, не доживши до n років, і не виплачує нічого, якщо він проживає n років.

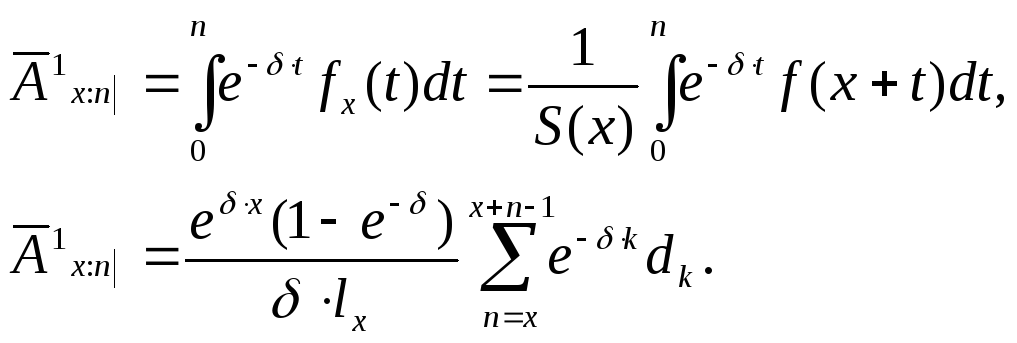(5.2)

N-річне змішане страхування життя. Договір укладається на n років, виплати здійснюються або в момент смерті застрахованого, або після закінчення n років, якщо застрахований не помре.

Повне страхування життя, відстрочене на m років. Страхова виплата здійснюється тільки у випадку, коли страхувальник помирає пізніше m-річного терміну.

Нетто-премія такого договору:

(5.3)

Повне страхування життя з неперервно зростаючою страховою виплатою. У момент смерті страхувальникові виплачується Т(х) одиниць.

Нетто-премія такого договору:

(5.4)

Перейдемо безпосередньо до розв’язку даної задачі.

Першим кроком водимо дані:

(5.5)

де В- номер варіанту;

ω - роки життя;

І - процентна ставка;

η - інтенсивність відсотків;

А- вік людини;

υ – коефіцієнт дисконтування.

Наступним етапом ми розраховували повне страхування життя, за формулою(5.2), яку можна записати в двох варіантах:

(5.6)

(5.7)

Відповідно до даних формул отримали результати відповідно:

(5.8)

(5.9)

Отже повне страхування життя становить – 0.011*100% = 1.1%.

Далі проводимо розрахунки 10-річного страхування життя, за формулами:

(5.10)

(5.11)

За даними формулами отримали значення:

(5.12)

Отже 10-річноне страхування життя дорівнює – 0.011*100% = 1.1%.

Далі знайдемо повне страхування життя, яке відстроченого на 5 років, за формулою:

(5.13)

Отримали значення:

(5.14)

Отриманий розрахунок запишемо у відсотковому відношенні, яке становить - (9,209/10000000)*100% = 0.00009209%.

Останнім етапом розрахунку даної задачі є розрахунок повного страхування життя з неперервно зростаючою страховою виплатою, яке здійснюється за формулою:

(5.15)

За даною формулою отримали розрахунок:

(5.16)

Запишемо отриманий результат у відсотковому відношенні - (5,708/1000)*100%=0,5708%.

На основі отриманих нетто - премій, можна сказати, що отримані числа є дуже маленькими, а отже модель Муавра можна вважати дуже грубою. Реально її можна використовувати для апроксимації функції виживання на певному інтервалі часу.