1.2. Алгоритмы

Алгоритм – это заранее заданная последовательность четко определенных правил или команд для получения решения за конечное число шагов. Основные свойства алгоритма:

- вход алгоритма;

- выход алгоритма;

- определенность его шагов;

- выполнимость;

- конечность;

- эффективность;

- универсальность;

- элегантность.

Определенность его шагов – инструкция должна быть определена четко и недвусмысленно. Например, инструкция:

если 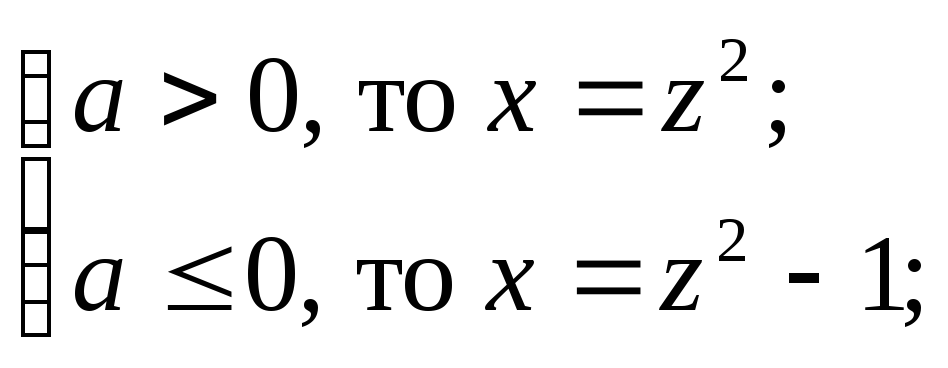является определенной, а инструкция:

если 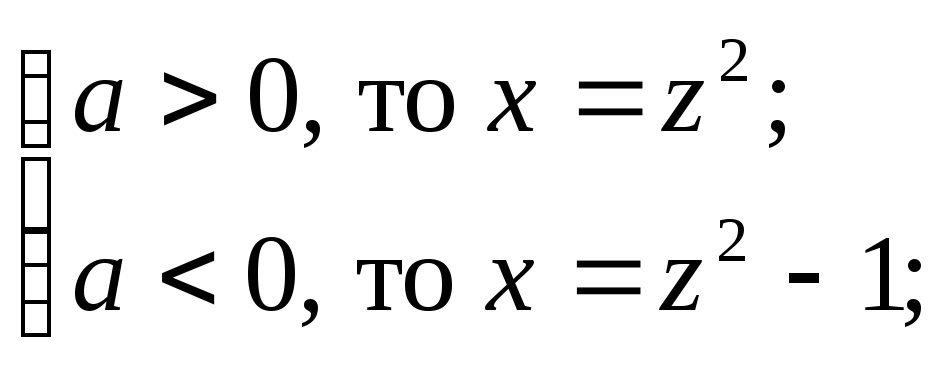не определена при .

6

Выполнимость – алгоритм выполним, если включенные в

него операции достаточно элементарны, чтобы их за конечное время мог выполнить человек, вооруженный карандашом и бумагой. То, что простота, с которой написана инструкция, не определяет его выполнимость видно из следующего примера: присвоить значение, равное наибольшему вещественному числу, меньшему единицы. Эту инструкцию выполнить невозможно потому что, какое бы значение мы не выбрали, всегда можно указать число, большее выбранного путем добавления любой цифры к десятичной записи числа: .

Конечность – алгоритм заканчивается за конечное число шагов. Пример бесконечного алгоритма:

;

;

.

Эффективность – алгоритм будет эффективным, если он производит вычисления максимально быстро и использует при этом минимально возможный объем памяти. Сочетание этих двух требований является противоречивым. Эффективность оценивается по отношению к другим алгоритмам, по отношению к ресурсам и никогда не бывает абсолютной.

Нельзя использовать первый пришедший в голову алгоритм, не рассмотрев альтернативных вариантов. Например, необходимо найти сумму первых натуральных чисел. Алгоритм решения этой задачи может быть представлен так:

Более внимательное рассмотрение приводит к выводу, что натуральный ряд является арифметической прогрессией, и

7

сумма членов этого ряда может быть определена по формуле: .

Универсальность – способность алгоритма решать широкий класс задач. Критерий универсальности и критерий эффективности противоречивы. Алгоритм для решения конкретной задачи может выиграть за счет особенностей данной задачи и быть эффективным, а универсальность снижает эффективность.

Элегантность – весьма субъективное понятие. Элегантное решение – это сочетание простоты и оригинальности. Под оригинальностью понимается его неочевидность. Например, поменять значения двух переменных можно без копирования, воспользовавшись следующим алгоритмом:

Ниже приведено содержание ячеек памяти, соответствующее каждому шагу алгоритма:

Начальное состояние:

Шаг 1.

Шаг 2.

Шаг 3.

Способы записи алгоритмов. Для записи алгоритмов можно воспользоваться следующими способами:

1. Запись алгоритмов на естественном языке.

2. Использование псевдокода (полуформального языка с ограниченным словарем, промежуточного между естественным языком и языком программирования). Псевдокод удобен тем, что позволяет программисту сосредоточиться на формулировке алгоритма, не задумываясь над синтаксическими особенностями конкретного языка программирования.

8

3. Запись алгоритма в виде структурной схемы. Для этого

используются специальные графические символы, подробное описание которых можно найти в [3].

Рассмотрим примеры разработки алгоритмов для решения следующих задач.

Задача 1. Разработать алгоритм для нахождения суммы членов бесконечного ряда

.

Суммирование прекращать, если абсолютная величина очередного члена ряда станет меньше заданной погрешности .

Решение. В качестве входных переменных будут выступать значение и заданная погрешность . Задачу можно разбить на ряд самостоятельных подзадач. Первая подзадача – это возведение числа в заданную целочисленную степень , то есть умножение само на себя раз. Вторая подзадача – нахождение , то есть вычисление по формуле .

Определим начальные значения переменных и : в качестве начального значения суммы целесообразно взять значение первого члена ряда (), а начальному номеру очередного суммируемого члена придать значение 1 ().

Тогда обобщенный алгоритм решения этой задачи будет выглядеть так:

1. Задать значения 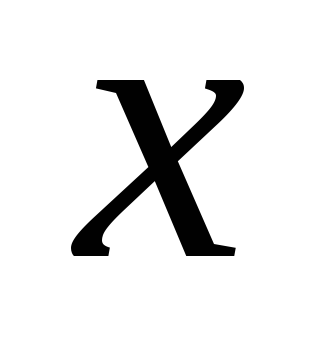и

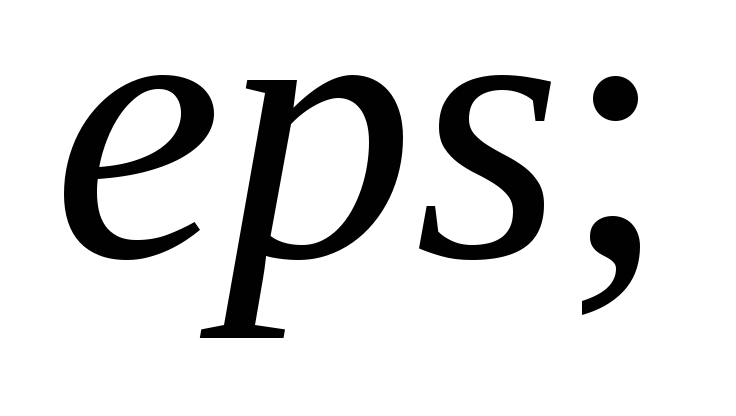
2. Установить начальные значения: 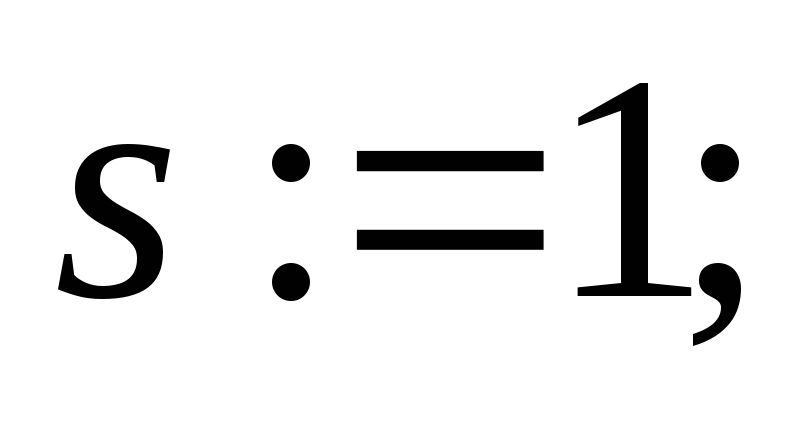и

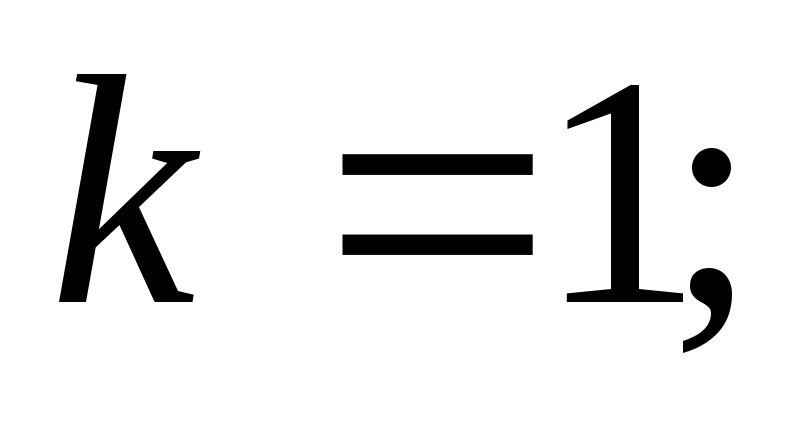
3. Вычислить значение

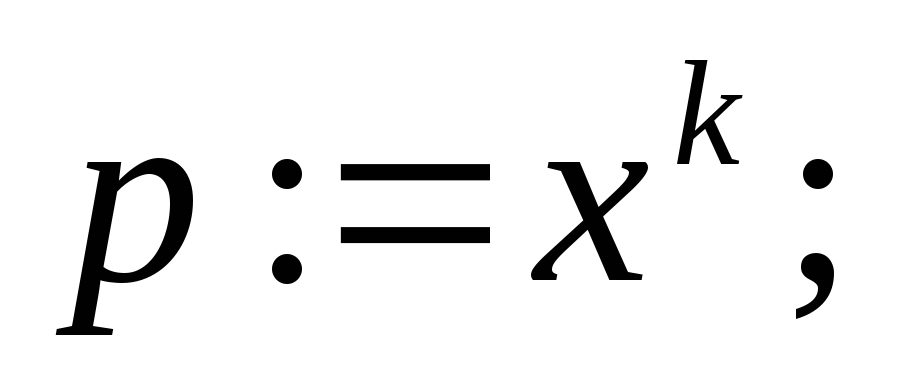
4. Вычислить значение

5. Вычислить значение очередного члена ряда

9

6. Если , то перейти к шагу 7. В противном случае перейти к шагу 8;

7. ; ; перейти к шагу 3;

8. Вывести значение ;

Детализируем алгоритм вычисления (шаг 3).

3.1. Задать начальные значения переменным ;

3.2. Вычислить ;

3.3. Если . Перейти к шагу 3.2. В противном случае перейти к шагу 4;

Детализируем алгоритм вычисления (шаг 4).

4.1. Задать начальные значения переменным ;

4.2. Вычислить ;

4.3. Если . Перейти к шагу 4.2. В противном случае перейти к шагу 5.

Полный алгоритм решения задачи будет выглядеть так:

1. Задать значения 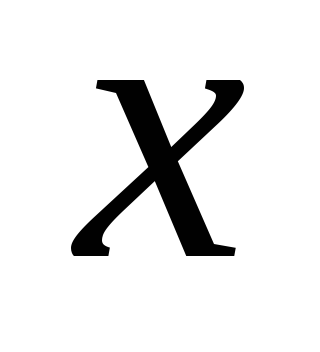и ;

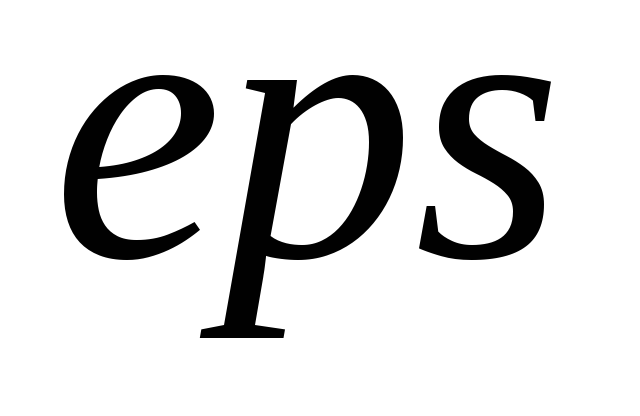2. Установить начальные значения: и ;

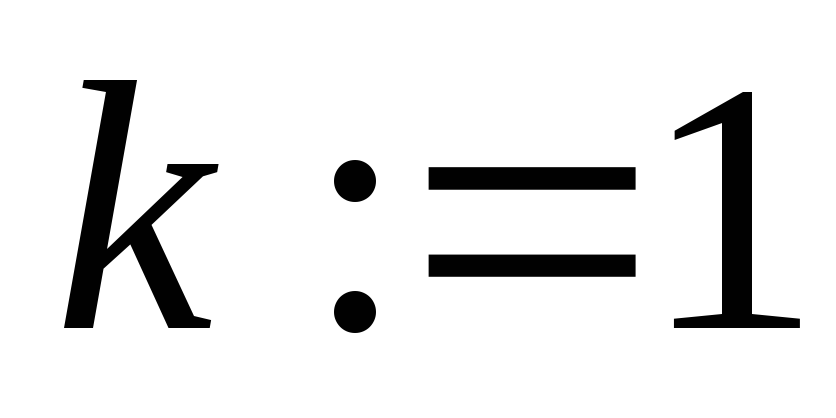3. Вычислить значение ;

3.1. Задать начальные значения переменным ;

3.2. Вычислить ;

3.3. Если . Перейти к шагу 3.2. В противном случае перейти к шагу 4;

4. Вычислить значение ;

4.1. Задать начальные значения переменным ;

4.2. Вычислить ;

4.3. Если . Перейти к шагу 4.2.

10

В противном случае перейти к шагу 5.

5. Вычислить значение очередного члена ряда ;

6. Если , то перейти к шагу 7. В противном случае перейти к шагу 8;

7. ; ; перейти к шагу 3;

8. Вывести значение ;

Задача 2. Дано натуральное число . Сколько цифр в числе ?

Для подсчета количества цифр в числе необходимо целочисленно разделить данное число на 10, полученный результат снова разделить на 10 и так до тех пор, пока результат целочисленного деления не станет равным нулю.

Алгоритм решения этой задачи будет выглядеть так:

1. Задать исходное число ;

2. Установить начальное значение счетчика количества цифр в числе, равным нулю;

3. Найти результат целочисленного деления на 10: ;

4. Если , то ; . Перейти к шагу 3. В противном случае перейти к шагу 5.

5. Вывести значение .

Контрольные вопросы и упражнения

1. Перечислите основные этапы разработки программы и охарактеризуйте каждый из них.

2. Перечислите основные свойства алгоритма и дайте пояснения по каждому из них.

3. Дайте характеристику способам записи алгоритмов.

4. Для следующих задач разработать алгоритм решения и представить его в виде структурной схемы:

11

4.1. Треугольник задан координатами своих вершин. Найти периметр треугольника и его площадь.

4.2. Даны три произвольных числа. Определить, можно ли построить треугольник с такими длинами сторон.

4.3. Определить, равен ли квадрат заданного трехзначного числа кубу суммы цифр этого числа.

4.4. Дано натуральное число . Выяснить входит ли цифра 3 в запись числа .

4.5. Даны целые числа . Вычислить .

4.6. Дано натуральное число . Вычислить .

4.7. Дано натуральное число . Определить, чему равна сумма цифр в числе .

4.8. Дано натуральное число . Вычислить произведение первых сомножителей: .

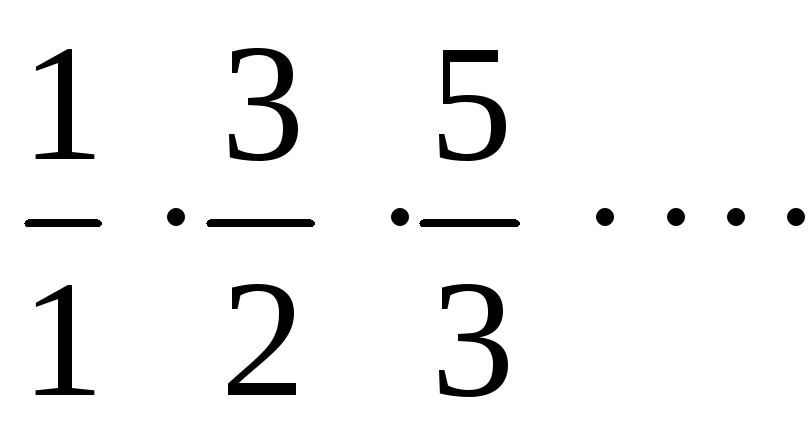4.9. Дано действительное число . Вычислить .

4.10. Дано натуральное число и действительное число . Вычислить:

.

4.11. Дано натуральное число k. Найти k-ую цифру последовательности, в которой идут подряд квадраты всех натуральных чисел. Последовательность предварительно не формировать.

4.12. Автобусные билеты пронумерованы от 000001 до

999999. Найти номера всех счастливых билетов в заданном диапазоне.

12

4.13. Куб любого натурального числа равен сумме нечетных чисел, следующих по порядку за числами, сумма которых составила куб числа :

,

,

,

,

.

Основываясь на этом свойстве, разработать алгоритм получения таблицы кубов натуральных чисел.

4.14. В книге страниц. Определить, сколько цифр потребуется для нумерации всех страниц этой книги.

4.15. Для нумерации страниц книги потребовалось цифр. Определить количество страниц в книге.

4.16. Дано целое число . Записываем это число в двоичной системе счисления и циклически сдвигаем вправо, то есть, берем последнюю цифру числа и переносим ее в начало. Для заданного числа определить максимальное значение числа, которое получится в результате таких сдвигов.

4.17. Разработать алгоритм перевода числа из десятичной системы в системы счисления с основаниями 3 и 5.

4.18. Найти все трехзначные числа, в десятичной записи которых нет одинаковых цифр. Найденные трехзначные числа расположить в порядке возрастания.

4.19. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа.

4.20. Определить, является ли заданное натуральное число палиндромом, то есть таким, десятичная запись которого читается одинаково слева направо и справа налево.

13

ЗАНЯТИЕ 2. ТИПЫ ПЕРЕМЕННЫХ В TURBO PASCAL