5.4. Рекурсивные процедуры и функции
Рекурсивным называется объект, частично определяемый через самого себя, например:
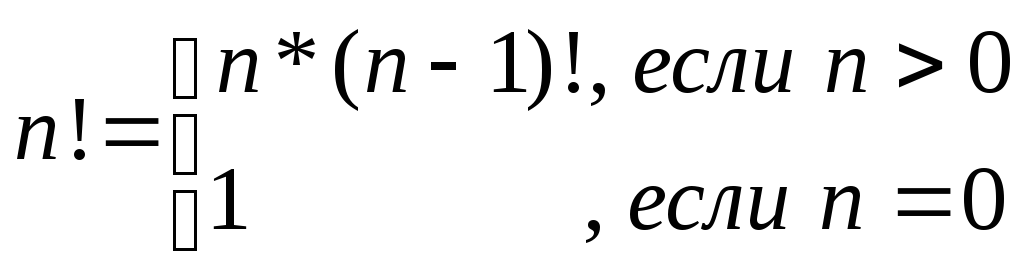
Рекурсия
в программировании
– это способ организации программ, при
котором подпрограмма прямо или косвенно
вызывает саму себя. Если подпрограмма
вызывает себя в своем теле, то такая
рекурсия называется прямой.
Если же подпрограмма
вызывает подпрограмму
,
которая прямо или косвенно вызывает
,
то такая рекурсия называется косвенной.
Любая рекурсивная подпрограмма должна содержать два обязательных элемента:
- условие завершения, в противном случае процесс рекурсивного обращения будет бесконечным;
87
- способ выражения одного шага решения посредством другого, более простого шага.
Проиллюстрируем механизм рекурсии на примере вычисления факториала числа.
Function fact(n: integer): real;
begin
if n = 1 then fact: = 1 {Условие завершения рекурсии}
else
fact:
= n
* fact(n-1)
{Происходит рекурсивное} {обращение к
функции , но уже с меньшим значением
}
end;
Рассмотрим более подробно вычисление fact(5).
На
первом шаге
,
поэтому происходит повторное обращение
к функции уже со значением
,
затем со значением
и так далее, пока
не станет равным 1, то есть, не будет
достигнуто условие, позволяющее
организовать своевременную остановку
процесса. Процесс рекурсивных вызовов
называется рекурсивным
спуском.
Процесс
возврата из рекурсивных вызовов,
наступающий после получения
называется рекурсивным
возвратом.
;
Но
для выполнения рекурсивного возврата
необходимо одновременно хранить в стеке
в течение всего времени работы функции
коэффициенты:
.
Если
значение
достаточно велико, то возможно переполнение
стека и аварийное завершение программы.
Рассмотрим
функцию, реализующую возведение целого
числа
в целую неотрицательную степень
:
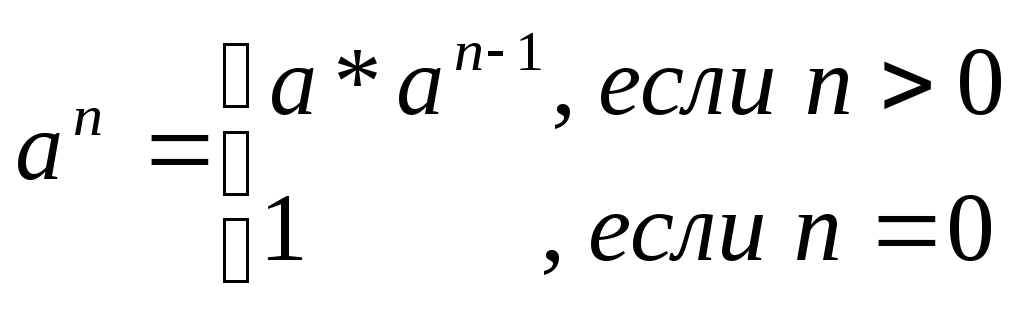
88
Function Power (a, n : integer): real;
begin
if n = 0 then power: =1
else
begin
if odd(n) then power: = a*power(a, n-1)
{Если
показатель степени будет четным, то
можно сократить} {число обращений,
использовав зависимость
}
else power: = power(a*a, n div 2);
end;
end;
Используем рекурсию для нахождения минимального элемента в одномерном массиве:
type mas=array[1..10] of real;
var n: integer;
a: mas;
function minX(const x: mas; n: integer): real;
var result: real; i: integer;
begin
write(n,' - ');
for i:=1 to n do
write(x[i]:3:0, ' ');
writeln;
if n = 1 then result: = x[n]
else
begin
result: =minX(x,n-1);
writeln('x[n] result');
writeln(x[n]:3:0, ' ',result:3:0);
if x[n] < result then result: = x[n];
89
end;
minX: = result;
end;
begin
n: = 5;
a[1]: = 23; a[2]: = 10; a[3]: = 85;
a[4]: = 3; a[5]: = 16;
writeln(minX(a,n));
end.
Механизм работы программы иллюстрируется следующим протоколом:
5 - 23 10 85 3 16
4 - 23 10 85 3
3 - 23 10 85
2 - 23 10
1 - 23
x[n] result
10 23
85 10
3 10
16 3
3
Рекурсивные подпрограммы чаще всего применяют для компактной записи рекурсивных по своей природе алгоритмов, а также для работы со структурами данных, которые определяются в терминах рекурсии. Любую рекурсивную подпрограмму можно реализовать без применения рекурсии.
Достоинством рекурсии является компактная запись. К недостаткам относятся: расход времени и памяти на повторные вызовы функции и передачу ей параметров, а также возможность переполнения стека.
90
Контрольные вопросы и упражнения
1. Чем отличаются процедуры от функций?
2. Чем отличаются формальные параметры от фактических?
3. В чем различие между параметрами-значениями и параметрами переменными?
4. Какие обязательные элементы должны содержать рекурсивные процедуры и функции?
5. Что такое рекурсивный спуск и рекурсивный возврат?
Разработать программы для решения следующих задач:
6.
Построить матрицу
,
где
- квадратные матрицы,
-
единичная матрица.
Ввод
матриц, вывод матриц на экран и
формирование матрицы
оформить в виде подпрограмм.
7.
Получить
,
где
- квадратные матрицы,
-
натуральное число.
Ввод
матриц, вывод матриц на экран и
формирование матрицы
оформить в виде подпрограмм.
8. Даны три целочисленные квадратные матрицы. Найти ту из них, где больше нулевых строк.
Ввод матриц, вывод матриц на экран, поиск нулевых строк оформить в виде подпрограмм.
9.
По вещественным числам
и
вычислить с точностью
величину:
.
Для вычисления корней использовать следующий ряд Тейлора:
91
,
где
,
.
Вычисление корней оформить в виде процедуры или функции.
10. Разработать
программу для умножения симметричных
матриц на n-мерный вектор. Матрица
-
го порядка задана:
а) верхним треугольником;
б) одномерным вектором, полученным из представления симметричной матрицы в виде верхнего треугольника, путем построчной записи.
Ввод матриц, вывод матриц на экран, нахождение произведения оформить в виде подпрограмм.
11. Составить программу, подсчитывающую число сочетаний с повторениями, применив формулу
.
Проверить
работоспособность программы при
возрастающих значениях
и
.
Использовать подпрограммы.
-
По вещественному числу
вычислить величину
;
Корни
вычислить с точностью
по итерационной формуле:
Вычисления
производить до тех пор, пока
.
92
13.
По заданным вещественным векторам
размерности
вычислить:
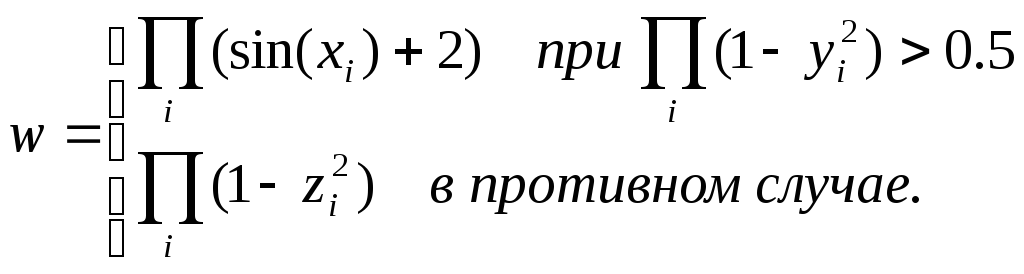
Использовать подпрограммы.
14.
Среди простых чисел, не превышающих
,
найти такие, в двоичной записи которых
максимальное число единиц. Оформить в
виде отдельных подпрограмм процесс
представления числа в двоичной системе
счисления и подсчета количества единиц
в двоичном представлении.
15. Разработать программу для перевода целых чисел из десятичной системы счисления в троичную и пятеричную. Перевод оформить в виде подпрограмм.
16.
Напечатать все цифры десятичной записи
числа
,
представив ”длинные” натуральные
числа в виде массивов из цифр и реализовав
нужные операции над ними. Использовать
подпрограммы.
17.
Напечатать все цифры десятичной записи
числа
,
представив ”длинные” натуральные
числа в виде массивов из цифр и реализовав
нужные операции над ними. Использовать
подпрограммы.
18. Решить задачу 17, разбивая длинные числа не на отдельные цифры, а на группы цифр по 5 цифр.
19. Решить задачу 17, разбивая длинные числа не на отдельные цифры, а на группы цифр по 10 цифр.
93
20.
Разработать программу, которая по
заданным
элементным
массивам
и
вычисляет:
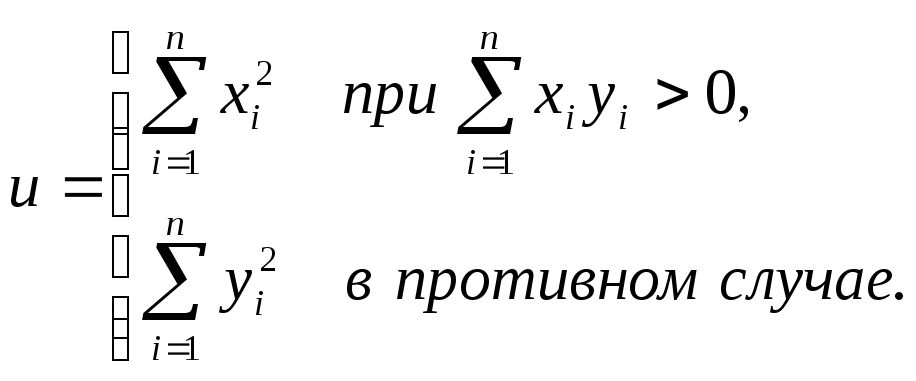
21.
Разработать программу, которая по
заданным
элементным
массивам
,
,
вычисляет:
22.
Разработать рекурсивную и нерекурсивную
процедуру или функцию для нахождения
-
го числа Фибоначчи. Числа Фибоначчи
определяются рекуррентными соотношениями:
.
Установите, сколько вызовов функции
понадобится при
.
Сколько будет вызовов, дублирующих
раннее осуществленные.
23.
Разработать рекурсивную и нерекурсивную
подпрограммы от вещественного
и целого
,
которые вычисляют величину
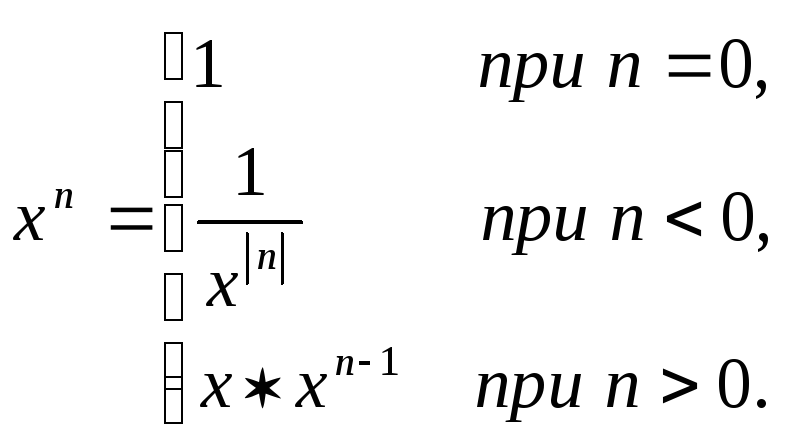
24.
Разработать рекурсивную и нерекурсивную
подпрограммы для вычисления биномиального
коэффициента
по следующей формуле:
94
.
25.
Разработать рекурсивную логическую
функцию, проверяющую, является ли
симметричной часть строки
,
начинающаяся
- м и кончающаяся
-
м ее элементами.
26. Разработайте рекурсивный и нерекурсивный варианты процедуры обращения строки.
27.
Разработайте рекурсивную процедуру
или функцию, которая находит наибольший
общий делитель (НОД) двух натуральных
чисел
и
.
Для решения задачи воспользоваться
свойствами НОД:
ЗАНЯТИЕ 6. МОДУЛИ