5. Ускорение.

Ускоре́ние — производная скорости по времени, векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления). Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².

Единицей ускорения служит метр в секунду за секунду.

Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы: Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.

6. Движение с постоянным ускорением. Единица ускорения.

Единицей ускорения служит метр в секунду за секунду.

Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы: Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.

7. Скорость при движении с постоянным ускорением

Прямолинейное движение с постоянным ускорением называют равноускоренным, если модуль скорости увеличивается со временем, или равнозамедленным, если он уменьшается.

Примером ускоренного движения может быть падение цветочного горшка с балкона невысокого дома. В начале падения скорость горшка равна нулю, но за несколько секунд она успевает вырасти до десятков м/с. Примером замедленного движения является движение камня, брошенного вертикально вверх, скорость которого сначала большая, но потом постепенно уменьшается до нуля в верхней точке траектории. Если пренебречь силой сопротивления воздуха, то ускорение в обоих этих случаях будет одинаково и равно ускорению свободного падения, которое всегда направлено вертикально вниз, обозначается буквой g и равно примерно 9,8 м/с2.

Ускорение свободного падения, g вызвано силой притяжения Земли. Эта сила ускоряет все тела, движущиеся по направлению к земле, и замедляет те, которые движутся от неё.

Чтобы найти уравнение для скорости при прямолинейном движении с постоянным ускорением, будем считать, что в момент времени t=0 тело имело начальную скорость v0. Так как ускорение a постоянно, то для любого момента времени t справедливо следующее уравнение:

где v – скорость тела в момент времени t, откуда после нетрудных преобразований получаем уравнение для скорости при движении с постоянным ускорением: v = v0 + at

8. Уравнения движения с постоянным ускорением.

Чтобы найти уравнение для скорости при прямолинейном движении с постоянным ускорением, будем считать, что в момент времени t=0 тело имело начальную скорость v0. Так как ускорение a постоянно, то для любого момента времени t справедливо следующее уравнение:

где v – скорость тела в момент времени t, откуда после нетрудных преобразований получаем уравнение для скорости при движении с постоянным ускорением: v = v0 + at

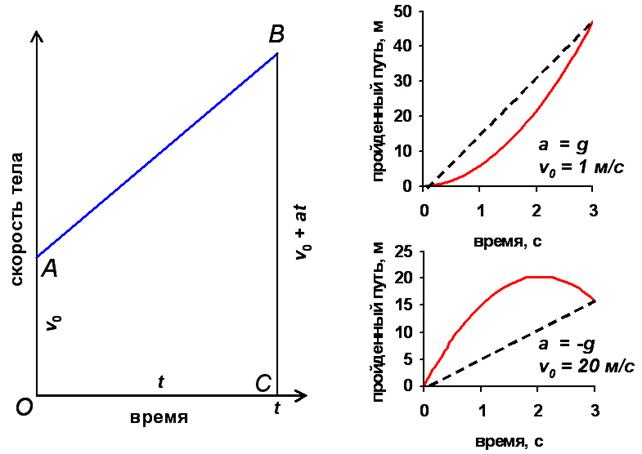
Чтобы вывести уравнение для пути, пройденного при прямолинейном движении с постоянным ускорением, построим сначала график зависимости скорости от времени (5.1). Для a>0 график этой зависимости изображён слева на рис.5 (синяя прямая). Как мы установили в §3, перемещение, совершённое за время t, можно определить, если вычислить площадь под кривой зависимости скорости от времени между моментами t=0 и t. В нашем случае фигура под кривой, ограниченная двумя вертикальными линиями t=0 и t, представляет собой трапецию OABC, площадь которой S, как известно, равна произведению полусуммы длин оснований OA и CB на высоту OC:

Как видно на рис.5, OA = v0, CB= v0 + at, а OC = t. Подставляя эти значения в (5.2), получаем следующее уравнение для перемещения S, совершённого за время t при прямолинейном движении с постоянным ускорением a при начальной скорости v0 :

Легко показать, что формула (5.3) справедлива не только для движения с ускорением a>0, для которого она была выведена, но и в тех случаях, когда a<0. На рис.5 справа красными линиями показаны графики зависимости S при положительных (верх) и отрицательных (низ) значениях a, построенные по формуле (5.3) для различных величин v0. Видно, что в отличие от равномерного движения (см. рис. 3), график зависимости перемещения от времени является параболой, а не прямой, показанной для сравнения пунктирной линией.