Аналоговые
Механические
Пневматические
Гидравлические
Электрические
Электронные
Комбинированные
Общие понятия ЛСУ
Классификация ЛС
ЛСУ
Дискретные
|
|
|
|
|
|
|
|
|
|
|
|
С жесткой логикой |
|
|
Программно- |
||
|
|
|
|
управляемые |
|
|
|
|
|
|
|
Электронные
Пневматические
Электро-механические
Электро-пневмо- гидравлические
Комбинированные
Аналого-дискретные
Дискретно- аналоговые
Аналого-дискретно- аналоговые
Дискретно-аналого- дискретные
1
Общие требования к ЛС
Энергоёмкость.
Вид потребляемой энергии. Надёжность работы.
Быстродействие.
Точность поддержания регулируемого параметра (не более 20%).
Вид системы (дискретная – человек управляет). Элементная база.
Влияние внешних возмущений.
Дизайн.
Это одностороннее регулирование
Nш |
m0c gh |
быстродействие |
|
t |
одностороннего |
||
|
|||
h |
|
регулирования. |
|
|
|
где Nш – работа шара.
mc
2
Рассмотрим процесс двустороннего регулирования:
h
mcg |
|
|
|
|
|
mc |
(мешки с |
|
|
|
|
|
(пассажиры) |
|
|
|
|
|
||
песком) |
|
|
|
|
|
|
m |
|
N ш |
||||
t |
gh |
|
||||
Выводы:
1.двустороннее управление любой координаты объекта управления около начального уровня только при наличии избыточной или скрытой энергии, т.е. её запасов; 2.регулирование любой координаты объекта управления возможно
только в пределах ниже, максимально допустимых, т.е. управлять объектам управления по любой координате можно только при условии, что объект управления не требует большей координаты, чем та, которой обладает регулятор; 3.для быстрого управления необходима мощность. Слабомощный
регулятор быстро управлять не может; |
3 |
4.для управления надо использовать усилительные |
эффекты, т.е. |
Математические модели ОУ
у(t) – переменное состояние; |
|
x(t) – входящие сигналы; |
y t f y t , u t , t |
|
|
u(t) – выходящие сигналы. |
x t g y t , u t , t |
y1 t |
u1 t |
|
x1 t |
|
f1 |
|
g1 |
|
||||||
y2 t |
u2 t |
|
x2 t |
|
|
|
||||||||
|
. |
|
|
|
|
|
|
|
|
f2 |
g |
|
|
|
y t |
|
u t . |
|
x t . |
|
f y t ,u t ,t . |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
g y t , u t , t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
. |
|
|
. |
|
|
. |
|
|
|
||
|
|
|
u |
t |
|
|
|
|
f |
|
. |
|
||
yn t |
n |
|
|
|
xn t |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
gn |
|
|
Уравнение устройства для замера угловых скоростей |
||||||||||||||
|
выходного вала двигателя внутреннего сгорания |
|
|
|||||||||||
|
|
|
|
|
m |
d 2l |
k dl |
k |
l3 k |
|
|
|
|
|
|
|
|
|
|
dt 2 |
|
|
|
|
|||||
|
|
|
|
|
|
dt |
|
c |
|
|
|
|
|
|
|
m – масса устройства; |
|
|
|
|
|
|
|
||||||
|
l – перемещение этой массы; |
|
|
|
|
|||||||||
|
kν – коэффициент скоростного трения; |
|
|
|
||||||||||
|
kc – коэффициент жёсткости пружины; |
|
|
|
||||||||||
|
ω – угловая скорость (частота вращения). |
|
|
4 |
||||||||||
|
|
|
l |
l |
2 |
|
Введём:l l1 |
l1 |
l2 |
1 |
|
|
|
l |
k |
|
||||
|
|
|
|
l |
||
|
|
|
2 |
|
m 1 |
|
kc l3 k m 1 m
Уравнение ракеты, вертикально стартующей под действием
|
|
|
|
|
2 |
H |
|
|
силы2 |
тяги |
|
|
|
|
|
|||||
|
|
|
|
m t |
d |
|
dh |
m t g |
k |
dm t |
|
|
||||||||
|
|
|
|
dt2 |
k |
|
dt |
|
|
|
||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
k |
dm |
|
1 |
|
|
k h12 |
|
g |
|
|
|||
Получимh h1 |
|
|
|
d |
m t |
|
|
m t |
|
|
|
|||||||||
h1 |
h2 h2 |
|
|
|
|
|
||||||||||||||
|
|
Разностное уравнение для описания элементов |
||||||||||||||||||
|
|
|
|
|
|
дискретного действия |
|
|||||||||||||
|
|
|
|
|
|
|
y tk 1 f y tk |
,u tk |
,tk |
|
|
|||||||||
|
|
|
|
|
|
|
x tk g y tk ,u tk ,tk |
|
|
|||||||||||
y1 |
|
u1 |
|
|
|
x1 |
|
|
|
|
|
|
|
f1 |
|
g1 |
|
|||
|
|
u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
x2 |
|
|
|
|
|
|
|
f2 |
g2 |
||||||||
y tk . |
|
|
|
x tk |
. |
|
f y tk , u tk , tk . |
g y tk , u tk , tk . |
||||||||||||
u tk . |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
|
|
|
|
. |
|
|
|
|
|
|
|
. |
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
yn |
|
|
|
xn |
|
|
|
|
|
|
|
fn |
|
gn |
|
|||||
|
|
un |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
Такт квантования системы – это та частота, с которой опрашиваются датчики.
y k 1 T0 f y kT0 ,u kT0 , kT0 |
|
x kT0 g y kT0 , u kT0 , kT0 |
|
Для написания программы системы управления используют
три метода: |
|
U1k T0Uk |
|
|
|
|
|
|
|
|
|||
Эйлера. |
U k 1 |
|
|
|
|
|
|
|
|
||||
Адамс-Башфорт1 |
|
U1 k 1 |
2T0Uk |
|
|
|
|
|
|||||
|
U. k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
U |
k |
1 |
U |
T0 |
U |
k |
4U |
k 1 |
|
U |
k 2 |
|
|
|
||||||||||||
Адамс-Мультон.1 |
|
|
1 k 1 |
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U – сигнал (выходной, входной или сравниваемый);
To – такт квантования;
Tk-1,k-2 – предыдущие сигналы; Tk – настоящий сигнал;
Tk+1 – следующий сигнал.
6
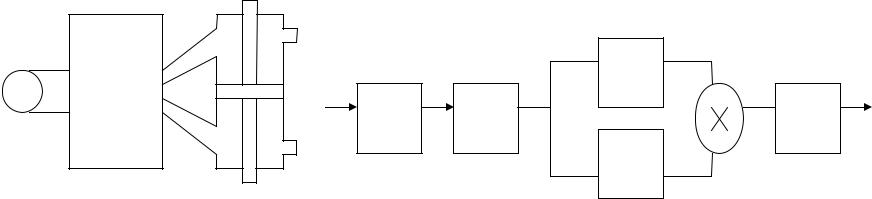
Методы линеаризации уравнений
Четыре метода линеаризации.
1.Нелинейная функция в рабочей области раскладывается в ряд Тейлора. 2.Заданные в виде графиков нелинейные функции линеаризуются в рабочей области прямыми.
3.Вместо непосредственного определения частных производных вводятся переменные в исходные уравнения.
yy0 y x x0 x u u0 u
4.Проводит линеаризации нелинейных характеристик по методу наименьших квадратов или методом трапеции.
W1 |
|
|
|
W3 |
|
W3 |
W1 |
W2 |
W4 |
|
|
|||
|
|
|
|
W3 |
W2 |
|
W4 |
|
|
7
y(t)
Сначала составить структурную схему и объединить передаточные функции. Написать, как это упростить до W1234.
При проектировании непрерывных, дискретно-непрерывных и дискретных систем необходимо знать математические модели объектов управления.
Система дискретных уравнений, передаточные функции, частотные характеристики и импульсные переходные функции удобны лишь при невысоких порядках математических моделей.
При высоких порядках моделей используют векторно-матричный аппарат записи уравнений.
Стационарный объект описывается уравнением:
y t Ay t Bu t
Ay t y t Bu t
BA y t B1 y t u t
В соответствии с этим уравнением существует типовая структурная схема многомерного объекта.
|
|
Bu(t) |
у(0) |
||||||
u(t) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
1/Р |
|
|
|
у(t) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Ау(t) |
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
8 |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
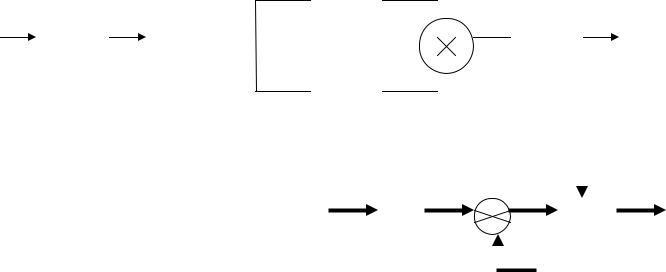
Нестационарный объект: |
y t A t y t B t u t |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W1 |
|
W2 |
|
|
|
|
|
|
|
|
|
|
W4 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
W3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A t y t y t B t u t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(t)u(t |
|
|
|
у(0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A t |
1 |
|
|
|
|
|
u(t) |
|
|
|
|
|
|
) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
В(t) |
|
|
|
|
1/Р |
|
|
|
у(t) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
y t |
|
y t u t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B t |
B t |
|
|
|
|
|
|
А(t)у(t |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А(t) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математические модели нелинейных объектов.
Весь класс существенных нелинейностей делится на 2-ве группы. К первой группе относятся однозначные нелинейности, у которых связь между входным и выходным векторными сигналами зависит только от формы статической характеристики.
9
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
y=F(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-а |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
а |
x(t)=x1(t) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-в |
y1(t)=a(x1)x1(t) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Приближённое значение передаточной функции:
y x1 a x1
Ко второй группе относятся двузначные нелинейности, у которых связь между входным и выходным сигналами зависит не только от формы статической характеристики, но и от предыстории входного сигнала.
Для учёта предыстории влияния входного сигнала, учитывается не только входной сигнал, но и скорость его изменения.
|
|
|
y |
|
в |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
-а |
0 |
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
-в |
|
|
|
|
y(t)=F[x(t)]; |
|
|
|
|
|
||||
|
|
|
|
|
|||||
x(t)=x1(t) |
|
|
|||||||
y1 t a x1 x1 |
b x1 T |
|
|||||||
2 |
x1 |
||||||||
a(x1), |
b(x1) |
– |
|
коэффициенты |
|||||
гармонической минерализации
двузначных нелинейностей; Т – период
колебаний в 1-й гармонике.
10
Эквивалентная передаточная функция: y(x1)=a(x1)+jb(x1)
~ |
~ |
~ |
x1 |
, x1 |
|
|
|
|
|
|
~ |
|
|
|
b |
|
|
|
|
|
|
|
|||||
y t F x1 , x1 |
y t a x1 , x1 |
|
|
|
|
x1 |
~ |
x1 |
~ |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 k |
|
|
y |
a |
x1 , x1 |
jb x1 , x1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
k – номер гармоники.
Матрицы и являются периодическими с периодом Т.
В случае однозначной нелинейности, матрицу коэффициентов линеаризации выбирают таким образом, чтобы минимизировать среднее значение квадрата разности между точным и приближённым сигналами на выходе.
|
|
t |
|
2 |
|
1 |
T |
|
t |
|
|
|
2 dt |
E1 t – значение по 1-й гармонике |
||
|
E |
|
lim |
|
|
|
E1 |
|
|
|||||||
|
|
|
|
|
|
|
E(t)=Y(x1)-a(x1)x1 |
|||||||||
|
|
|
|
|
T 2T |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||
В случае однозначной нелинейности
a11 |
|
|
|
x2 |
|||
a |
|
|
11 |
||||
x |
x |
||||||
|
12 |
|
|
||||
|
11 |
12 |
|||||
. |
|
|
|
|
|
||
|
|
|
. |
||||
. |
|
. |
|||||
a |
|
|
|
|
|
||
x |
x |
||||||
|
1n |
|
|
||||
|
11 |
1n |
|||||
|
. . |
|
|
|
|
1 |
|
|
|
|
|
||
x12 x11 |
x11 x11 |
|
|
||||||||||
|
|
|
F1x11 |
|
|
|
|||||||
x112 |
. . |
x1n x12 |
|
|
|
||||||||
|
|
F1x12 |
|||||||||||
. |
. . |
. |
|
|
|
|
|
|
|
||||
|
|
|
. |
|
|
|
|||||||
. |
. . |
. |
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
x12 x1n |
. . |
|
|
|
|
|
|||||||
|
x1n |
|
|
F1x1n |
|
|
|
||||||
an1
an2
.
.ann
|
|
2 |
|
||
|
|
|
x11 |
||
|
|
|
|||
|
x11 x12 |
||||
|
|
|
|
||
|
|
|
|||
|
. |
||||
|
. |
||||
|
|
|
|
|
|
|
|
|
|||
|
x11 x1n |
||||
x12 x11 x122
.
.
x12 x1n
. . |
|
|
|
|
|
1 |
|
|
|
|
|
|
x x |
|
F x |
||||||||
. . |
|
1n 11 |
|
|
1 11 |
|
|
||||
|
x1n x12 |
|
|
|
F1 x12 |
|
|||||
. . |
|
. |
|
|
|
|
|
|
|||
|
|
|
|
. |
|
|
|||||
. . |
|
. |
|
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
. . |
|
2 |
|
|
|||||||
|
|
|
|
|
|||||||
|
|
x1n |
|
|
F1 x1n |
|
|
||||
11