5 Построение логарифмической амплитудо-частотной характеристики и логарифмической фазо-частотной характеристики системы

Передаточная функция системы после z-преобразования

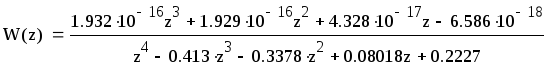^{. (51)}

Для перехода к псевдочастоте осуществим биполярные преобразования, используя программу Mathcad. Для этого произведем подстановку

^{, (52)}

^{. (53)}

Перейдем от ω-изображению к передаточной функции от псевдочастоты, сделав подстановку

^{, (54)}

^{. (55)}

Таким образом, мы получили функцию ω-изображения

⁽⁵⁶⁾

ЛАЧХ и ЛФЧХ, построенные в программе Mathlab, представлено на ри-сунке 6.

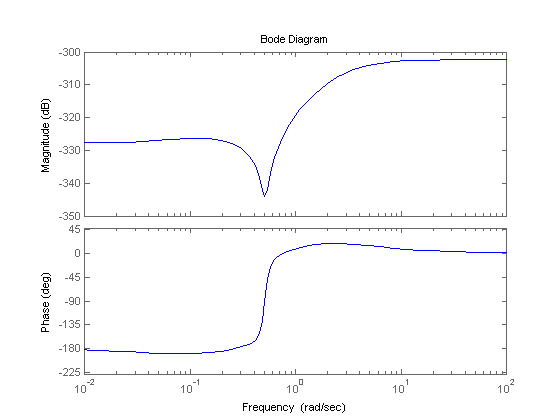
Рисунок 6 — ЛАЧХ и ЛФЧХ системы

Вывод. В данном разделе курсовой работы был произведен переход передаточной функции к псевдочастоте и построение ЛАЧХ и ЛФЧХ системы. Из полученных графиков следует, что система имеет отрицательный коэффициент усиления и не имеет запаса устойчивости по фазе, следовательно необходимо провести коррекцию системы.

6 Постороение желаемой логарифмической амплитудо-частотной характеристики системы, логарифмической амплитудо-частотной характеристики корректирующего устройства

Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства. Строится желаемая ЛАЧХ на основании требований к системе. Низкочастотная асимптота ЛАЧХ разомкнутой системы определяет статические свойства. Если передаточная функция разомкнутой системы имеет передаточный коэффициент и порядок астатизма , удовлетворяющий требованиям, то низкочастотная асимптота желаемой ЛАЧХ является низкочастотной асимптотой неизменной части системы.

Среднечастотная асимптота ЛАЧХ разомкнутой системы и её сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики. Построение среднечастотной асимптоты желаемой ЛАЧХ начинают с выбора частоты среза . Для этого используют номограммы В.В. Солодовникова. Она определяет зависимость перерегулирования и времени регулирования от максимума вещественной частотной характеристики замкнутой системы, причем время регулирования дано в виде в виде функции частоты среза . По заданному значению перерегулирования определяют значение . Затем по определяют соотношения между и .

Высокочастотная асимптота желаемой ЛАЧХ мало влияет на свойства системы. Поэтому ее выбирают так, чтобы корректирующее устройство было возможно более простое. Это достигается при совмещении высокочастотных асимптот характеристик и . Если совмещение не удается, то высокочастотная асимптота должна иметь тот же наклон, что и высокочастотная асимптота .

Так как система является дискретной, то необходимо определить запретную зону, для этого найдем рабочую точку

А , (57)

где — скорость изменения входного сигнала;

— ускорение изменения входного сигнала;

— точность прохождения сигнала.

Зададим значения

об/сек;

об/сек²;

– допустимая ошибка

Значение частоты рабочей точки

с^-1. (58)

Значение амплитуды рабочей точки

. дБ (59)

Таким образом, рабочая точка

.

Через полученную точку проводим прямую с наклоном -20 дБ/дек. Эта прямая является верхней границей запретной зоны.

По номограмме Солодовникова и заданному в техническом задании желаемому перерегулированию % и времени регулирования c определяем частоту среза

, (60)

с^-1.

Рисунок 7 — Реальная, аппроксимированная, желаемая ЛАЧХ и ЛАЧХ корректирующего устройства

Перейдем к псевдочастоте

, (61)

, (62)

.

Наклон ЖЛАЧХ в среднечастотной области должен быть -20 дБ/дек, через частоту среза в этой области проводим прямую с наклоном -20 дБ/дек. В высоко-частотной области ЖЛАЧХ сопрягается с исходной ЛАЧХ, то есть будет иметь такие же наклоны. Низкочастотная область не имеет большого значения, поэтому достраивается произвольно.

Для улучшения параметров системы в ней необходимо установить последовательно-параллельное корректирующее устройство.

По таблицам из атласа Топчеева, подберем, корректирующее устройство, представленное на рисунке 8, с передаточной функцией:

, (63)

, (64)

. (65)

Рисунок 8 — Электрическая схема корректирующего устройства

Зададим значения

Ом,

Ом,

Ф,

,

.

Передаточная функция корректирующего устройства

. (66)

Произведем обратное преобразование Лапласа с помощью программы Mathcad и получим передаточную функцию корректирующего устройства в z-форме

. (67)

Проведем анализ скорректированной системы.

Передаточная функция ЖЛАЧХ

. (68)

Построим переходный процесс для скорректированной системы и оценим показатели качества системы. Переходный процесс представлен на рисунке 9.

Рисунок 9 — Переходный процесс скорректированной системы

По графику переходного процесса, представленному определим прямые оценки качества системы:

- установившееся значение h_уст=;

- максимальное значение h_max=;

- время первого согласования t₁=0,4 с;

- время нарастания переходного процесса t_н=0,6 с;

- время регулирования t_р=1,5;

- перерегулирование 19%.

Вывод. Для улучшения параметров системы было рассчитано последо-вательно-параллельное корректирующее устройство. При включении корректирующего устройства в систему, были получены требуемые характеристики.