К расчету плоских статически определимых комбинированных систем. Комбинированные системы.

Комбинированные системы – это неизменяемые системы, составленные из двух или нескольких систем (простых и шарнирных балок, арок, балочных и арочных ферм, рам, шарнирных стержневых и дисковых цепей и т.д.), соединенных между собой дополнительными связями для совместной работы.

Мы ограничимся рассмотрением комбинированных систем, состоящих из балок и балочных ферм, соединенных с шарнирной цепью, как наиболее часто встречающихся.

Они бывают: висячие (рис 1) и арочные (рис 2).

Висячие комбинированные системы – те, в которых балка или ферма усилена шарнирной цепью, работающей на растяжение при вертикальной нагрузке, направленной вниз.

Арочные комбинированные системы – те, в которых балка или ферма усилена цепью, работающей на сжатие.

Балки и фермы, усиленные цепью, могут быть однопролетными и многопролетными, статически неопределимыми.

Комбинированные системы применяются прежде всего в мостах, поэтому их чаще всего рассчитывают на подвижную нагрузку.

Линии влияния опорных реакций в висячих комбинированных системах.

Разрежем цепь над опорами балки или фермы, отбросим ее крайние части, и продольные силы в разрезанном стержне цепи разложим на вертикальные и горизонтальные составляющие. Система симметрична и эти точки находятся на одном уровне.

Составим уравнения равновесия:

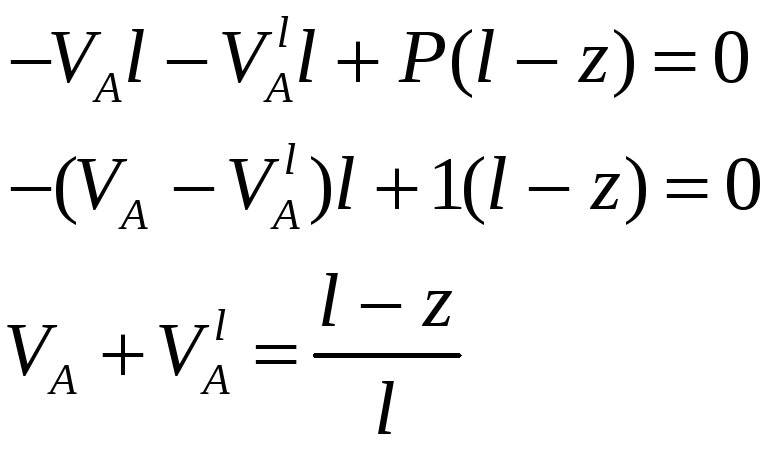(1)

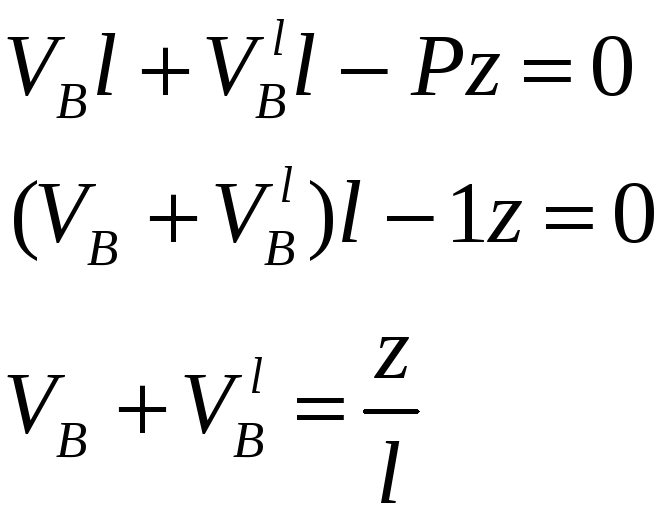(2)

Значит сумма сил V и V^l равна опорным реакциям простой балки, л.в. которых известны.

Вырежем любой «n»-ый узел цепи и рассмотрим его равновесие:

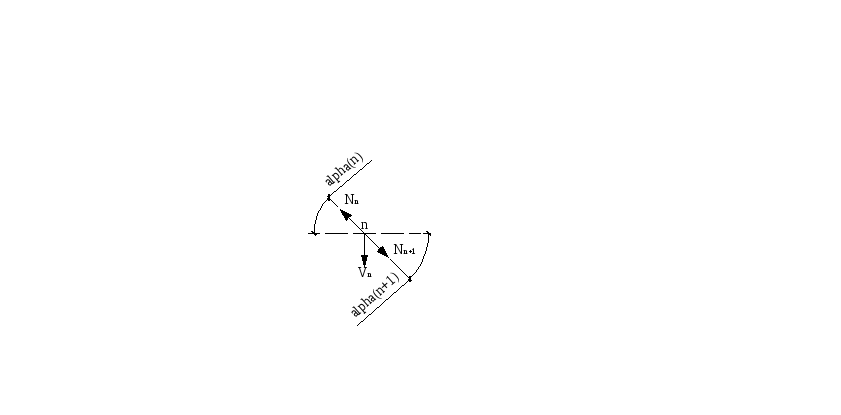
Примем эту величину за распор цепи Н, т.е.

(3) - продольная сила в элементах цепи.

(4) - продольная сила в подвесках.

Вертикальные составляющие продольных сил в крайних элементах цепи:

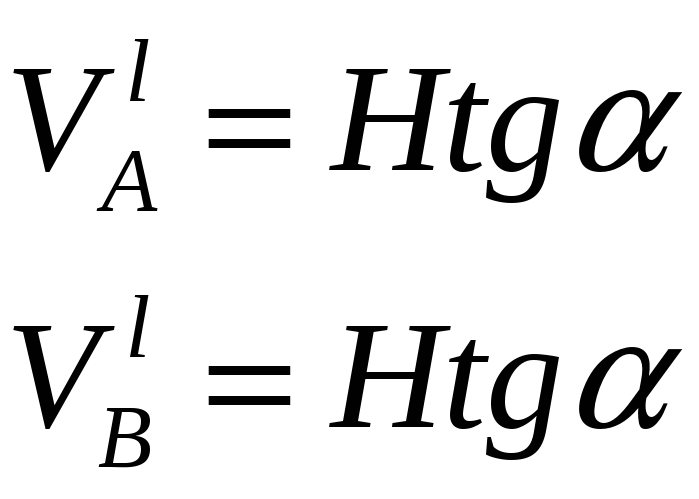
Тогда с учетом (1) и (2) получим опорные реакции балок:

(5) л.в. прост. балки – л.в. /

Как видно, л.в. опорных реакций и внутренних сил цепи, подвесок определяются л.в. распора цепи Н. Для ее построения дополнительно разрежем средний стержень цепи над шарниром балки С и найдем:

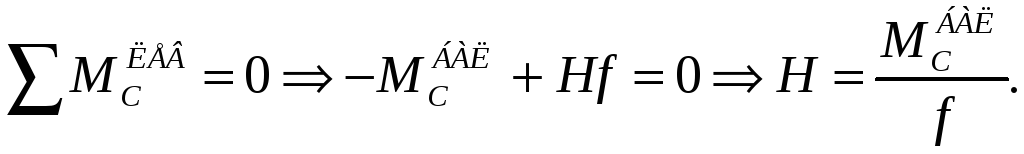(6)

где - момент всех левых вертикальных сил относительно С, равный моменту в простой балке, относительно такой же точки.

Значит л.в. распора получается как л.в. распора висячей вспомогательной трехшарнирной системы, проходящей по цепи и шарнирам А^lC^lB^l. (рис 1)

Л.в. реакций балки строится по (5) (рис 2).

Линии влияния внутренних сил в висячих комбинированных системах.

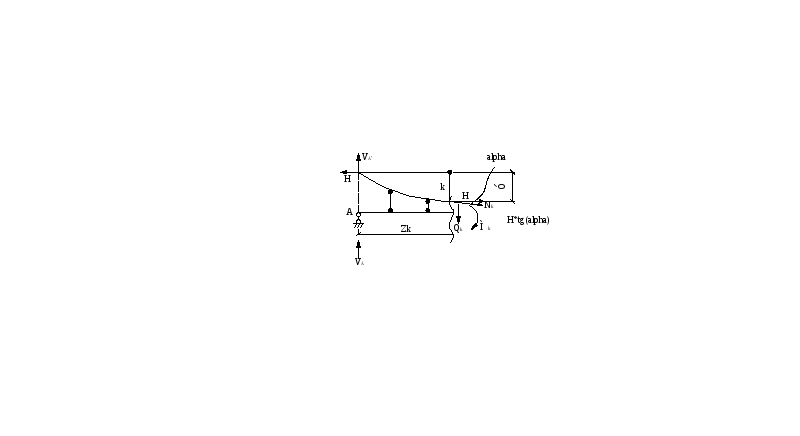
Разрежем цепь в сечении «к», продольную силу в цепи N_К разложим на Н и .

В балке возникает Q_K и М_К. Тогда

- поперечная сила и изгибающий момент в простой балке.

Значит, л.в. внутренних усилий получаются по л.в. балок с вычетом . (рис 3)

Линии влияния опорных реакций и внутренних сил в арочных комбинированных системах.

Разрежем крайние стержни цепи в точках над опорами балки или фермы и разложим продольную силу в стержне цепи на вертикальные и горизонтальные составляющие, по аналогии с рассмотренными выше заданиями. Тогда расчет балки аналогичен, т.е. все полученные формулы сохраняются, только стержни арки и стойки будут сжаты.

Построим л.в. М_К и Q_К по нулевым точкам. Для М_К нулевая точка будет в пересечении () ( - точка на арке под сечением балки) и ().

Для Q_К н.т. – в пересечении прямой, проведенной из точки , параллельной разрезанному элементу шарнирной арки и ().