2.1.1 Технические характеристики двигателя :

Типоразмер ПН-5

Номинальная мощность Рн, КВт 1

Номинальное количество оборотов n_н, об/мин 2800

Номинальный ток I, А 0,585

Коэффициент полезного действия ,% 88,6

Номинальное напряжение Uн, В 120

Момент инерции ротора J, кгмм^-4 0,03

Вид исполнения (закрытое исполнение) IP 54

2.1.2 Расчет передаточной функции. Двигатель постоянного тока имеет передаточную функцию вида:

Wдв(P) = ,

где k_дв – коэффициент усиления;

T_дв – электромеханическая постоянная электродвигателя.

Передаточная функция исполнительного двигателя:

Вычислим передаточную функцию, определив коэффициенты: k_дв, Т_м.

Постоянная времени по моменту:

где С_е – электрическая постоянная, зависящая от конструкции двигателя.

С_е вычислим следующим образом.

Уравнение якорной цепи:

В установившемся (номинальном) режиме I_я = const, поэтому

Так как , то:

Решим уравнение относительно С_е.

Учитывая паспортные данные, определенные при выборе двигателя, вычислим С_е.

С учетом найденных коэффициентов запишем передаточную функцию исполнительного двигателя:

Передаточная функция запишется в следующем виде:

Wдв(P) = .

2.2 Расчет зубчатой конической передачи

Выбираем редуктор с конической зубчатой передачей, так как именно этот вид передачи наиболее подходит для больших передаточных чисел.

Выбор материала и определение допускаемых напряжений.

Для шестерни: сталь 45, улучшение, тв. 295 НВ, [σ_H]₁=432 МПа, [σ_F]₁=240 МПа.

Для колеса: сталь 45, нормализация, тв. 210 НВ, [σ_H]₂=400 МПа, [σ_F]₂=175 МПа

([σ_H] - допускаемое контактное напряжение, [σ_F] - допускаемое напряжение при изгибе).

Общее контактное напряжение для прямозубой (зубчатой конической) передачи:

[σ_H]= [σ_H]_min=400 МПа.

Внешний делительный диаметр колеса определяется по следующей формуле:

,

где T_K - крутящий момент ведомого колеса рассчитываемой передачи,

T_K=31·10³ Н·мм;

U==280 – передаточное отношение рассчитываемой передачи;

=0,3 -коэффициент длины зуба;

[σ_H]=400 МПа - общее контактное напряжение передачи;

-коэффициент, учитывающий распределение нагрузки по длине зуба, выбирается в зависимости от ψ_bd, ,- коэффициент ширины колеса, выбирается из значений (0.2; 0.4; 0.5; 0.8).

Определим :

Примем=0,2, тогда

;

=1,25,[1,т.9.11].

(мм).

Определение число зубьев шестерни и колеса.

Назначим число зубьев шестерни Z₁=21, тогда число зубьев ведомого колеса: Z₂=Z₁·U=21·4.3≈91.

Внешний окружной модуль:

(мм).

Округляя по ГОСТ, получим мм

Уточним внешний делительный диаметр

(мм).

Округляя по ГОСТ, получим (мм)

Конусное расстояние определяется по формуле:

(мм).

Длина зуба или ширина зубчатого венца определяется по формуле:

(мм).

Округляя по ГОСТ, получим b=127 мм

Определим углы при вершинах начальных конусов:

для шестерни: , откуда,

для колеса

Средний делительный диаметр шестерни:

(мм).

Средний окружной модуль

(мм).

По ГОСТ принимаем модуль мм.

Средняя окружная скорость передачи ,

где n_ш - число оборотов вала, на который насажена шестерня, об/мин;

.

Назначим степень точности передачи: S=9

Средний делительный диаметр колеса определим графически.

Определим внешний делительный диаметр шестерни:

(мм).

Примем =190 мм.

М1:5

Рисунок 2 - Средний делительный диаметр колеса

мм;

мм;

b=127 мм.

Графически определяем, что d₂≈770 (мм).

Проверочный расчет передачи на контактную прочность:

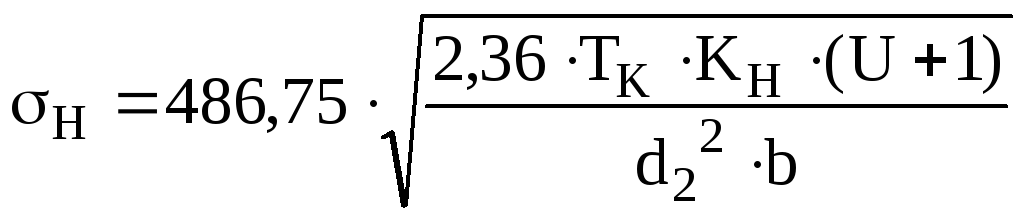≤[σ_H],

где [σ_H]=400 МПа,

K_H-коэффициент нагрузки, K_H=K_Hα ·K_Hβ·K_Hυ, где

K_Hα – коэффициент распределения нагрузки между зубьями, K_Hα=1 (для прямозубой передачи),

K_Hβ – коэффициент, учитывающий распределение нагрузки по длине зуба,

K_Hβ =1,25 ;

K_Hυ – коэффициент динамичности нагрузки, K_Hυ =1,

т.е. K_H=K_Hα ·K_Hβ·K_Hυ=1·1,25·1=1,25.

<400МПа.

Условие прочности выполняется.

Рассчитаем основные размеры шестерни и колеса.

Параметры шестерни:

(мм);

(мм),

где - диаметр выступов зубьев шестерни, мм;

- диаметр впадин зубьев шестерни, мм;

Параметры колеса:

(мм);

(мм).

-диаметр выступов зубьев ведомого колеса, мм;

-диаметр впадин зубьев ведомого колеса, мм.