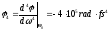1.2. Спектрально ограниченный оптический импульс в среде с дисперсией [1]

Уравнения Максвелла для линейной изотропной среды:

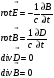(1.39)

Распространение волнового пакета с напряженностью поля E(t,z) в изотропной дисперсионной среде описывается скалярным волновым уравнением

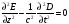(1.40)

и материальным уравнением

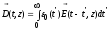. (1.41)

Фурье представление для поля E(t,z) при 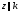имеют вид

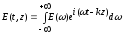(1.42)

Из (40-42) следует дисперсионное соотношение для k()

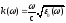(1.43)

где ₀ - диэлектрическая проницаемость среды, определяемая выражением

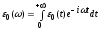. (1.44)

Если известен вид функции (), то уравнения (40) позволяет определить поле в любой точке дисперсионной среды..

Метод медленно меняющихся амплитуд

Пусть ₀ - средняя частота спектрального пакета. Если амплитуда поля импульса медленно меняется на периоде колебания T₀=2/₀, то есть выполняется условие, что длительность импульса ₀ T₀, то решение (1.40-41) можно искать в виде

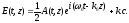(1.45)

где 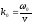, а 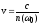- фазовая скорость.

Учитывая, что изменения комплексной амплитуды на периоде поля малы, разложим ее в ряд Тейлора по t'

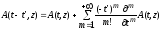, (1.46)

учитывая, что

(1.47)

получим

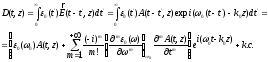(1.48)

Тогда волновое уравнение для амплитуды поля A(t,z) можно представить в виде:

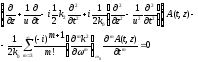, (1.49)

где введено понятие групповой скорости u

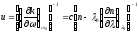(1.50)

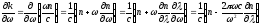
так как 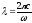и .

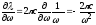Дисперсия групповой скорости k₂

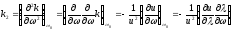
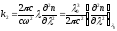(1.51)

Дисперсия групповой скорости k₃ во втором приближении

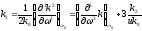(1.52)

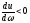-- нормальная дисперсия , 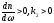, (1.53)

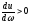-- аномальная дисперсия, 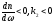. (1.54)

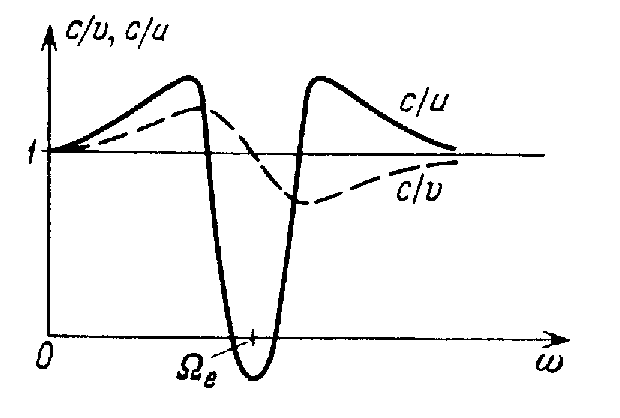
Рис.1.7. Частотная зависимость групповой и фазовой скорости вблизи резонанса _е.

Пример: плазма - ,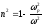

групповая скорость - ,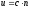

фазовая скорость - ,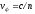

соотношение между групповой и фазовой скоростями:

u·v_ф=с².

Приближения теории дисперсии

Аппроксимация дисперсионных свойств среды представлением k() в виде разложения:

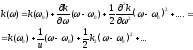(1.55)

Нулевое приближение

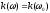
Решение волнового уравнения (1.49) дает

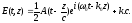(1.56)

Первое приближение

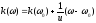(1.57)

Волновое уравнение (1.49) в первом приближении теории дисперсии имеет вид

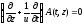(1.58)

С учетом решения уравнения (1.58) для напряженности поля будем иметь

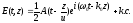(1.59)

Второе приближение

Волновое уравнение (1.49) для амплитуды поля А(t,z) во втором приближении теории дисперсии имеет вид:

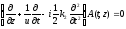(1.60)

(эллиптическое уравнение ).

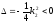Перейдем к бегущей системе координат

,

, ,

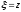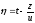
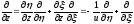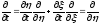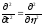
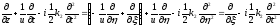
Получим уравнение:

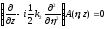, (1.61)

решение которого выражается через функцию Грина (интеграл Дюамеля)

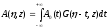, (1.62)

где G-функция Грина.

Функция Грина должна удовлетворять уравнению:

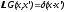, (1.63)

где 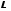- дифференциальный оператор .

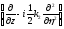Введем новую функцию

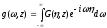. (1.64)

Применим Фурье преобразование к (1.63) с учетом (1.64) имеем

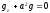, (1.65)

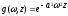, (1.66)

где .

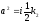Применяя обратное преобразование Фурье к (1.66), которое сводится к взятию интеграла пуассоновского вида:

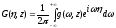, (1.67)

получим

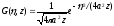. (1.68)

Откуда

(1.69)

Решение уравнения (1.61) в виде (1.62-69) удовлетворяет граничной задаче

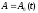при z=0.

При этом амплитуда поля в общем случае комплексна

,

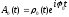где 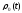действительная огибающая.

Решение волнового уравнения для спектрально ограниченного импульса с огибающей гауссова вида

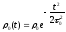. (1.70)

Согласно (1.62) {,}

,

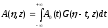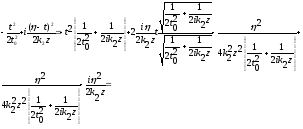
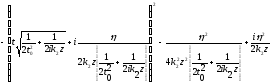, (1.71)

Решение будет иметь вид

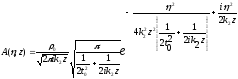(1.72)

после преобразования

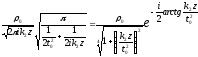
имеем

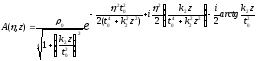. (1.73)

Введем

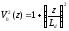, (1.74)

где - дисперсионная длина или длина дисперсионного расплывания,

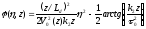- (1.75)

Тогда комплексную амплитуду можно представить в виде:

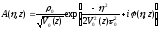. (1.76)

В соответствии с (1.76) гауссов импульс сохраняет вид огибающей, но приобретает линейную частотную модуляцию, знак которой определяется знаком k_2.

Из (1.76) следует, что длительность гауссова импульса растет с расстоянием по закону

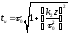(по уровню e^-1). (1.77)

Согласно (1.77)

при z<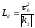 длительность импульса практически не меняется , ,

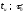при z>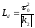длительность растет линейно по z,

. (1.78)

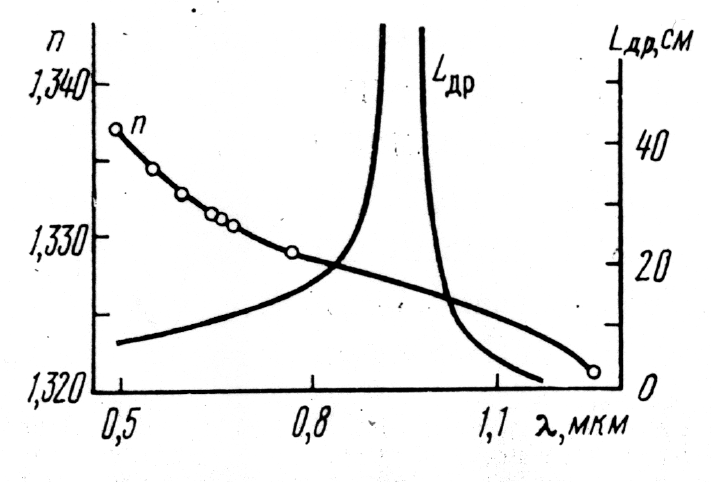
Рис.1.8. Дисперсия показателя преломления и длины расплывания гауссова импульса в воде.

Дисперсионное расплывание импульса увеличивается с приближением его формы к прямоугольной.

Для более коротких импульсов дисперсионное расплывание более сильное.

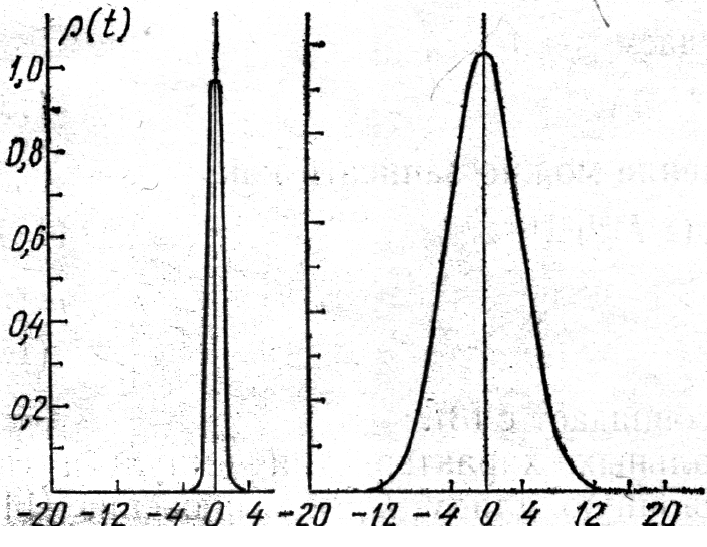/₀

1. (b)

Рис. 1.9. Огибающая спектрально ограниченного импульса в среде с квадратичной дисперсией при z/L_d<1 (a) и z/L_d>1 (b).

/₀ - относительная длительность импульса

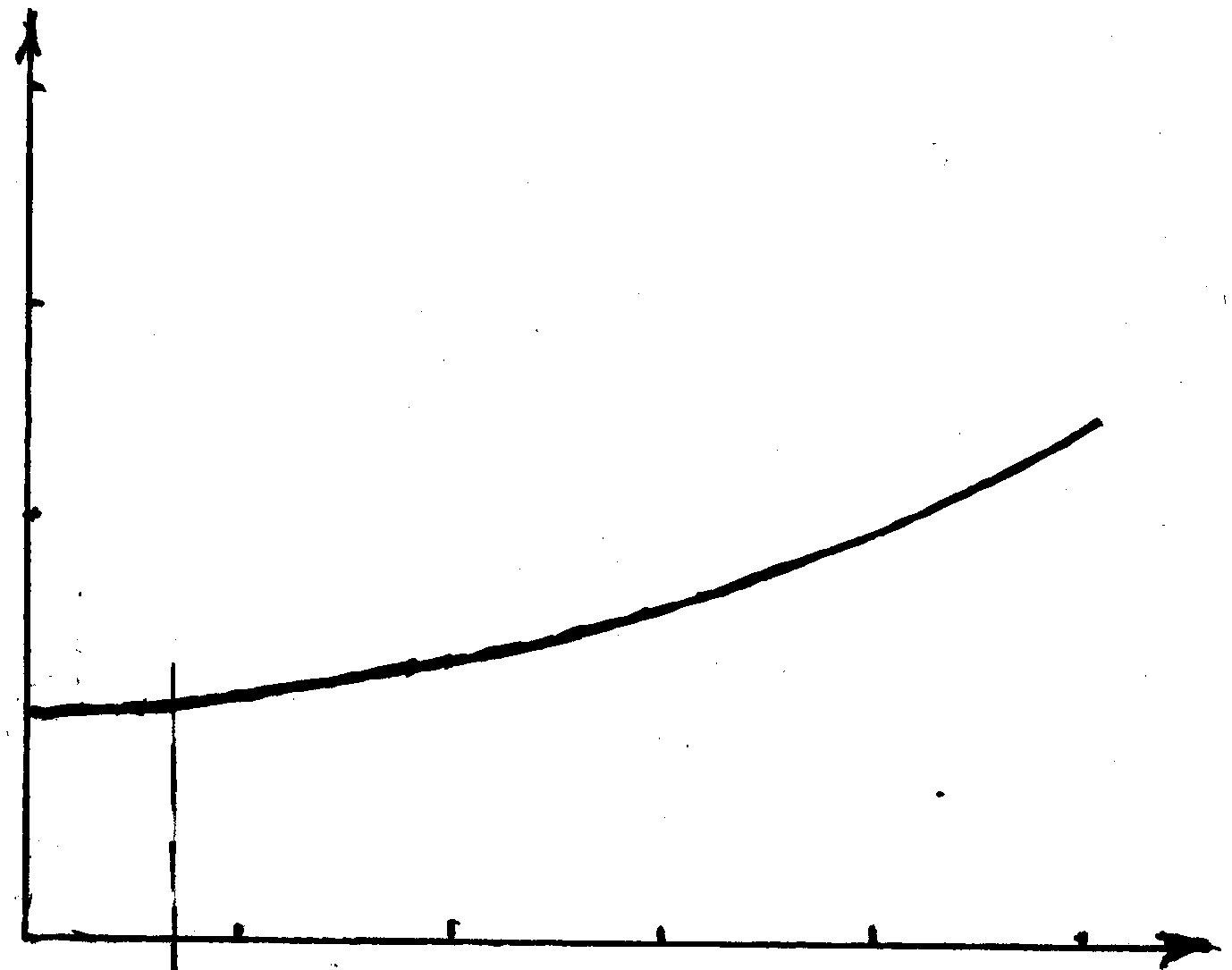
1 2 3 4 z/L_d

Рис. 1.10. Зависимость длительности импульса в среде c квадратичной дисперсией от расстояния.

Среда с квадратичной дисперсией:

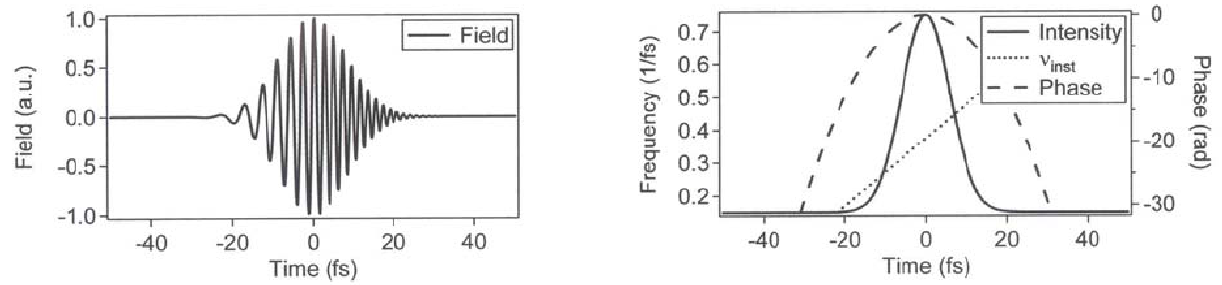
Рис. 1.11. Гауссов импульс в среде с нормальной дисперсией: k₂>0,. .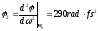

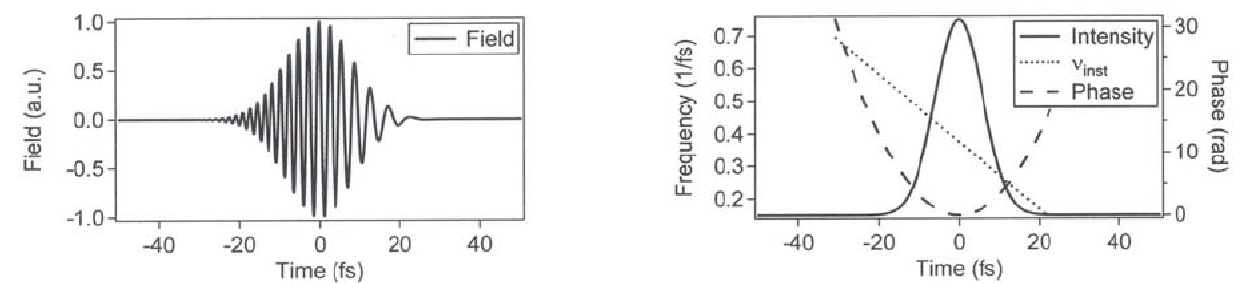
Рис. 1.12. Гауссов импульс в среде с аномальной дисперсией: k₂<0, .

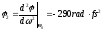РЕЗЮМЕ:

Спектрально ограниченный гауссов импульс в среде с квадратичной дисперсией:

• сохраняет свою форму,

• расплывается,

• приобретает линейную частотную модуляцию,

• т.е. перестает быть спектрально ограниченным.

Третье приближение теории дисперсии

Уравнение для амплитуды поля А(t,z) в третьем приближении теории дисперсии имеет вид:

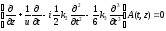(1.79)

В бегущей системе координат

,

,,

,

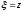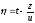
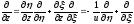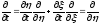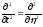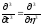
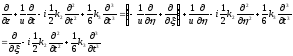
Получаем следующие уравнение:

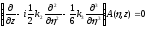, (1.80)

решение выражается через интеграл

, (1.81)

где G-функция Грина,

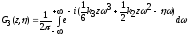. (1.87)

Амплитуда A(t,z) для гауссова импульса может быть найдена только в пределе t , вид огибающей (t,z) определяется обычно численным методом.

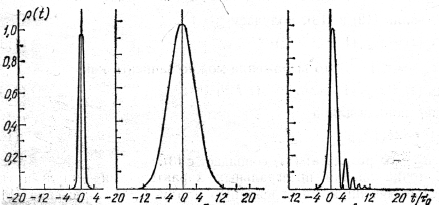
k₂=0 и k₃=0 k₂0 и k₃=0 k₂=0 и k₃0

Рис. 1.13. Огибающая спектрально ограниченного импульса в средах с k₂0 и k₃0.

Кубическая дисперсия при k₃>0 приводит к модуляции хвоста импульса, передний фронт остается гладким. Импульс становится асимметричным, его максимум смещается. С уменьшением ₀ роль k₃ возрастает. Условием малости квадратичной дисперсии в сравнении с кубической есть

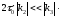. (1.88)

Характерная длина дисперсионного расплывания при этом определяется соотношением

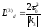. (1.89)

При z>>L⁽³⁾_d длительность импульса в среде при k₂=0 определяется выражением

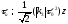. (1.90)

Среда с кубической дисперсией:

1. положительная кубическая спектральная фаза

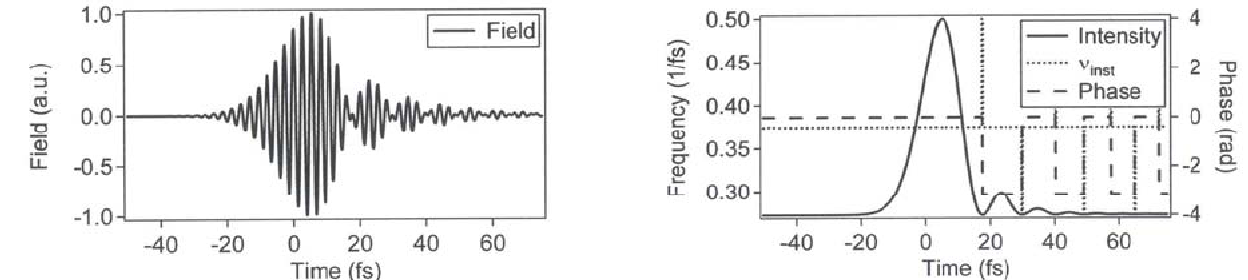
Рис. 1.14. Гауссов импульс в среде с k₂=0, k₃>0: .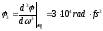

2. отрицательная кубическая спектральная фаза:

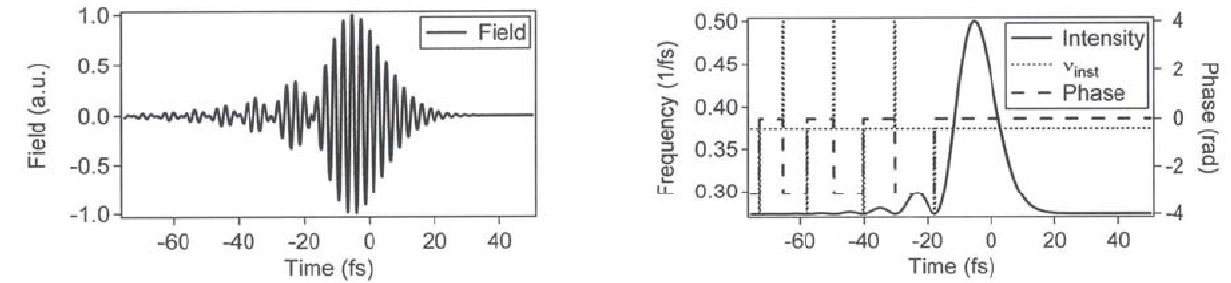
Рис. 1.14. Гауссов импульс в среде с k₂=0, k₃<0: .

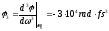Среда с дисперсией четвертого порядка:

1. положительная спектральная фаза четвертого порядка

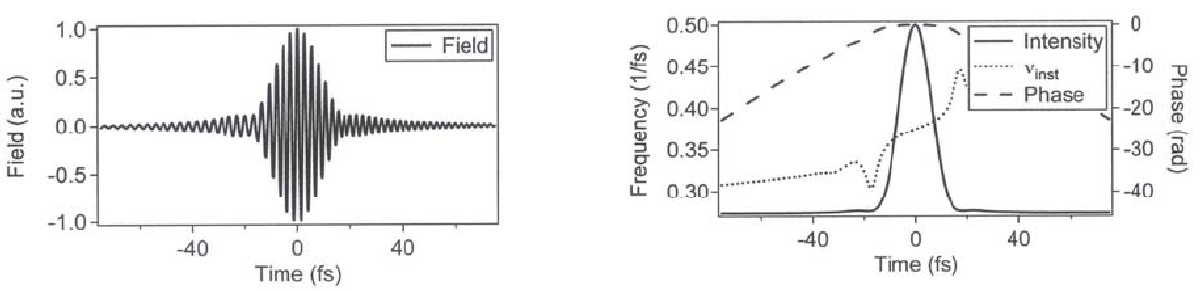
Рис. 1.15. Гауссов импульс в среде с k₂=0, k₃=0, k₄>0:

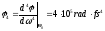
2. отрицательная спектральная фаза четвертого порядка:

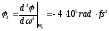
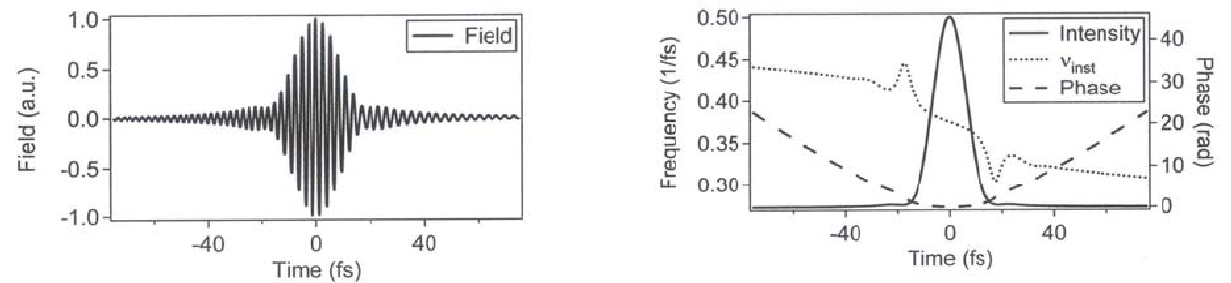
Рис. 1.16. Гауссов импульс в среде с k₂=0, k₃=0, k₄<0: