Правила округлення:

1. Якщо перша з відкинутих цифр менше 5, то десяткові знаки, які залишилися, зберігаються без змін.

2. Якщо перша з відкинутих цифр більше 5 або дорівнює 5 і серед інших відкинутих цифр є ненульові, то до останньої цифри, що залишилася, додається одиниця.

3. Якщо перша з відкинутих цифр дорівнює 5 і інші відкинуті цифри є нульовими, то остання цифри, що залишилася, не змінюється, якщо вона парна, і збільшується на одиницю, якщо вона непарна.

Приклад 3. Округлити число до семи, шести, п’яти і т.д. десяткових знаків і до одиниць.

Розв’язання. За правилом округлення:

(за правилом 3);

(за правилом 2);

(за правилом 2);

(за правилом 1);

(за правилом 2);

(за правилом 2);

(за правилом 1);

(за правилом 2).

Абсолютна і відносна похибки записуються у вигляді чисел з одною або двома значущими цифрами, і вони округлюються з надлишком. В записі наближених чисел вони вказуються так:

;

Так, для числа з прикладу 1б)

; .

Приклад 4. Виділити вірні значущі цифри наступних чисел:

1) ; ;

2) ; ;

3) ; .

Розв’язання. Виділимо вірні значущі цифри підкреслюванням.

1) , оскільки ;

2) , оскільки ;

3) , оскільки .

Похибки округлення в ЕОМ числа , які обумовлені скінченністю розрядної сітки, для різних комп’ютерів можуть бути обчислені за формулою:

,

де – перша значуща (відмінна від нуля) цифра; – основа системи числення, що використовується в комп’ютері; – розрядність комп’ютера ( для стандартної точності і для подвійної точності – для ЕОМ типу IBM).

Приклад. Користуючись розкладом , обчислити величину з вірними цифрами після коми. ( – номер варіанта)

Тема 2. Похибки обчислень

7. Дії над наближеними числами Похибки обчислень

Нехай , і задані абсолютні і відносні похибки їх наближень, тобто: , ; , .

Сформулюємо правила обчислення похибок при виконуванні операцій над наближеними числами.

1. При додаванні або відніманні двох наближених чисел їх абсолютні похибки додаються:

.

2. При множенні або діленні двох наближених чисел їх відносні похибки додаються:

;

.

3. При піднесенні до степеня наближеного числа його відносна похибка множиться на показник степеня:

4. Відносна похибка суми додатних доданків міститься між найбільшим і найменшим значеннями відносних похибок цих доданків:

,

де , .

На практиці для оцінки похибки приймають найбільше значення .

Зауваження. Операції додавання, множення та ін. наближених чисел не є звичайними арифметичними операціями, вони наближено зображають звичайні арифметичні операції. Крім того, наближені арифметичні операції мають зовсім інші властивості, ніж точні. Наприклад, вони не є асоціативними, не виконується закон дистрибутивності, добуток ненульових множників може виявитися рівним нулю („виникнення машинного нуля при множенні”).

Приклад. Обчислити і визначити похибки результату, використовуючи правила обчислення похибок для арифметичних операцій:

,

де , , .

Розв’язання. Обчислимо:

.

Визначимо відносні похибки даних:

;

;

.

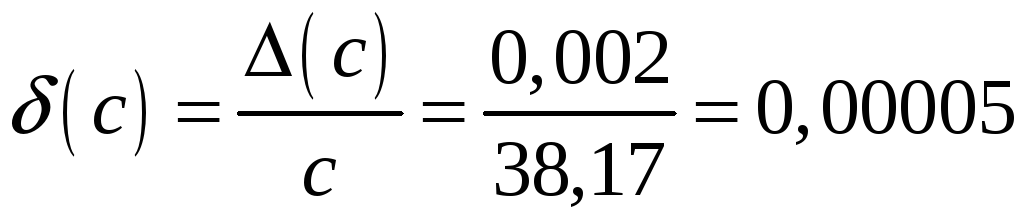Тоді за правилами 2, 3 обчислення похибок при виконанні арифметичних операцій будемо мати:

.

Визначимо відносні похибки і . За правилом 1

;

.

Тоді

;

.

Отже,

;

.

Таким чином,

;

.