4. Поняття похибки наближення Абсолютна та відносна похибки

Нехай – точне, але, як правило, невідоме значення деякої величини, а – її відоме наближене значення (наближення). У цьому випадку пишуть .

Означення. Абсолютною похибкою деякого числа називається абсолютна величина різниці між його істинним значенням і наближеним значенням, отриманим в результаті обчислення або вимірювання. Позначається .

.

Означення. Відносною похибкою деякого числа називається відношення його абсолютної похибки до модуля наближеного значення . Позначається .

.

Зауваження. В загальному випадку має розмірність величини , а – безрозмірна величина. Часто обчислюється в процентах, тоді вона множиться на 100%.

Оскільки істинне значення величини звичайно невідоме, то наведені вирази для похибок практично не можуть бути використані. Є лише наближене значення і для нього вводиться поняття граничної похибки.

Означення. Граничною абсолютною похибкою наближення називається число , яке не менше абсолютної похибки, тобто

(1)

Розкриваючи в останній нерівності модуль, отримаємо відрізок, який містить точне значення :

.

Граничною відносною похибкою наближення називається відношення граничної абсолютної похибки до модуля числа :

(2)

Звідси випливає наступне співвідношення, яке часто застосовується на практиці:

.

Далі розглядатимемо тільки граничні абсолютну і відносну похибки, для скорочення опускаючи слово "гранична". Також для спрощення запису покладемо

; .

Приклад 1. Знайти абсолютну і відносну похибки числа , заданого а) двома; б) трьома цифрами після коми.

Розв’язання. а) Нехай . Тоді за формулою (1)

: ;

за формулою (2):

: .

б) Нехай . Тоді за формулою (1)

: ;

за формулою (2):

: .

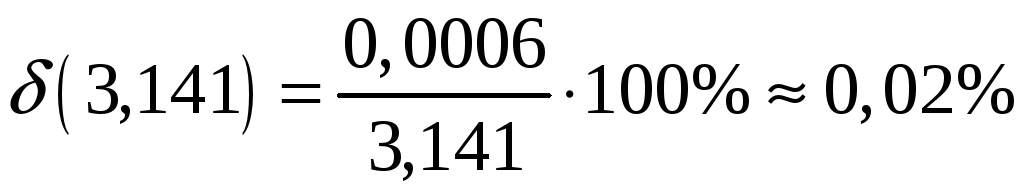5. Машинний епсілон

Оцінимо величину похибки подання дійсного числа в машинній системі числення. Два найближчих машинних числа можуть бути представлені у вигляді:

;

.

Абсолютна «відстань» між ними дорівнює:

,

а відносна «відстань» визначається виразом:

Звідси ясно, що похибка подання будь-якого дійсного числа , такого, що , задовольняє нерівності:

(3)

де – машинне подання дійсного числа .

Права частина нерівності (3) називається машинним епсилоном і позначається . Машинний епсилон – найважливіший параметр обчислювальної системи. Він характеризує відносну помилку подання дійсних чисел в пам'яті комп'ютера у формі з плаваючою комою. Отримані вирази дають підставу стверджувати, що будь-яке число в інтервалі у машинному поданні не буде відрізнятися від 1. Звідси випливає простий алгоритм обчислення машинного епсилона:

Крок 1. ;

Крок 2. Якщо , то ;

Крок 3. .

6. Число вірних значущих цифр наближеного числа. Правила округлення

Наведені оцінки похибок наближених чисел справедливі, якщо в записі цих чисел всі значущі цифри вірні. Нагадаємо означення цих понять.

Запишемо додатне число у вигляді скінченного десяткового дробу:

,

або

,

де всі коефіцієнти і менші за число 10.

Означення. Значущими цифрами наближеного числа називаються всі цифри в його записі, починаючи з першої ненульової зліва.

Приклад 2. Виділити значущі цифри наступних чисел:

1) 0,037; 2) 14,80; 3) 0,00167; 4) 3250000; 5) 0,00005.

Розв’язання. Виділимо значущі цифри підкреслюванням. За означенням:

1) 0,037; 2) 14,80; 3) 0,00167; 4) 3250000; 5) 0,00005.

Означення. Перші значущих цифр наближеного числа називаються вірними, якщо абсолютна похибка цього числа не перебільшує половини одиниці розряду, який відповідає -й значущій цифрі, тобто

.

Зайві збережені цифри, крім вірних, називаються сумнівними.

Обчислити наближене число з точністю означає, що необхідно зберегти вірною значущу цифру, яка стоїть в -му розряді після коми.

На практиці при виконанні обчислень часто виникає потреба в округленні наближеного числа.

Означення. Округленням наближеного числа називається заміна його числом з меншою кількістю значущих цифр.

Для округлення числа до значущих цифр треба відкинути всі його цифри, які стоять справа від -ї значущої цифри. При цьому користуються наступними правилами: