2.12 Серийный тест
2.12.1 Назначение теста
В этом тесте рассматривается частота всех возможных перекрывающихся m-битных комбинаций по длине всей последовательности. Цель этого теста - определить равно ли примерно количество появлений 2m m-битных комбинаций значению для случайной последовательности. Случайные последовательности обладают равномерностью, т.е. каждая m-битная комбинация имеет такую же вероятность появления, как и любая другая m-битная комбинация. Отметим, что для m=1 серийный тест эквивалентен частотному тесту (см п. 2.1).
2.12.2 Вызов функций
Serial(m,n), где:
m - длина каждого блока в битах,
n - длина битовой строки в битах.
Дополнительные входные параметры, используемые функцией, но определяемые тестирующим кодом:
-
битовая последовательность, генерируемая
тестируемым ГСЧ или ГПСЧ; это глобальная
структура, которая должна быть определена
в момент вызова функции;
=
1,
2,…,
n.
2.12.3 Статистика теста и контрольное распределение
-
количественная мера степени соответствия
наблюдаемых частот m-битных
комбинаций ожидаемым частотам m-битных
комбинаций.
Контрольным распределением для статистики теста является распределение X2.
2.12.4 Описание теста
(1)
Сформировать дополненную последовательность
:
исходная последовательность дополняется
первыми m-1
битами, дописываемыми в конец.
Например,
пусть дано n
= 10 и
= 0011011101. Если m = 3, то
'
= 001101110100. Если m = 2, то
'
== 00110111010. Если m = 1, то
'
= исходной последовательности 0011011101,
(2)
Определить частоты всех возможных
перекрывающихся m-битных
блоков, всех возможных перекрывающихся
(m-1)-битных
блоков и всех возможных перекрывающихся
(m-2)-битных
блоков. Пусть
- частоты m-битных
комбинаций ii…m;
- частоты (m-1)-битных
комбинаций ii…m;
, частоты (m-2)-битных
комбинаций ii…im-2.
Для приведенного выше примера, если m = 3, то (m-1) = 2 и (m-2) = 1. Частоты всех 3-битных блоков: Vooo = 0, Voo1 = 1, Vo1o = 1, Vo11 = 2, V1oo = 1, V1o1 = 2, V11o = 2, V111= 1. Частоты всех возможных (m-1)-битных блоков: Voo = 1, Vo1 = 3, V10= 3, V11 = 3. Частоты всех (m-2)-битных блоков: V0 = 4, V1 = 6.
(3) Вычислить:
Для приведенного выше примера,
(4) Вычислить:
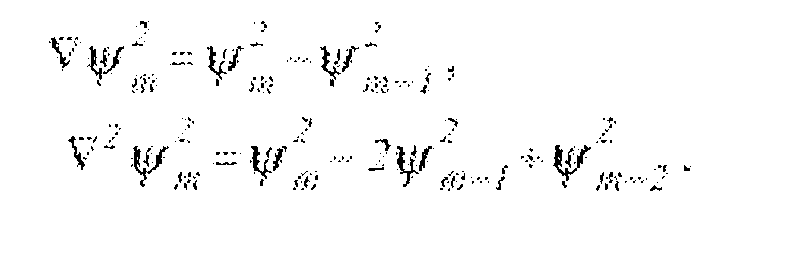
Для приведенного выше примера,
Для приведенного выше примера,
2.12.5 Решающее правило (при 1% уровне допуска)
Если вычисленное значение P-value < 0.01, то делается вывод, что последовательность не является случайной. В противном случае делается вывод, что последовательность является случайной.
2.12.6 Вывод и интерпретация результатов теста
Так как значение P-value, полученное в п. 2.12.4, > 0.01 (P-valuel = 0.808792 и Р-value2 = 0.670320), делается вывод, что последовательность является случайной.
Заметим,
что если бы значения
были бы большими, это означало бы
неравномерность m-битных
блоков.
2.12.7 Рекомендации по входным размерам
Рекомендуется
выбирать такие тип, что
.
2.12.8 Пример
(вход)
= 1,000,000 бит двоичного представления е
(вход) m=2,n= 1000000 =106
(вычисления) #0s= 499971;#1s= 500029
#OOs == 250116;#01s=#10s==249855; #11s = 250174
(вычисления) 
=0.343128;
=0.003364;
=0.000000
(вычисления) 
=0.339764;
=0.336400
(выход) Р-value1 = 0.843764; P-value2 = 0.561915
(вывод)
Так как и Р-value1, и P-value2
0.01, последовательности
принимаются случайными по обоим тестам.