2.11.6 Вывод и Интерпретация Результатов Теста

Так как P-value полученная на шаге 7 в Разделе 2.10.4>0.01 (P-value = 0.949310), делается вывод, что последовательность случайна.

Обратите внимание, если бы P-value было < 0.01, это бы означало, что рассматриваемые частотные отсчёты Т; содержащиеся в r>i ячейках отличаются от ожидаемых значений; предполагается, что распределение частот Т; (в DI ячейках) должны быть пропорциональны рассчитанным л,, как показано в шаге (6) Раздела 2.11.5.

2.11.7 Рекомендации По Входным Величинам

Выбирайте n >10⁶. Величина М должна быть в интервале 500 < М < 5000, и N >200 , для того, чтобы величина x² имела действенное значение.

2.11.8 Пример

(вход) е = "первые 1,000,000 двоичных цифр в раскрытии е "

(вход) n 1000000 =106, М=1000

(вычисляем) v0 = 11; v1 = 31; v2 = 116; v3 = 501; v4 = 258; v5 = 57; v6 = 26

(вычисляем) x² (obs) = 2.700348 (выход) P-value = 0.845406 (заключение) Т.к. P-value > 0.01, принимаем, что последовательность случайна.

3.11 Тест линейной сложности

Этот тест использует линейную сложность для проверки на случайность. Концепция линейной сложности имеет отношение у. известной части многих генераторов ключевого потока, а именно к линейным регистрам с циклическим сдвигом (ЛРЦС). Это регистр длиной L, который состоит из L элементов задержки, каждый из которых имеет один вход и один выход. Если начальное состояние ЛРЦС - (), тогда на выходе имеем последовательность (), удовлетворяющую следующей рекуррентной формуле для j > L

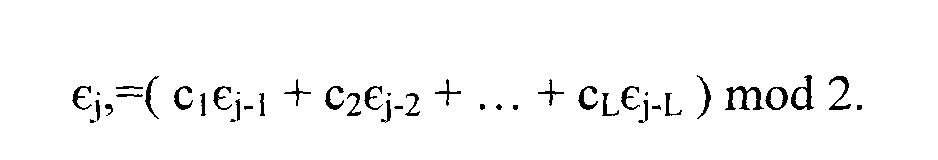
ci,..., CL - коэффициенты связующего полинома, относящегося к данному ЛРЦС. ЛРЦС должен генерировать данную бинарную последовательность, если эта последовательность является выходной для ЛРЦС с некоторым начальным состоянием. Для данной последовательности s" = (), её линейная сложность L(s") определяется как длина самого короткого ЛРЦС, генерирующего s" как первые свои п элементы. Возможность использования характеристики линейной сложности для проверки случайности основывается на алгоритме Берлекампа - Массея, обеспечивающем эффективный способ вычисления конечных строк.

Если бинарная n-последовательность s" является действительно случайной, имеют место формулы [2] для среднего u.n = EL(s") и дисперсии =Var(L(s")') линейной сложности L(s")

= Ln , если п-последовательность s" действительно случайна. Пакет Crypt-X [1] предполагает, что отношение (Ln - близко к стандартной нормальной переменной, поэтому соответствующее значения Р - value могут быть найдены из функции нормальной ошибки. Действительно, Густафсон и др. [1] (стр.693) утверждают, что «для больших n, L(s") распределено приблизительно нормально с средним n/2 и дисперсией 86/81 раз, что для

и ) 81

нормальной стандартной статистической величины z=(L(sⁿ)-Это абсолютно

неверно. Даже средняя величина р,п не ведёт себя в точности асимптотически как п/2, и в виду ограниченности дисперсии эта разница становится существенной. Более того, вероятность больших отклонений лимитирующего распределения намного больше, чем у стандартного нормального распределения.

Асимптотическое распределение отношения (L_n-_n)/_nв соответствии с последовательностью чётных и нечётных значений n является дискретной случайной переменной, полученной смешиванием двух геометрических случайных переменных ( одна из которых принимает только отрицательные значения). Строго говоря, асимптотическое распределение как таковое' не существует. Случаи с чётными и нечётными значениями n должны рассматриваться! отдельно с двумя разными возникающими лимитирующими распределениями.

Исходя из этого факта, применяется следующая последовательность статистических данных

Эти статистические данные, принимающие только целые значения, сходятся по распределению к случайной переменной Т. Это лимитирующее распределение ассиметрично

справа. Пока Р(Т=0) = , для k==l ,2,...

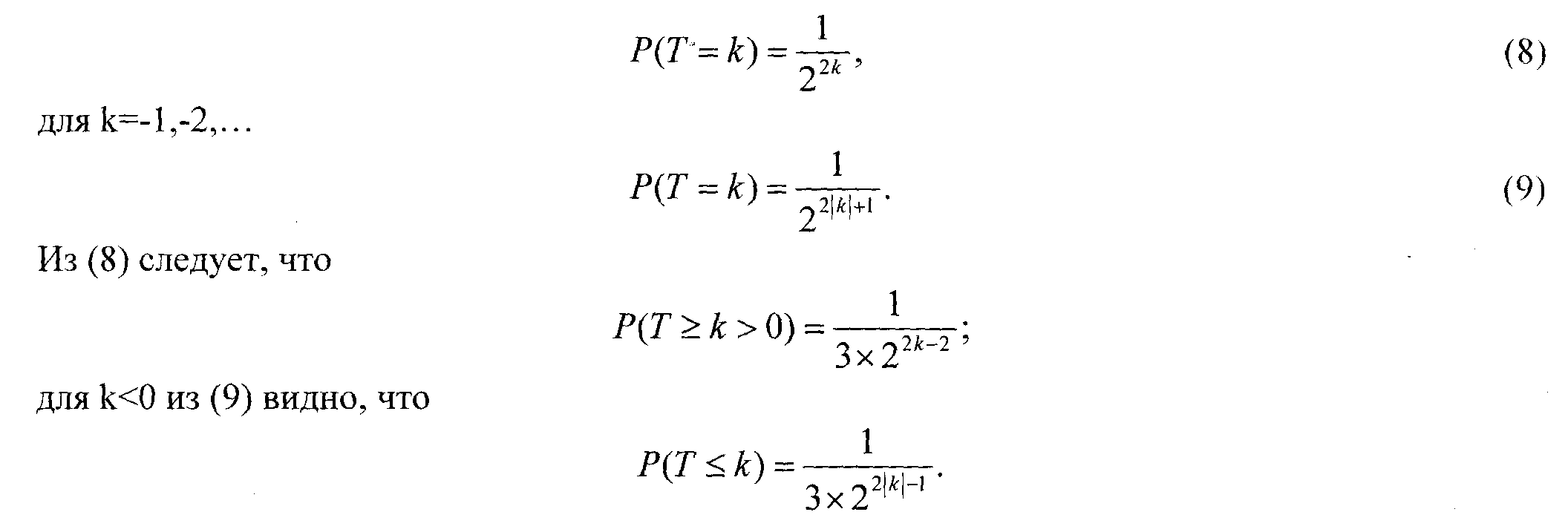
Таким образом P-value относящееся к рассматриваемому значению Tobs может быть получена следующим путём. Пусть k = +1. Тогда P-value равно

В виду дискретной природы этого распределения и невозможности достижения единообразного распределения для P-value, может быть применена стратегия, использовавшаяся в других тестах с такой же ситуацией. А именно, разбиение строки длиной п, n=MN, на N подстрок длиной М. Для каждого теста, основанного на линейной сложности статистических данных (6), рассчитываются Тм в пределах j-ой подстроки длиной М. выбираются К+1 класса ( зависящие от М ). Для каждой из этих подстрок, определены частоты , для значений Тм принадлежат одному из К+1 выбранных классов, = N. Удобно выбирать классы с концевыми значениями дробного значения.

Теоретические вероятностей каждого из этих классов определяются из (8) и (9).,

Для этого М должно быть достаточно большим, чтобы лимитирующее распределение, данное;

в (8) и (9) обеспечивало приемлемое приближение. М должно превышать 500. Рекомендуется) выбрать М, такое, что 500 < М $ 5000.

Частоты объединяются значением %1

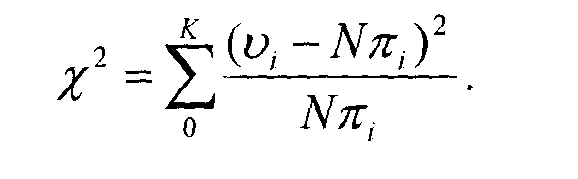
которое, согласно гипотезе случайности, имеет приблизительно X²- распределение с 11 степенями свободы. P-value определяется

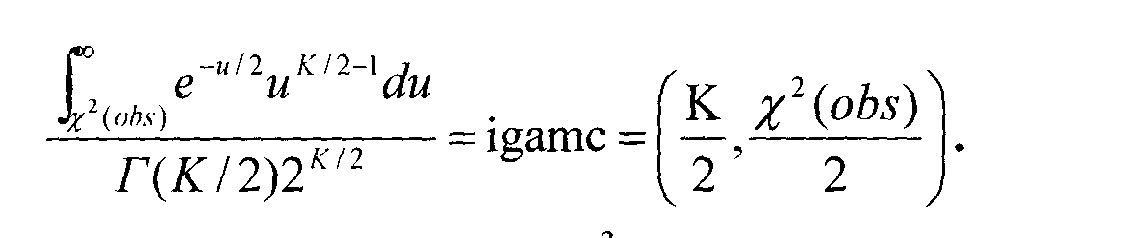
Как и раньше, имеется условие на использование X² -приближения

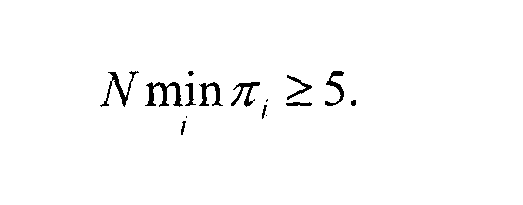
Для достаточно больших значений М и N следующие классы (К=6) являются адекватными {Т-2.5}, {-2.5 < Т -1.5}, {-1.5 < Т -0.5}, {-0.5 < Т 0.5}. {0.5 < Т 1.5}, {1.5 < Т 2.5} и {Т>2.5}.

Вероятности этих классов = 0.01047 , ₁, = 0.03125, ₂ = 0.125 , ₃ = 0.5, ₄= 0.25 , ₅ = 0.0625 , ₆ = 0.020833. Эти вероятности в значительной степени отличаются от

полученных из нормального приближения, для которых значения следующие: 0.0041, 0.0432, 0.1944, 0.3646, 0.2863, 0.0939, 0.0135.

Ссылки для Теста

[1] H. Gustafson, E. Dawson, L. Nielsen, and W. Caelli (1994), "A computer package for measuring the strength of encryption algorithms," Computers and Security. 13, pp. 687-697.

[2] A. J. Menezes, P. C. van Oorschot, and S, A. Vanstone (1997), Handbook of Applied CrvutoeraDhv. CRC Press, Boca Raton. FL.