2.1 Частотный тест (на монотонность бит)

2.1.1 Назначение теста

Данный тест рассматривает пропорциональность количества нулей и единиц для всей последовательности. Назначение этого теста состоит в определении того, является ли количество единиц и нулей в тестируемой последовательности приблизительно таким же, каким оно должно быть в действительно случайной последовательности. Тест оценивает близость доли единиц к ½, то есть число единиц и нолей в последовательности должно быть приблизительно одинаковым. Все последующие тесты зависят от прохождения этого теста; нет оснований указывать, что протестированная последовательность является неслучайной.

2.1.2 Исходные данные

• n- длина последовательности бит.

•  = ₁, ₂, ..., _n - последовательность битов, сгенерированная RNG или PRNG

2.1.3 Тестовая статистика и исходное распределение

S_obs: абсолютное значение суммы значений Xi где Хi = 2,-1 = ±1) в

последовательности, делённое на квадратный корень длины последовательности.

Исходное распределение тестовой статистики - полу-нормальное (для больших n).

Примечание: Если z (где z =S_obs /√2) распределена по нормальному закону, тогда распределение |z| - полу-нормальное.

Если последовательность случайная, тогда +1 и -1 будут иметь тенденцию уравновешивать друг друга, так что тестовая статистика будет приблизительно около 0. Если присутствует слишком много единиц или слишком много нулей, тогда тестовая статистика будет иметь тенденцию быть больше нуля.

2.1.4 Описание теста

1. Преобразование к ±1: нули и единицы входной последовательности () преобразуются к значениям -1 и +1 и суммируются для получения S_n = X_i + Х₂ + ... + Х_n, где X_i = 2_i -1.

2. Вычисление статистического значения S_obs = |Sn|/ √n

3. Вычисление Р-value = erfс (S_obs / √2), где erfс - комплементарная функция ошибки:

2.1.5 Правило принятия решения (на 1%-ом уровне)

Если вычисленное значение Р-value < 0.01, то следует сделать заключение, что последовательность не является случайной. В противном случае, следует сделать заключение, что последовательность случайная.

2.1.6 Заключение и интерпретация результатов теста

В случае, когда P-value мало (<0.01), это вызвано большими значениями Sn или Sobs. Большие положительные значения Sn свидетельствуют о присутствии слишком большого числа единиц в последовательности, а слишком большие отрицательные значения - слишком большого числа нулей.

2.1.7 Рекомендуемый размер входной последовательности

Рекомендуется, чтобы каждая тестируемая последовательность состояла как минимум из 100 битов (то есть, n 100)

2.1.8 Пример

(вход) = 11001001000011111101101010100010001000010110100011 00001000110100110001001100011001100010100010111000

(вход) n = 100

(обработка) S₁₀₀ =-16

(обработка) S_obs =1.6

(результат) P-value = 0.109599

(заключение) Поскольку P-value >.0.01, последовательность следует принять как случайную.

3.1 Техническое описание

Первичный тест строится на нулевой гипотезе: в последовательности независимых одинаково распределённых случайных переменных Бернулли (Х или , где Х = 2-1, и Sn=Xi+...+Xn= 2(i+...n ) – n), вероятность единиц равняется ½. По классической теореме. Де Муивра-Лапласа, для достаточно большого числа испытаний, распределение биномиальной суммы, нормированное на √n, распределено достаточно близко по нормальному закону. Данный тест использует это приближение для оценки близости доли единиц к ½. Все последующие тесты базируются на том, будет ли пройден данный тест.

Тест получен из известного передела Центральной Предельной Теоремы для случайного шага, Sn=X1+... +Хn. Согласно Центрально Предельной Теореме,

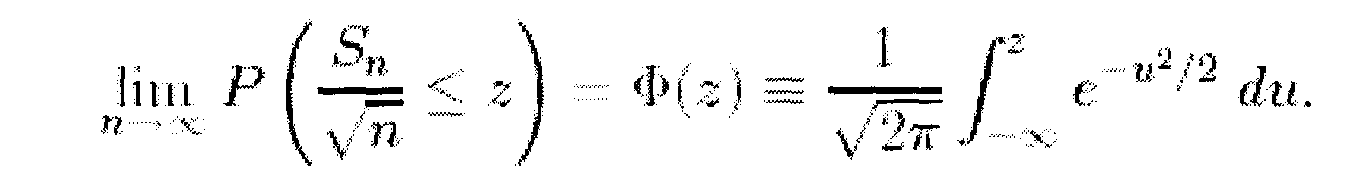
Этот классический результат служит основанием для простейшего теста на случайность. Он подразумевает что, для положительных z,

Согласно тесту, базируемому на статистике s = |Sn|√n оцените наблюдаемое значение

а затем рассчитайте соответствующее P-value, равное

Здесь erfc - это комплементарная функция ошибки:

Ссылки для теста

[1] Кэй Лэй Чанг, Элементарная Теория Вероятности со Стохастическими Процессами. Нью-Йорк: Springer-Verlag, 1979 (особенно стр 210-217).

[2] Джим Питман, Вероятность. Нью-Йорк: Springer-Verlag, 1993 (особенно стр 93-108).