4.3 Определение устойчивости линейной части системы по критерию Михайлова
Для
того чтобы определить, устойчива ли
система по критерию Михайлова, необходимо
построить годограф амлитудо-фазовой
характеристики. Для того чтобы построить
годограф, заменим в характеристическом
уравнении p
на i·ω.
И разделим действительную и мнимую
части
соответственно. При этом мнимую часть
будем откладывать на оси ординат, а
действительную – на оси абсцисс. По
критерию, САР устойчивая в том случае,
если годограф Михайлова при изменении
частоты от 0 до бесконечности повернется
против часовой стрелки, начиная с
вещественной оси на число квадрантов,
равное порядку характеристического
уравнения последовательно проходя эти
квадранты.
Запишем характеристическое уравнение:
График годографа Михайлова построим в координатах:
M(iω)=U(ω)+iV(ω)
Н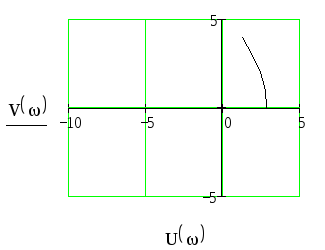
а
рисунке 5 представлен общий вид годографа
Михайлова.
Рисунок 5 – Общий вид годографа Михайлова
По данному виду годографа Михайлова, можем сделать вывод, что система не устойчива, так как годограф Михайлова не проходит 4 квадранта и не уходит в бесконечность.
4.4 Критерий Шур-Кона
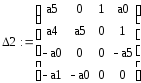
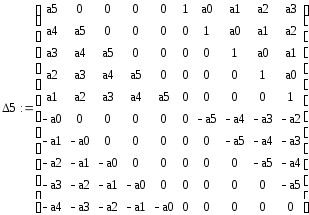
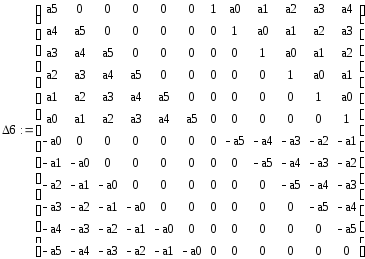
Система устойчива в том случае, если все чётные определители положительны, а нечётные отрицательны.
С помощью программы Маткад получим дискретную функцию системы и посчитаем систему на устойчивость.
Система устойчива.
Построим переходный процесс для дискретной системы, с помощью программы Матлаб.
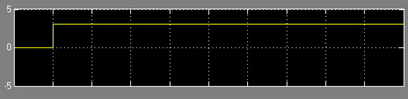
5 Построение лачх системы и ее анализ
Построим ЛАЧХ САУ солнечной батареей космического спутника. Для построения ЛАЧХ, нам необходимо разомкнуть систему. На рисунке 6 представлена разомкнутая структурная схема САУ солнечной батареей космического спутника.
W1(p)
W2(p)
W3(p)
W4(p)
Рисунок 6 – Разомкнутая структурная схема САУ солнечной батареей космического спутника
Общая передаточная функция разомкнутой системы имеет вид:
Для построения ЛАЧХ разомкнутой передаточной функции проведем Z – преобразование по следующей формуле:
С
помощью программы MatLab
найдем
от
передаточной функции Wобщ.р.(p):
W=tf([2.9],[0.06e-5 0.01e-7 0.1 1 0])
Transfer function:
2.9
-------------------------------------
6e-007 s^4 + 1e-009 s^3 + 0.1 s^2 + s
W=c2d(W,0.01)
Transfer function:
0.001163 z^3 + 0.003308 z^2 + 0.003563 z + 0.001184
---------------------------------------------------
z^4 - 0.668 z^3 - 0.3463 z^2 - 0.9858 z + 1
Sampling time: 0.01
Далее необходимо перейти к псевдочастоте. Для этого производится замена
а
затем замена
Построим ЛАЧХ по полученной передаточной функции псевдочастот в программе MatLab:
0
дБ/дек
-20
дБ/дек
Magnitude
(dB) Phase
(deg) Frequency
(rad/sec)
-40
дБ/дек
10
0
-10
-20
-30
-90
-180
-270
-360
10-2
10-1
100
101
ΔL
Δφ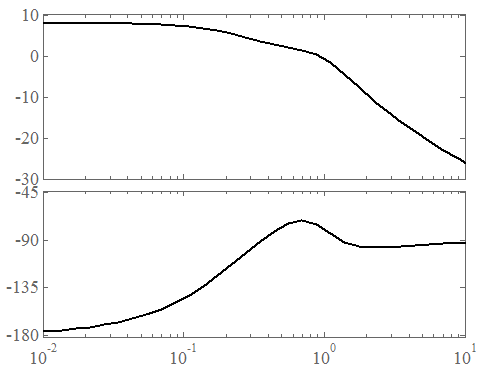
Рисунок 7 – ЛАЧХ и ЛФЧХ САУ солнечной батареей космического спутника.
По данному рисунку видно, что в рассматриваемой системе существуют запасы устойчивости по фазе 5 дБ и по амплитуде -155 дек.
Аппроксимируем ЛАЧХ стандартными наклонами и составим передаточную функцию:
Тогда передаточная функция имеет следующий вид:
6 ПОСТРОЕНИЕ ЖЛАЧХ СИСТЕМЫ, ЛАЧХ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, имеющей желаемые (требуемые) статические и динамические свойства.
Строится желаемая ЛАЧХ на основании требований к системе.
Низкочастотная асимптота ЛАЧХ разомкнутой системы определяет статические свойства.
Если
передаточная функция разомкнутой
системы имеет передаточный коэффициент
и
порядок астатизма
,
удовлетворяющий требованиям, то
низкочастотная асимптота желаемой ЛАЧХ
является низкочастотной асимптотой
неизменной части системы.
Среднечастотная асимптота ЛАЧХ разомкнутой системы и её сопряжение с низкочастотной определяют динамические свойства системы – устойчивость и показатели качества переходной характеристики.
Построение
среднечастотной асимптоты желаемой
ЛАЧХ начинают с выбора частоты среза
Для
этого используют номограмму Солодовникова.
Она определяет зависимость перерегулирования
и
времени регулирования
от
максимума
вещественной частотной характеристики
замкнутой системы, причем время
регулирования
дано в виде в виде функции частоты среза
.
По заданному значению перерегулирования
определяют значение
.
Затем
по
определяют
соотношения между
и
Высокочастотная асимптота желаемой ЛАЧХ (ЖЛАЧХ) мало влияет на свойства системы.
Поэтому
ее выбирают так, чтобы корректирующее
устройство было возможно более простое.
Это достигается при совмещении
высокочастотных асимптот характеристик
и
.
Если совмещение не удается, то
высокочастотная асимптота
должна иметь тот же наклон, что
и
высокочастотная асимптота
.
Так как система является дискретной,
то необходимо определить запретную
зону, для этого найдем рабочую точку и
отметим ее на ЛАЧХ.
где
– скорость изменения входного сигнала,
кг/с;
– ускорение
изменения входного сигнала, кг/с2;
– точность
прохождения сигнала.
Зададим значения, принимая, что за один опрос датчика (0.7с) может произойти изменение значение входного сигнала на 2 C0. Ускорение изменения входного сигнала обычно для промышленных систем автоматики принимают как сотую часть от скорости изменения входного сигнала.
С0/с
С0/с2
δ = 0.01 – допустимая ошибка.
Значение частоты рабочей точки
с-1
Расчет координаты рабочей точки.
дБ.
Таким образом, рабочая точка
А(0.01, 89).
Через
полученную точку
проводим прямую с наклоном минус
20
дБ/дек. Эта прямая является верхней
границей запретной зоны.
Соответственно желаемая ЛАЧХ должна проходить выше этой зоны.
По номограмме Солодовникова (рисунок 8) по заданным в техническом задании желаемому перерегулированию 25% и времени регулирования 15c определяем частоту среза и колебательность.
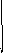
Рисунок 8 – Номограмма Солодовникова
Перейдем к псевдочастоте.
,
,
где Т0=0.01 с – период дискретизации
По заданной колебательности М=1.1 найдем среднечастотную область построения ЖЛАЧХ. Границами для амплитуды этой области соответствуют значения бесконечности.
Построить ЛАЧХ корректирующего устройства можно с помощью графического вычитания реальной ЛАЧХ из желаемой ЛАЧХ, то есть используется последовательная коррекции.
Наклон ЖЛАЧХ в среднечастотной области должен быть -20 дБ/дек, через частоту среза в этой области проводим прямую с наклоном -20 дБ/дек. В высоко-частотной области ЖЛАЧХ сопрягается с исходной ЛАЧХ, то есть будет иметь такие же наклоны. Низкочастотная область не имеет большого значения, поэтому достраивается произвольно, в данном случае – с тем же наклоном, что и ЛАЧХ для упрощения корректирующего устройства.
ЖЛАЧХ, ЛАЧХ КУ представлены на рисунке 9.
-20
Дб/дек
-20
Дб/дек
Lку 89
0
Дб/дек
20
Дб/дек
0
Дб/дек 79
+40
Дб/дек
LР
0
Дб/дек
Lж
102
Запишем передаточную функцию желаемой ЛАЧХ, ЛАЧХ последовательного корректирующего устройства:
Рассчитаем числовые значения для WЖ(p):
Рассчитаем числовые значения для передаточной функции корректирующего устройства:
7 РАЧЕТ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА. ВОЗМОЖНОСТЬ ИСПОЛЬЗОВАНИЯ ДИСКРЕТНОГО КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА
7.1 Расчет аналогового корректирующего устройства
Для коррекции в системе применяется корректирующее устройство (КУ) с опережением и отставанием по фазе последовательного типа. Корректирующее устройство можно включить между различными элементами исходной системы.
При выборе места включения руководствуются значением вносимой устройством погрешности. Наиболее предпочтительным вариантом является установка корректирующего устройства в электрическую цепь после микропроцессора.
Схема корректирующего устройства, представленная на рисунке 12, имеет вид:
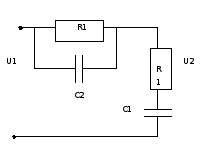
Рисунок 10 - Схема корректирующего устройства
Передаточная функция второго участка имеет вид:
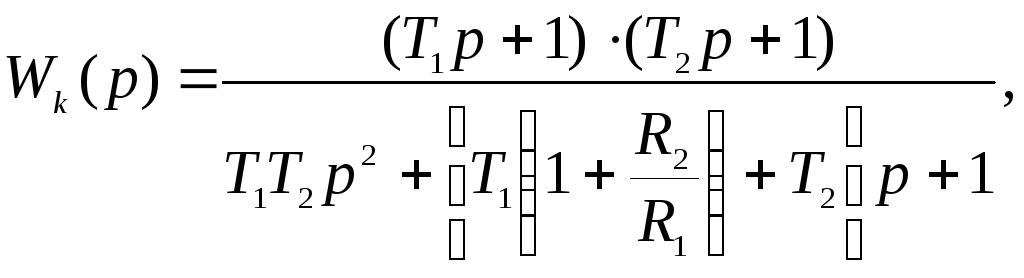
где
Рассчитаем передаточную функцию первого участка корректирующего устройства, нам известно, что Т1=5 с, а Т2=1, следовательно зададимся следующими значениями для R1=6 МОм, R2=10 МОм.
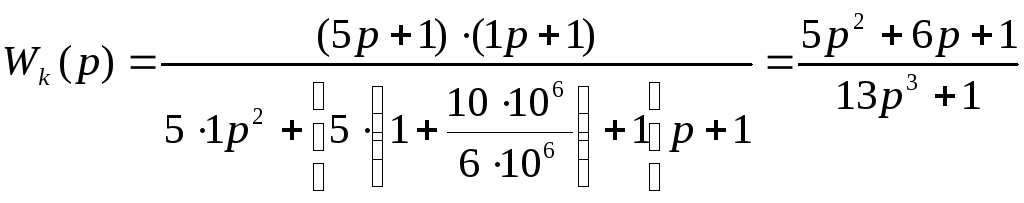
Схема включения КУ в систему управления представлена на рисунке 11.
МП
ШД
СБ
КУ
ДУП
МП – микропроцессор; КУ – корректирующее устройство; ШД – шаговый двигатель; СБ – солнечная батарея; ДУП- датчик угла поворота
Рисунок 11 - Включение корректирующего устройства в систему автоматического управления