4. Расчет устойчивости системы

4.1 С учетом передаточных функций всех элементов составляем структурную схему системы:

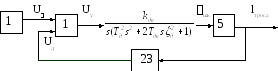
Рисунок 3- Структурная схема системы управления

U_=1- импульс напряжения от кнопки управления,

U_у=1 – импульс управления от шкафа управления,

_шк=680⁰– угол поворота ротора двигателя,

l_троса– перемещение кабины лифта,

U_ном=4,5910^-4В –номинальное напряжение выдаваемое датчиком.

U_д- напряжение выдаваемое датчиком через усилитель

С учетов всего сказанного передаточная функция всей системы принимает вид:

(9)

2. Проведем анализ устойчивости системы по критерию устойчивости Гурвица

С

(10)

оставим характеристическое уравнение системы.

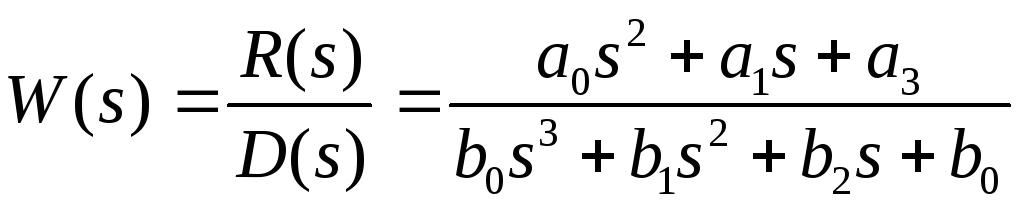
где D(s)- характеристическое уравнение системы

D(s)=23s³+1,2s² +s+0.035

Определители Гурвица примут вид

=1,288

=0,0138

1= 1

Согласно критерию система устойчива, если все определители положительны при значении коэффициента а₀>0.

О

пределители, полученные из анализа системы, положительны, следовательно, система устойчива.

4. Построение логарифмической амплитудно-частотной характеристики неизменяемой части системы и ее анализ

Передаточную функцию системы записываем в частотном виде.

(11)

К

(12)

омплексное представление передаточной функции разбиваем на реальную и мнимую части.

(13)

П

(14)

остроим ЛАЧХ системы.

-40дБ

-60дБ

Р

исунок 4- ЛАЧХ неизменяемой части системы

Анализируя полученную ЛАЧХ, можно отметить, что система имеет малый передаточный коэффициент. Это связано с тем, что система дискретна, а построение производится относительно частоты w. ПроведемZ- преобразование передаточной функции системы. Для этого выражение (9) разложим на элементарные дроби:

Представим передаточную функцию элементарных дробей в виде zпреобразований и тогда получим выражение (15).

(15)

Вводим замену s =j

П

(16)

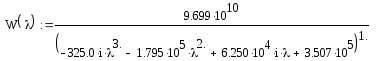
ередаточная функция системы примет вид:

С

учетом введенных изменений построим ЛАЧХ, полученной после подстановки, системы.

4. Построение желаемых логарифмических характеристик системы и корректирующего устройства системы

1. Построение ЖЛАХЧ системы

Так как система дискретна, для построения ЖЛАЧХ воспользуемся методом запретной зоны.

Необходимые показатели качества системы заданы в техническом задании:

t_р= 1,5c– время срабатывания системы

 =20%- значение пере регулирования

M==1,1-показатель колебательности системы

Определим границу запретной зоны.

Максимально допустимая ошибка системы _доп==0,004.

Максимальная скорость изменения сигнала ==1,78 –первая производная от задающего воздействия, полученная из анализа работы системы.

Максимальное ускорение изменения сигнала == 0,155 – вторая производная то задающего воздействия.

З

(17)

адающее воздействие (сигнал от кнопки) заменяется эквивалентным синусоидальным сигналом:

q = A sin_kt,

где

_к= 8–частота рабочей точки.

А==7,510^-3- рабочая амплитуда

=А_k= 1,78

=А_k²= 0,155

lg(_к)=0,903

А

(18)

1==1,5

20lg(А1)=3,522

Определим частоту среза _ср

(19)

_ср==3.63c^-1

Запретную зону определяют граничные частоты ₁=,₂=,

где h==21.

После ₂ЖЛАХЧ системы повторяет истинную ЛАЧХ. Совмещаем_ср с границей запретной зоны и от₂продолжаем ЖЛАЧХ до наклона ЛАЧХ –60дБ.

Т

(20)

аким образом, мы получили ЖЛАЧХ системы, с помощью которой можно определить ЛАЧХ корректирующего устройства:

L_ку()=W()-L_нч(),

где W_ж() –ЖЛАЧХ системы

L

_нч()- ЛАЧХ корректирующего устройства

-20дБ

60

-40дБ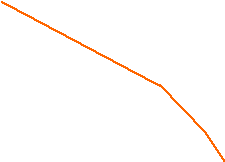

-40дБ

L1()

-20дБ

20дБ

0дБ

0дБ

W()

-10

-40дБ

0дБ

-20дБ

20дБ

L_ку()

-40дБ

0дБ

-60дБ

-80

1

10

100

0.1

0.01

0.001

1000

, c^-1

Р

Ф()

исунок 5- Логарифмические характеристики системы и корректирующего устройства

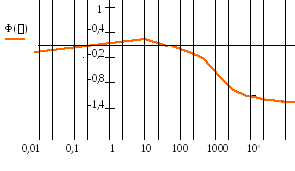
, c^-1

Р

исунок 6- Желаемая логарифмическая фазово-частотная

характеристика системы

При анализе ЛАЧХ неизменяемой части системы находим запасы устойчивости:

• по амплитуде L_ж=6 дБ,

• з

  

  апас устойчивости по фазе=0,6⁰.