1.2 Влияние изменения параметров на характеристики системы

Для исследования влияния изменения параметров двухмассовой упругой системы на характеристики этой системы воспользуемся полной схемой, изображенной на рисунке 1.5.

Рисунок 1.5 – Полная схема двухмассовой упругой системы

При исследовании системы оцениваем влияние параметров:

• коэффициента жесткости С₁₂;

• момента инерции механизма J₂;

• коэффициента демпфирования ₁₂.

Коэффициент жесткости вычисляется следующим образом:

где=₁–₂– угол скручивания, М₁₂– момент упругого взаимодействия.

Сначала принимаем J₂=J₁= 0,0042 Нм.

С помощью программного комплекса SystemViewстроим переходные характеристики при= 1 (рисунок 1.6),= 2 (рисунок 1.7),= 0,5 (рисунок 1.8).

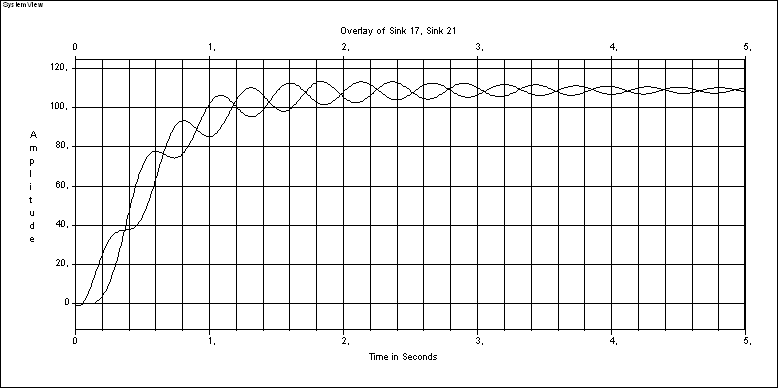
Рисунок 1.6 – Переходный процесс при С₁₂= М_HиJ₂=J₁

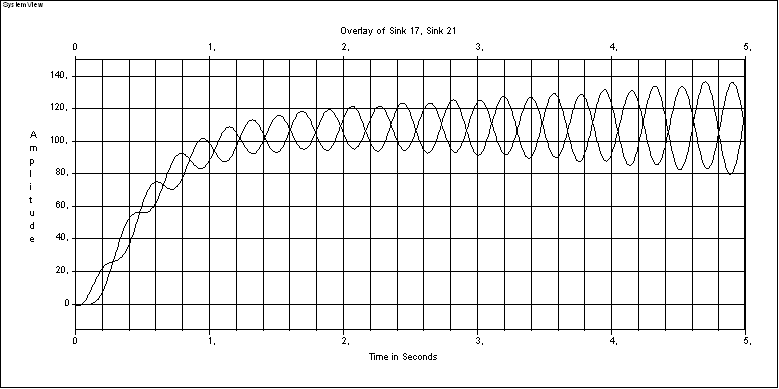
Рисунок 1.7 – Переходный процесс при С₁₂= 2М_HиJ₂=J₁

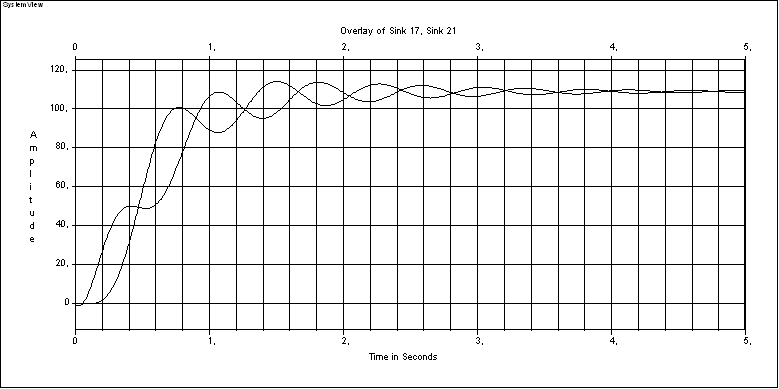
Рисунок 1.8 – Переходный процесс при С₁₂= М_H/2 иJ₂=J₁

Принимаем J₂=J₁/2 = 0.021 Нм и строим переходные характеристики при= 1 (рисунок 1.9),= 2 (рисунок 1.10),= 0,5 (рисунок 1.11).

Рисунок 1.9 – Переходный процесс при С₁₂= М_HиJ₂=J₁/2

Рисунок 1.10 – Переходный процесс при С₁₂= 2М_HиJ₂=J₁/2

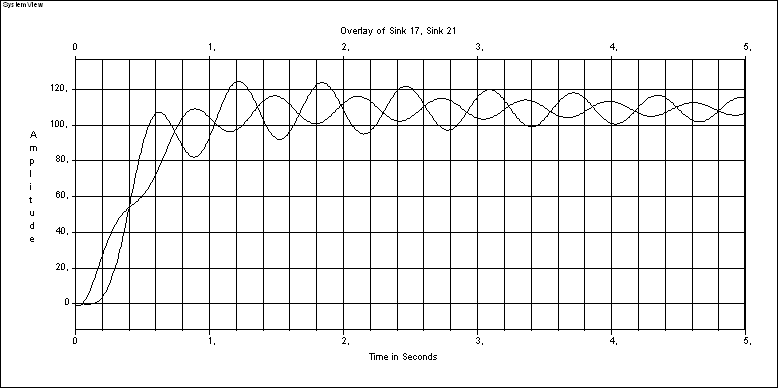
Рисунок 1.11 – Переходный процесс при С₁₂= М_H/2 иJ₂=J₁/2

Принимаем J₂= 2J₁= 0.084 Нм и строим переходные характеристики при= 1 (рисунок 1.12),= 2 (рисунок 1.13),= 0,5 (рисунок 1.14).

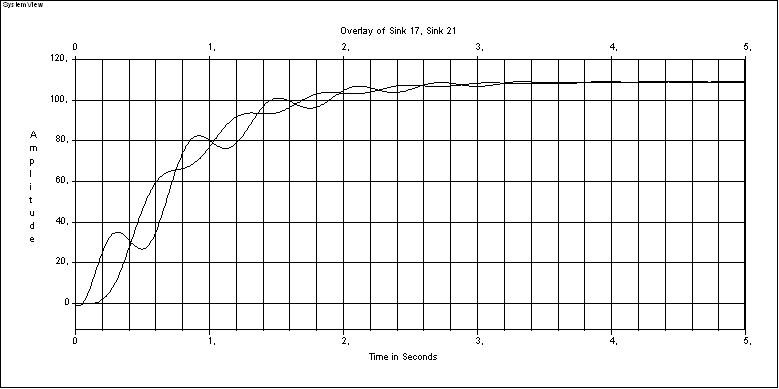
Рисунок 1.12 – Переходный процесс при С₁₂= М_HиJ₂= 2J₁

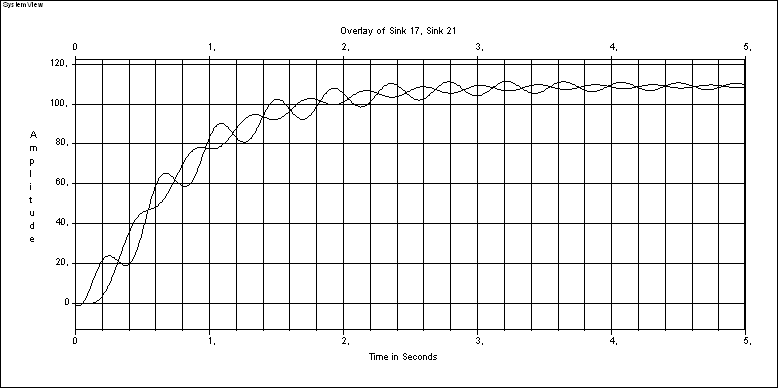
Рисунок 1.13 – Переходный процесс при С₁₂= 2М_HиJ₂= 2J₁

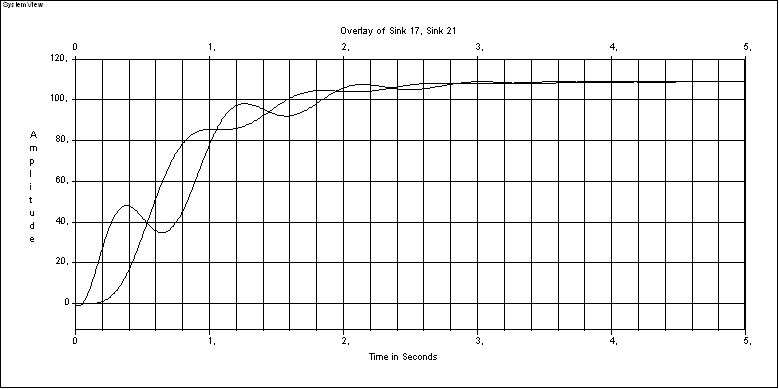
Рисунок 1.14 – Переходный процесс при С₁₂= М_H/2 иJ₂= 2J₁

Введем в схему демпфирование, которое должно уменьшить колебания и привести к установлению процесса.

Величина коэффициента ₁₂вычисляется по формуле:

где М_в.т.– момент вязкого трения,₁-₂возьмём равным 4.

Таким образом

Демпфирование введем в схему с большим колебательным процессом при С₁₂= 2М_НиJ₂=J₁(рисунок 1.7).

После ввода демпфера получается процесс, изображенный на рисунке 1.15.

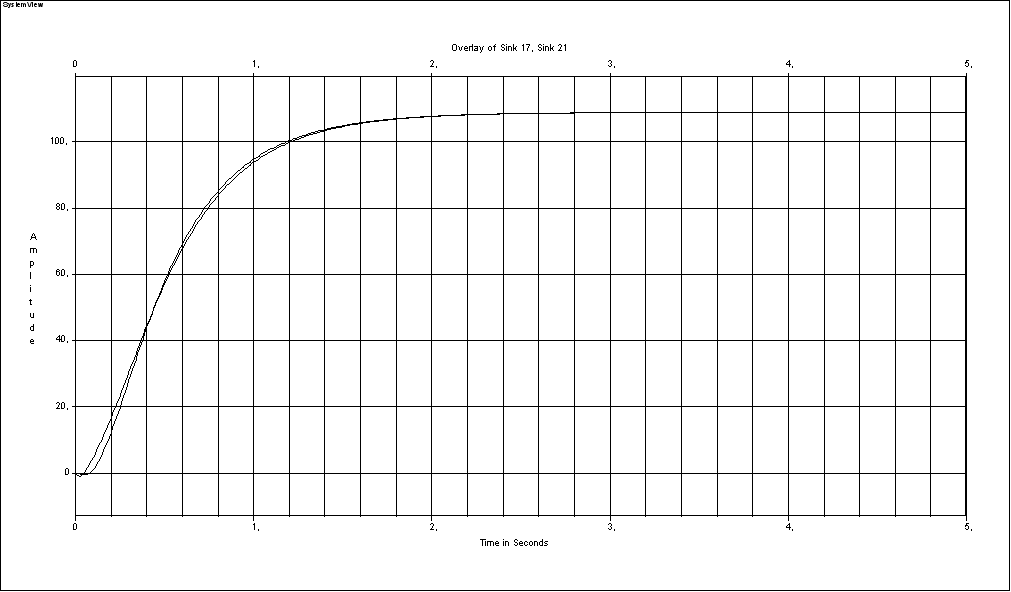
Рисунок 1.15 – Переходный процесс при введении демпфера

1.3 Выводы по первой главе

В данной главе были получены характеристики заданного двигателя и проведены исследования по влиянию изменений параметров двухмассовой системы на её характеристики. Из полученных графиков, можно сделать выводы:

• с увеличением коэффициента жёсткости колебания в системе возрастают;

• при маленьком коэффициенте жёсткости и моменте инерции, система наиболее устойчива;

• при большом моменте инерции система быстрее приходит в устойчивое состояние;

• введение в систему демпфера значительно повышает её устойчивость.

2 Выбор закона регулирования. Определение оптимальных параметров настройки

При выборе регулятора воспользуемся установленными заданием требованиями, сведенными в таблице 2.1.

Таблица 2.1 – Исходные данные для выбора типа регулятора

K	Т, с	τ, с	tp, c	Ψ, %	Δxдоп	yв	х1доп
3,2	100	25	250	55	10	12	25

где K_об-коэффициент передачи объекта,

Т_об-постоянная времени объекта,

τ_об-время запаздывания объекта,

t_p-допустимое время регулирования,

Ψ -допустимое перерегулирование,

Δx_доп-допустимое остаточное отклонение,

y_в- максимально возможное возмущение по нагрузке,

Δx_доп-максимальное допустимое динамическое отклонение.

Исходя из значения Ψ, определяем, что у нас процесс с минимальной квадратичной площадью отклонения параметра.

Тип регулятора определяется отношением /Т.

В нашем случае /Т = 25/100 = 0,25, следовательно, регулятор непрерывный.

Пользуясь исходными данными, определяем величину динамического коэффициента регулирования R_д, при котором может быть получено требуемое значение динамического отклонения.

Зная тип переходного процесса, определяем тип регулятора в зависимости от значений τ/Т и R_д(по графику на рисунке 2.1). Из графика видно, что в данном случае имеет место П-закон регулирования.

Далее необходимо проверить регулятор на величину остаточного отклонения регулируемой величины от заданного значения и на соответствие фактического времени регулирования заданному.

Из графика на рисунке 2.2 определим отношение t_p/τ и выразим отсюда t_p.

t_p/τ = 8,t_p = 200, что не больше заданного значения.

Из графика на рисунке 2.3 определим допустимое перерегулирование δ_доп, а исходя из него и остаточное отклонение Δx.

δ_доп=0,2,

.

Полученное значение Δx < Δx_доп, следовательно закон выбран правильно.

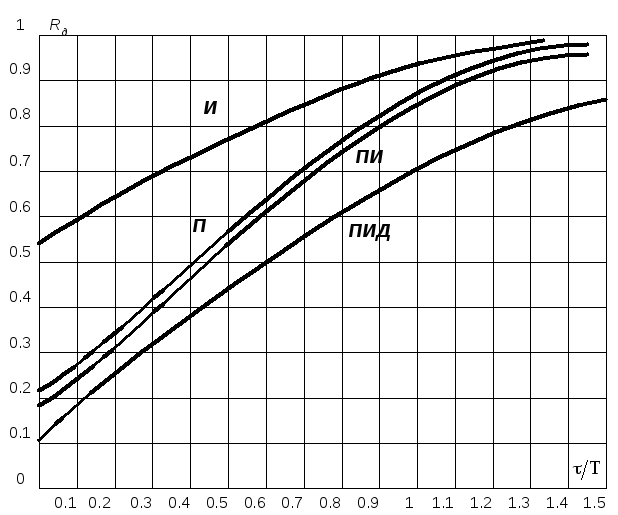
Рисунок 2.1 – График для выбора закона регулирования для переходного процесса с минимальной квадратичной площадью отклонения

Рисунок 2.2 – График для проверки на соответствие времени регулирования

для переходного процесса с минимальной квадратичной площадью отклонения

апериодический

с 20% перерегулированием

с минимальной квадратичной площадью отклонения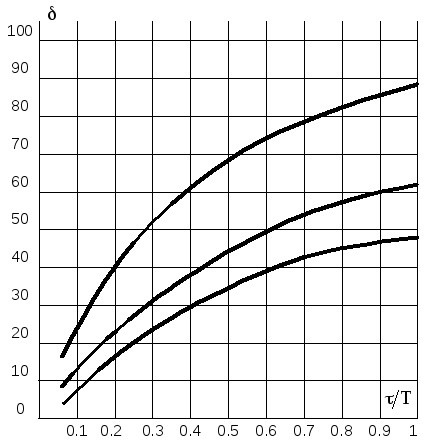

Рисунок 2.3 – График для поверки регулятора на соответствие остаточного отклонения регулируемой величины

Схема, реализующая П-регулятор выглядит следующим образом для идеального регулятора (рисунок 2.4)

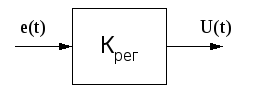
Рисунок 2.4 - Схема идеального П-регулятора

Рассчитаем параметры настройки регулятора:

К_рег=.

График регулятора представлен на рисунке 2.5.

Рисунок 2.5 – График регулятора