
курсовая работа / для курсача по ТАУ / rgz
.pdf
звеньев, в этом случае W (s) и Wo.c (s) определяются в зависимости от вида со-
единения звеньев (определение передаточных функций отдельных звеньев рас- смотрено ранее).
Передаточная функция разомкнутой системы (разомкнутого контура) оп- ределяется следующим соотношением:
W p(s) = W (s)×Wo.c (s). |
(1) |
Далее определяем амплитудно-фазовую частотную характеристику, под- ставляя в (1) s = jω , и находим логарифмические амплитудную и фазовую час-
тотные характеристики по соотношениям, приведенным выше.
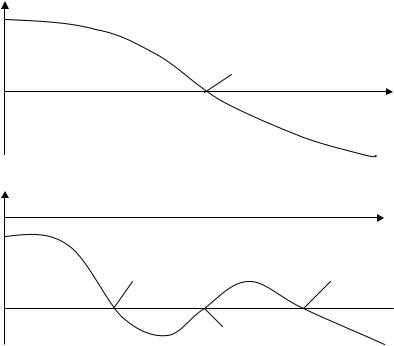
Частотные характеристики устойчивой системы приведены на рис. 2.
L(ω)
1
|
|
|
|
|
lgω |
0 |
|
|
|
|
|
ϕ(ω) |
ωср |
|
Lзап |
||
|
|||||
|
|||||
|
|
|
|
lgω |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
ωпер |
2 |
ϕзап |
|
|
|
|
|
|
|
|||
-π |
|
|
|
|
|
Рис. 2. Логарифмические частотные характеристики устойчивой системы
В общем случае, когда разомкнутая система неустойчива и имеет K кор- ней справа от мнимой оси, замкнутая система будет устойчива, если разность положительных (+) и отрицательных (–) переходов фазовой характеристики ра-
зомкнутой системы через прямую « −π» (рис. 3.) равна K 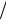 2 при значениях час- тот ω , при которых L(ω) > 0.
2 при значениях час- тот ω , при которых L(ω) > 0.
В общем случае, когда разомкнутая система неустойчива и имеет K кор- ней справа от мнимой оси, замкнутая система будет устойчива, если разность положительных (+) и отрицательных (–) переходов фазовой характеристики ра- зомкнутой системы через прямую « −π» (рис. 3.) равна K  2 при значениях час-
2 при значениях час-
тот ω , при которых L(ω) > 0.
L(ω)
ω ср |
lgω |
0
ϕ(ω)
lgω
0
− |
− |
−π
+
Рис. 3. Логарифмические частотные характеристики устойчивой замкнутой системы, когда разомкнутая система неустойчива
6.2. Алгебраический критерий устойчивости (критерий Гурвица)
Алгебраические критерии устойчивости позволяют проверять линейные системы и их элементы на устойчивость по соотношениям коэффициентов ле- вой части уравнения, записанного в форме “вход-выход”.
Критерий Гурвица удобно применять когда система, описывается уравнением не выше четвертой степени. В этом случае условие устойчивости получается в виде общего соотношения.
Для уравнения второй степени
a |
|
d 2 y |
+ a |
dy |
+ a |
|
y = b |
|
2 |
dt2 |
1 |
dt |
|
0 |
2 |
критерий устойчивости Гурвица имеет вид:
a0 > 0; a1 > 0;
Для уравнения третье степени
d 2u |
+ b |
du |
+ b u |
dt2 |
1 |
dt |
0 |
a2 |
> 0 . |
|
|
a |
d 3 y |
+ a |
d 2 y |
+ a |
dy |
+ a |
|
y = b |
d 3u |
+ b |
d 2u |
+ b |
du |
+ b u |
3 |
dt3 |
|
2 dt2 |
1 |
dt |
|
0 |
3 |
dt3 |
2 |
dt2 |
1 |
dt |
0 |
критерий Гурвица можно записать в виде: |
|
a0 > 0; a1 > 0; a2 |
> 0; a3 > 0; |
a1a2 − a0a3 |
> 0. |
Для уравнения четвертой степени |
|
a |
d 4 y |
+ a d 3 y |
+ a |
d 2 y |
+ a dy |
+ a |
|
y = b |
|
4 dt4 |
3 dt3 |
|
2 dt2 |
1 dt |
|
0 |
4 |
критерий Гурвица имеет вид
a0 > 0; a1 > 0; a2 > 0;
d 4u |
+ b |
d 3u |
+ b |
d 2u |
+ b |
du |
+ b u |
dt4 |
3 |
dt3 |
2 |
dt2 |
1 |
dt |
0 |
a3 |
> 0; |
a4 |
> 0; |
|
|
|
|
|
|
|
|
|
|
|
|
a a |
a |
3 |
− a2a |
4 |
− a a2 |
> 0. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
0 |
3 |
|
|
|
|
|
|
|
|||
критерий Гурвица можно записать в виде: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
a0 > 0; a1 > 0; a2 > 0; a3 > 0; |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
a1a2 − a0a3 > 0. |
|
|
|
|
|
|
|
||||||||
|
|
Для уравнения четвертой степени |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a |
|
d 4 y |
+ a |
d 3 y |
+ a |
|
d 2 y |
+ a |
dy |
+ a |
|
y = b |
d 4u |
+ b |
d 3u |
+ b |
d 2u |
+ b |
du |
+ b u |
|||||
|
4 |
dt4 |
3 |
dt3 |
|
2 |
dt2 |
1 |
dt |
|
|
0 |
|
|
4 |
dt4 |
3 |
dt3 |
2 |
dt2 |
1 |
dt |
0 |
||
критерий Гурвица имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
a0 > 0; a1 > 0; a2 > 0; a3 > 0; a4 > 0; |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
a a |
a |
3 |
− a2a |
4 |
− a |
a2 |
> 0. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
1 |
|
0 |
3 |
|
|
|
|
|
|
|
|||
6.3.Определение вида переходного процесса
всистеме третьего порядка
Если система описывается уравнением третьего порядка и в правой части отсутствуют члены с производными от входной величины
a |
d 3 y |
+ a |
d 2 y |
+ a |
dy |
+ a y = b u , |
(1) |
|
3 |
dt3 |
|
2 dt2 |
1 |
dt |
0 |
0 |
|
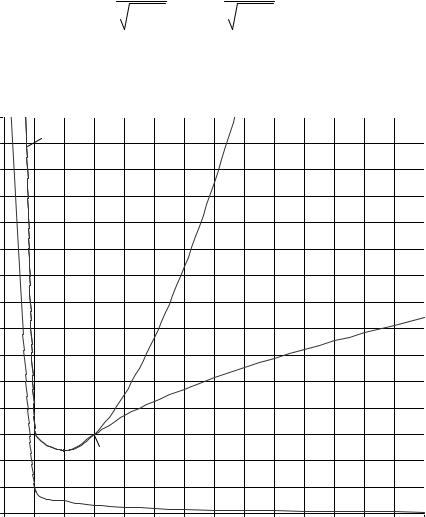
то по параметрам A и B с помощью диаграммы Вышнеградского (рис. 4) можно |
||||||||||||||||||
определить вид переходного процесса и выполнить проверку системы на ус- |
||||||||||||||||||
тойчивость. Параметры A и B определяют по коэффициентам правой части |
||||||||||||||||||
уравнения (1) согласно соотношений |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
A = |
a2 |
|
; |
B = |
a1 |
|
|
|
|
|
|
(2) |
||
|
|
|
|
|
3 |
a |
a2 |
|
|
3 a2a |
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
3 |
|
|
0 |
3 |
|
|
|
|
|
|
15B |
|
d |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
14 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13 |
|
|
|
|
O-2 |
|
|
|
|
|
|
|
O-1 |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
O-3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O-4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
0,05 |
1 |
2 |
3 |
4 |
|
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
||
Рис. 4. Диаграмма Вышнеградского
Линии a-b, c-d, c-f, c-e разграничивают на диаграмме четыре области: О-1, О-2, О-3, О-4. Первые три области соответствуют устойчивым переходным процессам, а четвертая область соответствует неустойчивым переходным про- цессам. При входном воздействии в виде единичной ступенчатой функции об- ласти О-1 соответствуют апериодические переходные процессы, области О-2 –

монотонные переходные процессы, области О-3 – колебательные переходные процессы.
Таким образом для определения вида переходного процесса или проверки системы на устойчивость по соотношениям (2) определяют параметры A и B, которые являются координатами, определяющими положение точки на диа- грамме Вешнеградского в той или иной области.
Границы областей описываются уравнениями:
AB =1, |
линия a-b; |
2A3 − 9AB + 27 = 0 (при A<3), |
линия c-d; |
A = (1+ 2α3 ) α2 , B = (α3 + 2) α (при α > 0), |
линии c-f и c-e. |
ВАРИАНТЫ ЗАДАНИЙ
7.ГИДРОМЕХАНИЧЕСКИЙ ПРИВОД
СДРОССЕЛЬНЫМ РЕГУЛИРОВАНИЕМ
Вгидроприводах с дроссельным регулированием используются гидро- двигатели с линейным перемещением выходного звена, гидродвигатели с не- полноповоротным вращением выходного звена и гидродвигатели с неограни- ченным вращательным движением выходного звена. Наиболее широкое рас-
пространение получили гидроприводы с линейным перемещением выходного звена. Управление распределительными устройствами гидромеханических при- водов осуществляется посредством рычажных механизмов.
Любой привод при работе должен преодолевать те нагрузки (силы и мо- менты сил), которые действуют на его выходное звено со стороны управляемо- го объекта. При расчетах приводов следует учитывать инерционную и позици- онную нагрузки, а также силы трения. Инерционная нагрузка создается масса- ми перемещаемых с ускорением частей управляемого объекта и выходного зве- на. Массы перемещаемых приводом частей при исследовании его динамики обычно заменяют приведенной к направлению движения выходного звена мас- сой.
Позиционная нагрузка характеризуется зависимостью преодолеваемых приводом усилий от перемещения выходного звена. Позиционную нагрузку оп-
ределять по линейной зависимости от положения выходного звена
F = cн yшт ,
где cн - коэффициент нагрузки; yшт - перемещение штока.
Силы трения, нагружающие выходное звено привода, возникают при движении частей управляемого объекта в окружающей среде, а также вследст-
вие трения в элементах соединения выходного звена с управляемым объектом и
вследствие трения в исполнительном гидродвигателе. Силу трения определять
по формуле
Fт р = kт р dyшт , dt
где kтр - коэффициент трения.
7.1.Гидромеханический привод с дроссельным регулированием
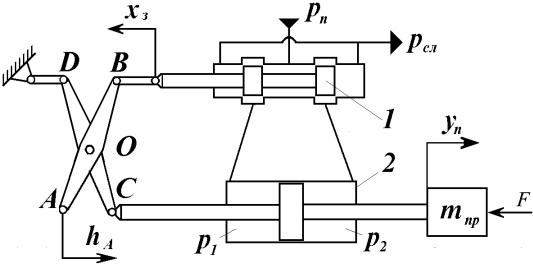
На рис. 7.1 дана схема следящего гидромеханического привода с дрос- сельным регулированием. Механизм управления гидроприводом состоит из рычагов AOB и COD. При смещении точки A рычага AOB в направлении, по- казанном на схеме стрелкой, золотник 1 смещается влево, соединяя левую по- лость гидроцилиндра 2 с напорной линией, а правую полость гидроцилиндра - со сливной линией. Под действием возникшего в полостях перепада давления поршень гидроцилиндра перемещается вправо. При этом точка C рычага COD, связанная со штоком, также перемещается вправо.
Рис. 7.1. Схема следящего гидромеханического привода с дроссельным
регулированием
Поршень гидроцилиндра будет перемещаться до тех пор, пока точка O не займет положения O′ , которому при фиксированном положении A′ точки A соответствует нейтральное положение золотника. Таким образом, перемещени- ем точки A рычага AOB осуществляется входное воздействие на данный сле- дящий привод, а рычагом COD обеспечивается отрицательная обратная связь от выходного звена (штока гидроцилиндра) к золотнику. За выходную (регули- руемую) величину принять перемещение штока. Коэффициенты передачи ме- ханизма управления зависят от отношения плеч рычагов AOB и COD.
Масса, приводимая в движение и приведенная к направлению движения штока гидроцилиндра обозначена m.
Значение параметров для различных вариантов приведены в таблице 7.1.
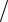
Таблица 7.1
ПАРАМЕТРЫ |
|
|
ВАРИАНТ |
|
|
||
|
|
1 |
2 |
3 |
|
4 |
5 |
Приведенная масса с учетом масс поршня |
400 |
500 |
600 |
|
700 |
800 |
|
и штока m, кг |
|
|
|
|
|
|
|
Диаметр поршня Dп , м |
|
0,1 |
0,12 |
0,14 |
|
0,16 |
0,2 |
Ход поршня lх , м |
|
0,5 |
0,6 |
0,7 |
|
0,8 |
0,9 |
Диаметр штока dшт , мм |
|
50 |
60 |
70 |
|
80 |
90 |
Диаметр золотника dз , мм |
|
25 |
32 |
20 |
|
32 |
25 |
Коэффициент расхода окон распределителя |
0,6 |
0,62 |
0,64 |
|
0,65 |
0,63 |
|
μз |
|
|
|
|
|
|
|
Коэффициент использования |
периметра |
0,7 |
0,8 |
0,9 |
|
1 |
0,85 |
золотника K п |
|
|
|
|
|
|
|
Плотность жидкости ρ, кг м3 |
|
840 |
850 |
860 |
|
870 |
880 |
Модуль объемной упругости |
жидкости |
1,2 |
1,3 |
1,4 |
|
1,3 |
1,2 |
Bж ×10−9 , Па |
|
|
|
|
|
|
|
Коэффициент нагрузки cн ×10−3 , н/м |
10 |
12 |
14 |
|
16 |
20 |
|
Коэффициент трения Kт р , н/(м/с) |
2 |
4 |
6 |
|
8 |
10 |
|
Давление питания pп , МПа |
|
10 |
12 |
14 |
|
16 |
20 |
Давление в сливной магистрали pс , МПа |
0,1 |
0,15 |
0,2 |
|
0,24 |
0,3 |
|
Коэффициент передачи механизма управ- |
1 |
1,2 |
1,4 |
|
1,6 |
1,8 |
|
ления K x h |
|
|
|
|
|
|
|
Коэффициент обратной связи Kо.с |
1 |
1,2 |
1,4 |
|
1,6 |
2 |
|
7.2. Гидромеханический привод с корректирующим устройством
Для обеспечения устойчивости гидропривода при высоком быстродейст- вии, при наличии большой приведенной к штоку массы и малых значениях ко- эффициента относительного демпфирования, приходиться применять коррек- тирующие устройства. Схема гидропривода с корректирующем устройством в виде канала 3 с малым проходным сечением (перетечки), соединяющем полос- ти гидроцилиндра приведена на рис. 7.2. Принцип действия данного гидропри- вода аналогичен работе гидропривода, описанного в п.7.1.
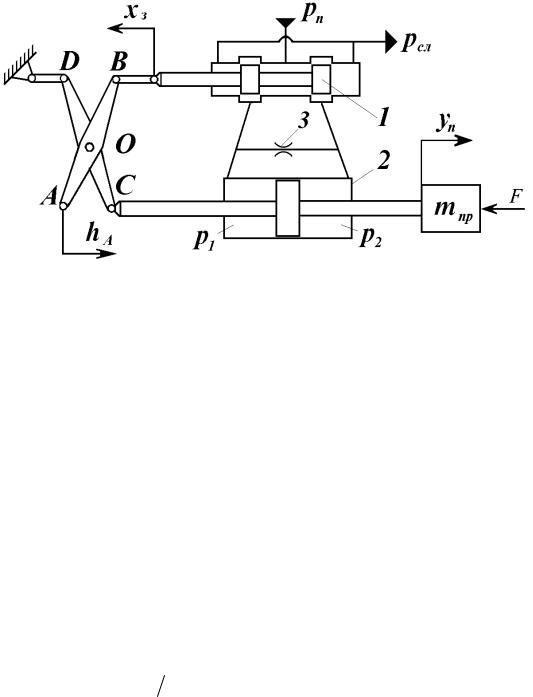
Рис. 7.2. Схема гидропривода с перетечками жидкости между полостями
гидроцилиндра
Значение параметров для различных вариантов приведены в таблице 7.2.
Таблица 7.2
ПАРАМЕТРЫ |
|
|
ВАРИАНТ |
|
|
||
|
|
1 |
2 |
3 |
|
4 |
5 |
Приведенная масса с учетом масс поршня |
400 |
500 |
600 |
|
700 |
800 |
|
и штока m, кг |
|
|
|
|
|
|
|
Диаметр поршня Dп , м |
|
0,1 |
0,12 |
0,14 |
|
0,16 |
0,2 |
Ход поршня lх , м |
|
0,5 |
0,6 |
0,7 |
|
0,8 |
0,9 |
Диаметр штока dшт , мм |
|
50 |
60 |
70 |
|
80 |
90 |
Диаметр золотника dз , мм |
|
25 |
32 |
20 |
|
32 |
25 |
Коэффициент расхода окон распределителя |
0,6 |
0,62 |
0,64 |
|
0,65 |
0,63 |
|
μз |
|
|
|
|
|
|
|
Коэффициент использования |
периметра |
0,7 |
0,8 |
0,9 |
|
1 |
0,85 |
золотника K п |
|
|
|
|
|
|
|
Плотность жидкости ρ, кг м3 |
|
840 |
850 |
860 |
|
870 |
880 |
Модуль объемной упругости |
жидкости |
1,2 |
1,3 |
1,4 |
|
1,3 |
1,2 |
Bж ×10−9 , Па |
|
|
|
|
|
|
|
Коэффициент нагрузки cн ×10−3 , н/м |
10 |
12 |
14 |
|
16 |
20 |
|
Коэффициент трения Kт р , н/(м/с) |
2 |
4 |
6 |
|
8 |
10 |
|
Давление питания pп , МПа |
|
10 |
12 |
14 |
|
16 |
20 |
Давление в сливной магистрали pс , МПа |
0,1 |
0,15 |
0,2 |
|
0,24 |
0,3 |
|
Коэффициент передачи механизма управ- |
1 |
1,2 |
1,4 |
|
1,6 |
1,8 |
|
ления K x h |
|
|
|
|
|
Коэффициент обратной связи Kо.с |
1 |
1,2 |
1,4 |
1,6 |
2 |
Коэффициент кинематической вязкости |
1 |
2 |
2,5 |
1,5 |
3 |
n ×104, м2 с |
|
|
|
|
|
Диаметр канала перетечки dк , мм |
2 |
2,5 |
3 |
2,5 |
2 |
Длина канала перетечки lк , мм |
20 |
25 |
30 |
25 |
20 |
7.3. Гидромеханический привод с демпфером
Для обеспечения устойчивости гидропривода при высоком быстродейст- вии, при наличии большой приведенной к штоку массы и малых значениях ко- эффициента относительного демпфирования, приходиться применять коррек- тирующие устройства. Схема гидропривода с корректирующем устройством в виде демпфера, подключенного к золотнику, приведена на рис. 7.3.
Рис. 7.3. Схема гидропривода с демпфером, подключенным к золотнику
Демпфер состоит из поршня 1, жестко соединенного с золотником. По- лости цилиндра 2 демпфера заполнены жидкостью. Полости цилиндра 2 соеди- нены между собой каналом с дросселем 3, по которому жидкость при движении поршня вместе с золотником перетекает из одной полости в другую. При этом возникает перепад давления, нагружающий золотник в осевом направлении си- лой, пропорциональной скорости движения поршня демпфера. Для того чтобы демпфер оказывал влияние на устойчивость гидропривода, точка А рычага АОВ должна перемещаться посредством упругого звена (т.е. пружины), жесткость которого обозначена ch . Принцип действия данного гидропривода аналогичен
работе гидропривода, описанного в п.7.1.
Значения параметров для различных вариантов приведены в таблице 7.3.

Таблица 7.3
|
|
ПАРАМЕТРЫ |
|
|
ВАРИАНТ |
|
|
||
|
|
|
|
1 |
2 |
3 |
|
4 |
5 |
Приведенная масса с учетом масс поршня |
400 |
500 |
600 |
|
700 |
800 |
|||
и штока m, кг |
|
|
|
|
|
|
|
|
|
Диаметр поршня Dп , м |
|
0,1 |
0,12 |
0,14 |
|
0,16 |
0,2 |
||
Ход поршня lх , м |
|
0,5 |
0,6 |
0,7 |
|
0,8 |
0,9 |
||
Диаметр штока dшт , мм |
|
50 |
60 |
70 |
|
80 |
90 |
||
Диаметр золотника, Dз , мм |
|
25 |
32 |
20 |
|
32 |
25 |
||
Диаметр штока золотника dшт.з , мм |
16 |
25 |
14 |
|
25 |
16 |
|||
Диаметр поршня демпфера DД , мм |
25 |
32 |
20 |
|
32 |
25 |
|||
Коэффициент расхода окон распределителя |
0,6 |
0,62 |
0,64 |
|
0,65 |
0,63 |
|||
μз |
|
|
|
|
|
|
|
|
|
Коэффициент |
использования |
периметра |
0,7 |
0,8 |
0,9 |
|
1 |
0,85 |
|
золотника K п |
|
|
|
|
|
|
|
|
|
Плотность жидкости ρ, кг м3 |
|
840 |
850 |
860 |
|
870 |
880 |
||
Модуль |
объемной упругости |
жидкости |
1,2 |
1,3 |
1,4 |
|
1,3 |
1,2 |
|
Bж ×10−9 , Па |
|
|
|
|
|
|
|
|
|
Коэффициент нагрузки cн ×10−3 , н/м |
10 |
12 |
14 |
|
16 |
20 |
|||
Коэффициент трения Kт р , н/(м/с) |
2 |
4 |
6 |
|
8 |
10 |
|||
Давление питания pп , МПа |
|
10 |
12 |
14 |
|
16 |
20 |
||
Давление в сливной магистрали pс , МПа |
0,1 |
0,15 |
0,2 |
|
0,24 |
0,3 |
|||
Коэффициент передачи механизма управ- |
1 |
1,2 |
1,4 |
|
1,6 |
1,8 |
|||
ления K x h |
|
|
|
|
|
|
|
|
|
Коэффициент обратной связи Kо.с |
1 |
1,2 |
1,4 |
|
1,6 |
2 |
|||
Коэффициент |
жесткости |
пружины |
30 |
35 |
40 |
|
45 |
50 |
|
ch ×10−4 , н м |
|
|
|
|
|
|
|
|
|
Коэффициент |
кинематической |
вязкости |
1 |
2 |
2,5 |
|
1,5 |
3 |
|
n ×104, м2 |
с |
|
|
|
|
|
|
|
|
Диаметр канала дросселя dк , мм |
|
2 |
2,5 |
3 |
|
2,5 |
2 |
||
Длина канала дросселя lк , мм |
|
20 |
25 |
30 |
|
25 |
20 |
||
