Пример 2. Вычисление производной.

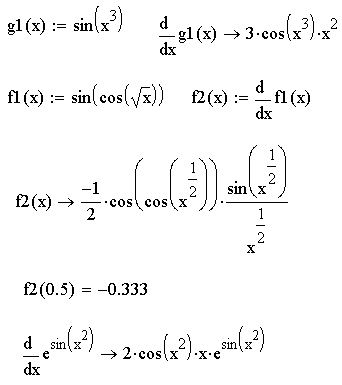
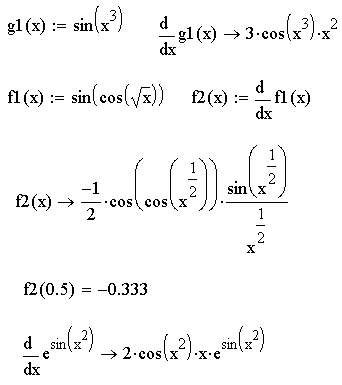
Рис. 2

Пример 3. Вычисление интеграла.

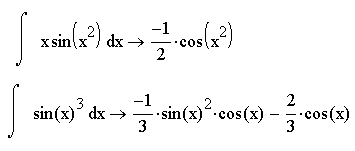
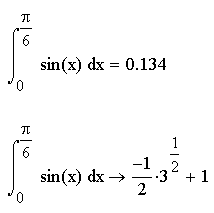
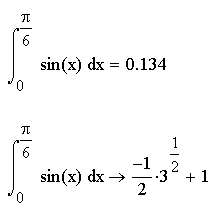
Рис. 3

№15. Решение задач линейной алгебры.

ЗАДАНИЕ. Решить систему уравнений 1) методом обратной матрицы и по правилам Крамера, сделать проверку. Систему уравнений 2) решить с помощью функции lsolve и решающего блока. Варианты заданий см. в работе №2.

Пример 4. Решить систему линейных уравнений при помощи правила Крамера:

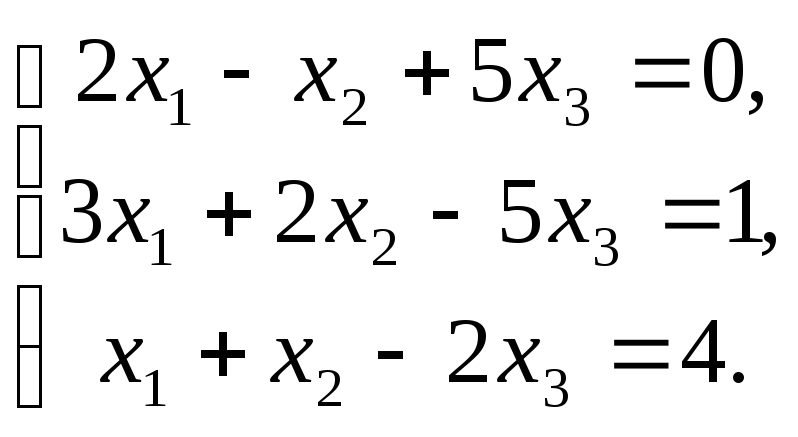
На рис. 4 приведен фрагмент рабочего документа, содержащий решение поставленной задачи.

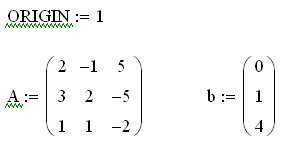
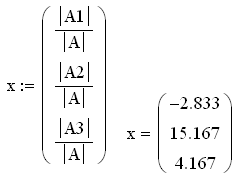
Рис. 4.

Пример 5. Решить систему линейных уравнений из примера 4 методом обратной матрицы. Решение показано на рис. 5.

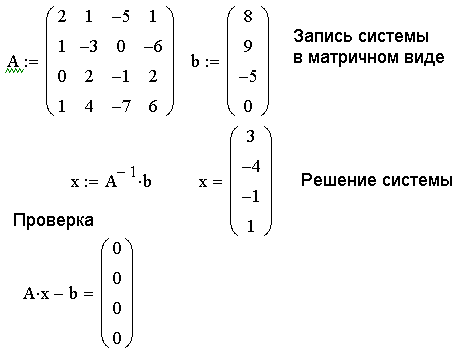
Рис. 5.

Пример 6. Решить систему с помощью функции lsolve и при помощи решающего блока:

x₁+2x₂+5x₃=-9, x₁–x₂+3x₃=2, 3x₁–6x₂–x₃=25.

Решение системы при помощи функции lsolve показано на рис. 6. Фрагмент рабочего документа на рис. 7 содержит пример применения решающего блока для решения системы.

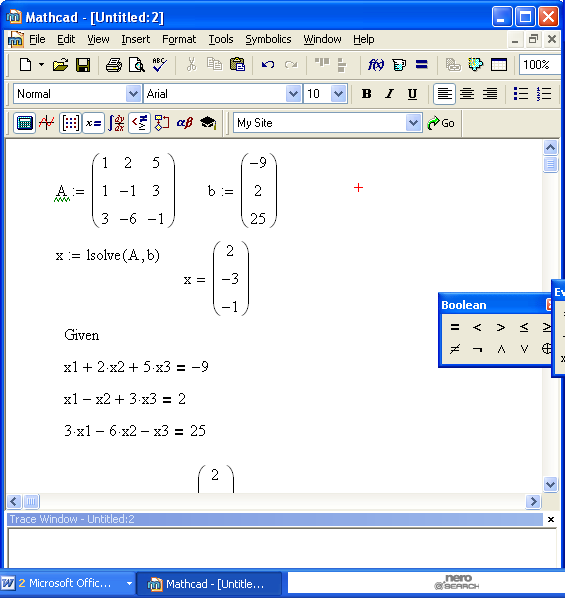
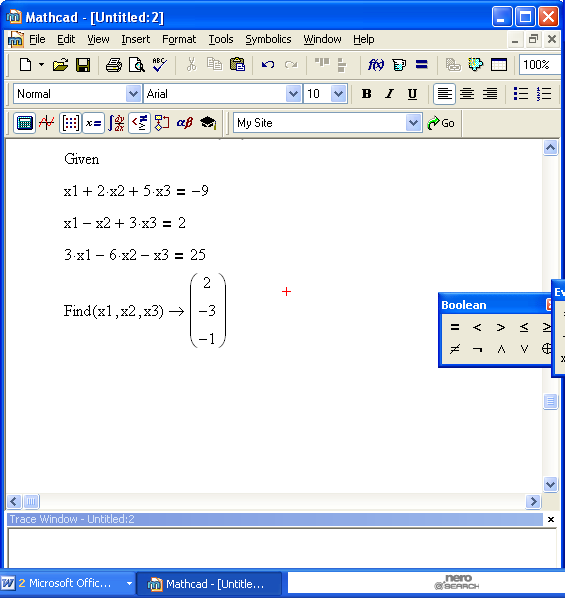
Рис. 6 Рис. 7

№16. Построение графиков на плоскости. Задание. Построить графики функции f(X). Варианты заданий см. № 3.

Пример 7. Построить график функции y=x\(x²–9). На рис. 8 изображен график заданной функции, которая терпит разрыв в точках 3 и –3.

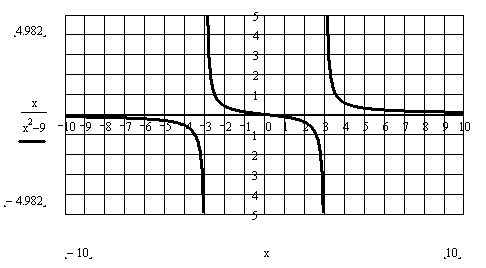
Рис. 8

Пример 8. Построить график функции заданной неявно: 5x²+3y²–15=0.

Приведем уравнение к каноническому виду: x²/3+y²/5=1. Разрешим уравнение относительно переменной у. Найдем область определения функции. Зададим ранжированную перемену и определим функции, описывающие верхнюю и нижнюю части эллипса. Построим график двух функций. Результат построения приведен на рис. 9.

Рис. 9

№17. Решение нелинейных уравнений и систем. Задание. Решить нелинейные уравнения и системы Варианты заданий см. В работе № 4.

Пример 9. Найти корни полинома 2x⁴–8x³+8x²–1=0.

Воспользуемся функцией polyroots(v), которая возвращает вектор всех корней (как вещественных, так и комплексных) полинома n–й степени, коэффициенты которого хранятся в массиве v, длиной n+1.

В нашем случае массив v следует определить как вектор столбец из пяти элементов¹(рис. 10). Решим задачу, так как показано на рис. 11. Найдем графическое решение заданного уравнения. Для этого создадим функцию F(x), определив полином как сумму произведений коэффициентов на x в соответствующей степени, и построим ее график. Точки пересечения графика с осью абсцисс и будут корнями уравнения. На рис. 12 видно, что графическое решение совпадает с аналитическим.

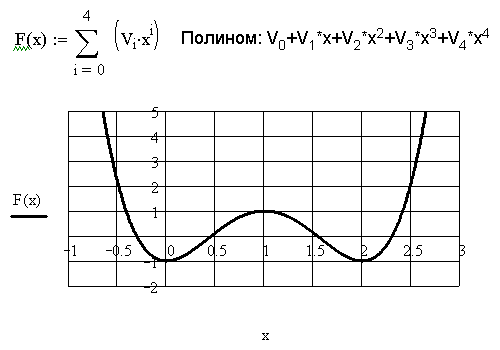
Рис. 10 Рис. 11 Рис. 12

Пример 15. Найти корни уравнения f(x)=0.

На рис. 13 видно, что график функции f(x) трижды пересекает ось абсцисс, то есть уравнение имеет три корня. Для решения этой задачи воспользуемся функцией root(F(x), x, a, b). Она возвращает с заданной точностью значение переменной x, при котором выражение F(x) равно нулю, a и b – пределы интервала изоляции корня. Понятно, что при такой форме записи функции нет необходимости задавать начальное значение x, так как оно определено в интервале [a,b]².

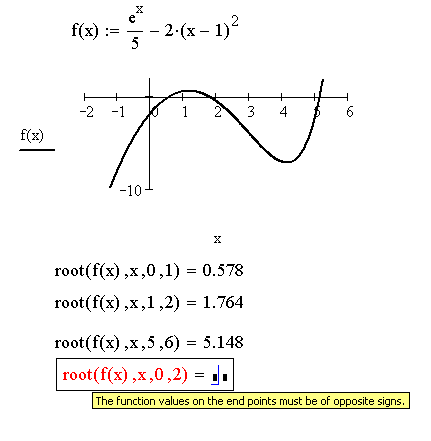
Рис.13

Пример 16. Решить систему уравнений: {x²+y²+3x–2y=4, x+2y=5}.

Данная система легко сводится к одному уравнению при помощи элементарных преобразований (рис. 14). Линейное уравнение решается относительно одного из двух неизвестных, например, можно выразить х через у, выполнив команду Symbolic\Variable\Solve при выделенном х. Полученное выражение необходимо подставить в квадратное уравнение и упростить(Symbolic\Variable\Collect).

Решение квадратного уравнения с одним неизвестным, полученного в результате преобразований заданной системы, приведено на рис. 15. Графическое решение уравнение показало, что имеется два действительных корня. Поэтому решающий блок используется дважды с соответствующими начальными значениями.

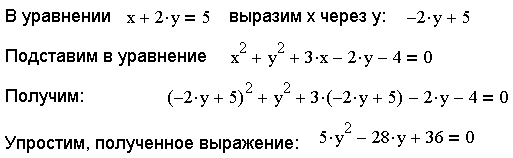
Рис. 14.

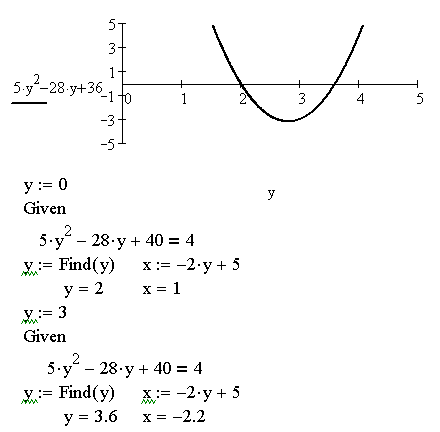
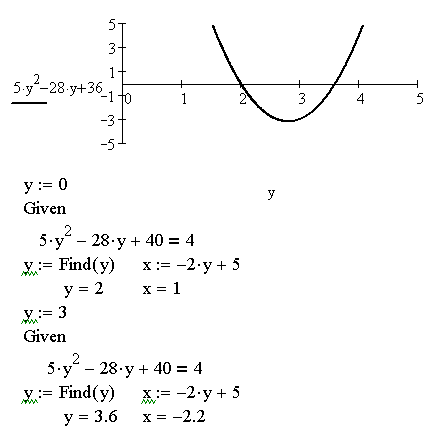
Рис. 15

На рис.16 показано, как решить систему с помощью решающего блока.

Рис. 16

1 Обратите внимание, что в уравнении отсутствует переменная x в первой степени. Это означает, что соответствующий коэффициент равен нулю.

2 Обратите внимание на последнее обращение к функции root на рис.3.78. MathCAD выдал сообщение об ошибке: «Значения на обоих концах интервала должны иметь противоположные знаки». Произошло это потому, что интервал изоляции задан неверно. На графике видно, что на концах этого интервала функция знак не меняет.

43