7.1.2. Структурная схема данной автоматической системы регулирования

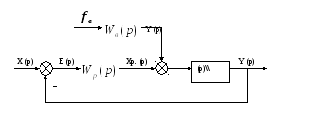
Рис. 7.3.

-передаточная функция объекта

- передаточная функция канала возмущающего воздействия

-передаточная функция канала регулирующего воздействия (для ПИД-регулирования, а для П -, И- и ПИ- регулирования –частные случаи из этого выражения).

7.2. Определение параметров передаточной функции объекта регулирования по экспериментальной переходной функции методом “площадей”

Построение математической модели линейной системы по экспериментальной переходной функции производится в следующем порядке:

• На основании формы переходной функции и в зависимости от физических свойств исследуемой системы устанавливается вид передаточной функции модели;

• Определяются значения коэффициентов передаточной функции из условия наилучшего приближения модели и объекта;

• Производится оценка точности аппроксимации:

Рассмотрим метод площадей:

Рассмотрим функцию h(t), которая получена из экспериментальной переходной функции объекта путем исключения чистого запаздывания  и нормировки. Пусть h(0)=h’(0)=0.

При аппроксимации функции h(t) на практике обычно задаются следующими структурами передаточной ф. модели:

(1.1)

(1.2)

(1.3)

В

ыражение:

обратное передаточной функции можно разложить в ряд по степеням p:

(1.4)

Очевидно, что для модели 1.1: a₁=S₁; a₂=S₂; a₃=S₃;

для модели 1.2: a₁=S₁; a₂=S₂; a₃=S₃;

для модели 1.3: коэффициенты b₁ , a₁ , … ,b_i , a_i где i=1,2,3 связаны с коэффициентами S_i разложения 1.4 системой уравнений:

a1=b1+S1 ;	a3=b1S2+S3 ;
	(1.5)
a2=b1S1+S2 ;	0=b1S3+S4 ;

Для определения S_i воспользуемся связью между S и некоторыми функциями от (1-h). Величину L(1-h) можно представить так:

Отсюда:

и

ли

(1.6)

Разложим функцию e^-pt в ряд по степеням pt:

(1.7)

Подставив этот ряд в уравнение (1.6), получим с учетом формулы (1.4) выражение:

(1.8)

Из выражения (1.8) следует, что коэффициенты S_i связаны с переходной функцией h(t) соотношением:

М

оментомi-го порядка функции 1-h(t) называется несобственный интеграл вида:

(1.9)

тогда: S₁ = M₀ ;

S₂ = S₁ М₀ - M₁ = S₁² – M₁;

S₃ = S₂ М₀ – S₁ M₁ + (1/2)* M₂ ;

S₄ = S₃ М₀ - S₂ M₁ + (1/2)*S₁ M₂ – (1/6)*M₃ ;

Определив по графику h(t) значения M_i методом численного интегрирования и вычислив из соотношений величины “площадей” S_i , определяют значения коэффициентов передаточной функции.

Выбор вида передаточной функции модели производится из следующих соображений, если коэффициенты S₁ , S₂ , S₃ положительны, то в зависимости от вида функции h(t) задаются моделью (1.1) или (1.2), если хоть один из коэффициентов S₁ , S₂ , S₃ отрицателен, задаются моделью (1.3).

В соответствии с выше изложенной методикой определяем коэффициенты передаточной функции по программе 1 (KP1.PAS – далее KP1), выбрав шаг дискретизации t=1 и произведя нормировку в соответствии с формулой:

График экспериментальных значений (кривая разгона)

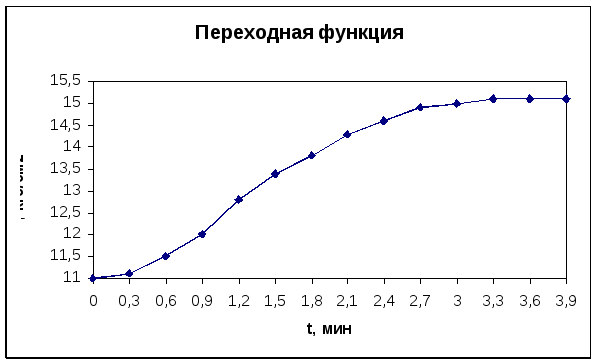
Рис. 7.4.

Приведение кривой разгона к нормированному, то есть безразмерному виду осуществляется с помощью формулы:

Таблица 7.2.

P, (нормирован-ные значения)	P1	P2	P3	P4	P5	P6	P7
	0	0,02439	0,121951	0,243902	0,439024	0,585366	0,682927
	P8	P9	P10	P11	P12	P13	P14
	0,804878	0,878049	0,95122	0,97561	1	1	1

Рис. 7.5.

(общий вид передаточной функции, так как коэффициенты положительны)

Используя программу кп-1 получаем следующие значения: