Основные элементы цепей.

1. Резистор.

Резистор-это элемент цепи, необратимо излучающий энергию в окружающее пространство.

Если его величина указанна и предполагается неизменной, то он линейный.

p(t)=u(t)ί(t) (теорема)

Указание u(t), ί(t) без указания их направления каким-либо способом лишено смысла и решением задачи не является!

2. Конденсатор.

Конденсатор принципиально отличается от резистора способностью запасать энергию.

,

3. Индуктивность. Запасает энергию.

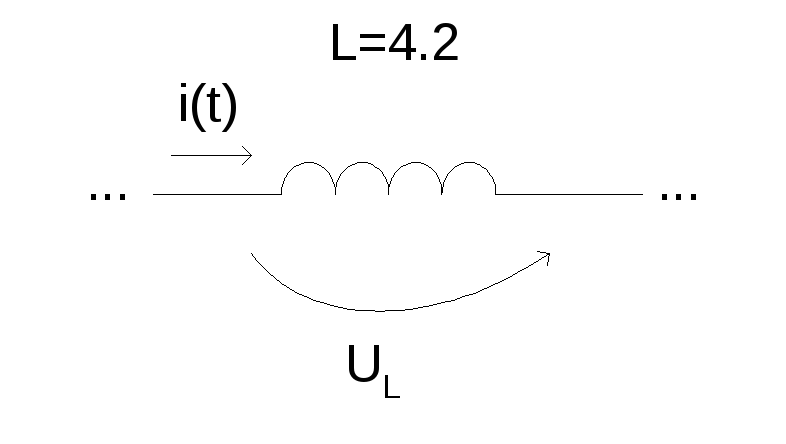
Цепь.

Цепью называется связанная совокупность элементов L,R,C предназначенная для целесообразного распределения элементов энергии.

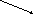Цепь.

Топология Параметры элементов

Топология может быть изложена в графовом, схемовом или матричном виде.

Параметры представляются в виде списка численных значений, если цепь линейна и в виде функциональной характеристики, если цепь не линейна.

Линейные цепи требуют составления системы линейных уравнений, которые можно записать в матрично-векторной форме и решать с помощью линейной алгебры.

Источники энергии.

Элементы R,L,C являются пассивными элементами. Их эксплуатация возможна только при наличии источников, преобразующих разные виды энергии в электрическую.

Сутью всякого такого преобразования является разделение зарядов с помощью сил не подчиняющихся закону Кулона - "сторонних сил".

Наиболее распространённым видом сторонних сил, в технике, являются электро-магнитные силы, использующие закон электромагнитной индукции.

ИИН:

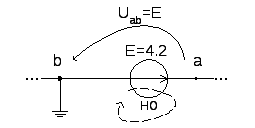
ИИТ:

u_ab=φ_a- φ_b=E

Идеальный источник, непрерывно поддерживающий на своих зажимах строго постоянную

разность потенциалов, не зависит от величины токов.

ИИТ поддерживает строго постоянный ток, не зависит от напряжении на нём.

Электрическая цепь представляемая элементами и соединяющими проводами, которые не имеют сопротивления в наших задачах.

Чего не нарисовано того нет!

Т.о. ТЭ оперирует с математическими моделями элементов и составлением из них цепей.

Основная задача анализа цепи это нахождение токов в её ветвях, при заданной топологии и параметров.

Указание решения задачи без указания направления токов недопустимо!!!

Перед началом решения основной задачи анализа необходимо, из соображений, задать направления токов всех ветвей.

В течение решения задачи направление токов не менять, иначе ответы утратят смысл.

При начале реализации методов решения произвольно назначаются направления токов, в ходе реализации решения являются законом для данной задачи!

В связи с произволом в первоначальном назначении токов существует правило оптимальных назначений - необязательное, соответствующее некоторым вычислительным удобствам - смотри ниже.

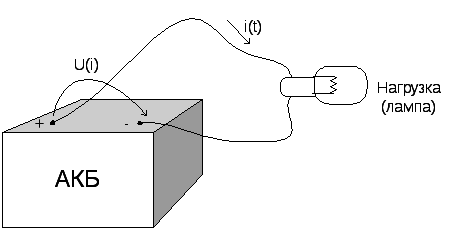
Для линейных расчётов удобно нелинейные характеристики источников заменять линейными, вводя вместо реальной u(ί) её материальную модель.

Линейная модель РИН оставляет уравнение цепи линейной и позволяет решать их с помощью методов линейной алгебры.

Параметры линейной модели любого реального источника можно выяснить физическим экспериментом. Наиболее наглядный эксперимент холостого хода и короткого замыкания, хотя математически они ничем не отличаются от любых других двух экспериментов. Поскольку линейная модель не отражает всей характеристики, то физический эксперимент по получению линейных параметров следует проводить при каких-либо полезных("рабочих") значениях токов.

Приведённой линейной модели соответствует точная линейная эл. цепь.

ίR_нагр.+ ίR=E

РИН отличается от ИИН величиной R_ί. У ИИН R_ί=0.

Оптимальная нагрузка РИН.

Меняя величину R_нагр., будем получать разные токи, соответственно будет меняться мощность.

P_нагр.=R_нагр.ί²=u_нагр.ί

R_нагр=R_оптим.

На холостом ходу мощность нагрузки равна нулю, так же, как и в режиме короткого замыкания.

Нетрудно показать, что мощность нагрузки максимальная при R_нагр.=R_ί

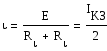
Если монотонно уменьшить величину внутреннего сопротивления у математической модели, то при неизменной величине E, величина оптимального тока будет расти. Этому соответствует увеличение оптимальной, т.е. максимальному извлеканию из источника мощности. При R_ί стремящееся к нулю, P_max стремящееся к бесконечности. Это означает что ИИН имеет бесконечно большую мощность. R_ί всегда имеет ограниченную мощность т.е. R_ί неравное нулю.

Реальный источник тока (РИН).

ИИТ есть абстрактная математическая модель, при рассмотрении физической стороны которой выясняется её неосуществимость.

ИИТ нельзя размыкать!

В действительности ИТ осуществляется в форме РИТ, у которого собственный ток может замыкаться через собственное сопротивление или через собственную внутреннюю проводимость.

R_внутр.=

Т.о. РИТ может приносить пользу, если его R_внутр есть конечная величина.

Исследование ВАХ РИТ --->u_нагр=f(ί_нагр)

ПЗК:

Графически характеристики РИН и РИТ идентичны, а при совпадении параметров

R_ί =E и R_ί=R_ί(*)

Т.о. если получается параметр математической модели источника в форме РИТ то от них можно перейти к параметрам эквивалентного РИН и наоборот, соблюдая условие (*)

В действительности располагая реальным источником сторонней силы мы можем для его представления в схеме использовать либо математическую модель в форме РИН, либо математическую модель в форме РИТ- в зависимости от удобств дальнейшего расчёта. Модель в форме РИТ удобна в формах с параллельными источниками, а РИН удобна при последовательном соединение источника. Определить по виду технически реального источника его близость к РИН или РИТ весьма трудно

Различие между РИН и РИТ при их формальной эквивалентности проявляется в крайних режимах:

1. на холостом ходу

2) при КЗ

Удобнее всего такую задачу решать с применением преобразования РИН в РИТ

Далее исследуем полученную цепь на величину предельной мощности и оцениваем целесообразность комбинирования источников.

Преобразование РИН в РИТ резко упрощает решение задачи.

Аналогичным образом РИН в РИТ может упрощать решение и более сложных задач.

Основные соотношения и законы для решения основных задач анализа цепей.

ОЗА- токи в ветвях.

ОЗА поставлена, если:

1) топология - схема, граф, матрица.

2) Параметры- список направление тока и направление

Ток через конденсатор при переменном напряжении является током смещения и никак не связан с не совершенствованием его изоляции.

S

Постулат Максвелла.

К конституционным законам относятся к энергетическим соотношениям.

Законы для цепи.

U_R=Rί- закон Ома.

ПЗК:

Алгебраическая сумма токов в узле равна нулю.

Принцип непрерывного тока, порождает ПЗК следует из закона полного тока в связи с тем что поток вектора ротора сквозь замкнутую поверхность всегда равно нулю.

Правило знаков для ПЗК можно связать с правилом знаков для ПНТ- тогда выход из узла токи считают со знаком (+).

Правило знаков для ПЗК может быть произведено, но оно должно быть.

Необходимо учитывать, то, что ПНТ справедлив для токов любой природы, включая токи смещения.

Закон ВЗК:

ВЗК справедлив только для мысленно замкнутого контура.

_abR+U_am=-E

𝝋_a- 𝝋_m=-E-i_abR

Полный замкнутый комплект уравнений для цепей постоянного тока.

узел-вершина

∑it = E

1. Нумеруем токи и назначаем направления

2. Число токов равно числу ветвей, то есть оно определяет порядок n системы линейных уравнений (n = 6)

ПЗК = q – 1 (число узлов без одного)

ПЗК = 3

ВЗК = n – (q – 1) (уравнений столько, сколько ветвей)

Задав направления токов в ветвях, мы ненаправленный граф цепи можем превратить в направленный орграф.

Неустранимым узлом цепи принято называть место соединения более, чем двух ветвей.

Устранимым узлом может быть любая точка схемы, кроме неустранимых.

Избрать независимые контуры для того, чтобы в них назначить направления обхода и составить уравнения ВЗК.

Число независимых контуров = ВЗК = n – (q – 1).

q = 4 I1 – I2 – I3 = 0 (n)

n = 6 I3 – I5 – I6 = 0 (m)

ПЗК = 3 I2 + I5 + I4 = 0 (b)

ВЗК = n – 3 = 3

I1R1 + I2R2 – I4R4 = E1 + E2 (НО1)

– I2R2 + I3R3 + I5R5 = – E2 – E3 (НО2)

I4R4 – I5R5 + I6R6 = – E4 (НО3)

Все пакеты для ПК системы линейных алгебраических уравнений (СЛАУ) воспринимают только в матрично-векторной форме.

Запишем в матрично-векторной форме:

I1 I2 I3 I4 I5 I6

1	-1	-1
		1		-1	-1
	1		1	1
R1	R2		-R4
	-R2	R3		R5
			R4	-R5	R6

[K] =

[K]^-1[K] Ī = [K]^-1Ē

Ī = [K]^-1Ē решение ОЗАЦ

Можно показать, что матрица связной цепи никогда не имеет определителя = 0. Она всегда неособенная.

Возможные алгоритмы решения уравнений цепи.

1. Простейшим методом является метод Гаусса (метод подстановок) требует n³ операций.

2. Метод определителей (метод Крамера) требует n! операций. Метод Крамера на практике не применять!

Матричная форма метода Гаусса.

Метод Гаусса предусматривает подстановки неизвестных в порядке возрастания их номеров. Этим подстановкам в цепях соответствуют преобразования цепей с упражнением токов в порядке их нумерации.

После первого шага метода Гаусса СЛАУ соответствует цепи, в которой нет тока I1, после второго – нет тока I2 и так далее. Именно поэтому имеет смысл пошаговое выполнение метода Гаусса вместо общей операции [K]^-1.

Для выполнения первого шага метода Гаусса необходимо исходную СЛАУ умножить на следующую матрицу:

1
	1
		1
-R1			1
				1
					1

1	-1	-1
		1		-1	-1
	1		1	1
R1	R2		-R4
	-R2	R3		R5
			R4	-R5	R6

I1

I2

I3

I4

I5

I6

=

N-матрица N1

1
	1
		1
-R1			1
				1
					1

0

0

0

E1+E2

– E2 – E3

– E4

=

N1

N-матрица состоит из единичной диагонали и одного ненулевого столбца ниже этой диагонали, имеющего i-ый номер на i-ом шаге метода Гаусса, исключающем i-ую неизвестную из СЛАУ.

Каждый элемент этого столбца N[i, j] состоит из

где, K – матрица Кирхгоффа после предыдущего (i – 1) шага метода Гаусса.

Целью N-1 шагов такого типа является превращение исходной матрицы Кирхгоффа в верхнетреугольную (т.е. имеющую нули ниже главной диагонали). В последней строке преобразованной СЛАУ находится скалярное уравнение, содержащее одну n-ую неизвестную. Выполнив (n – 1) шагов, получим в последней строке

8.2 I6 = 29 => I6

Матричная форма шагов метода Гаусса описывает все возможные эквивалентные преобразования цепей, поскольку при выполнении операций значение неизвестных (токов) не меняется, а остающийся квадратным фрагмент исходной матрицы соответствует всегда некоторой реализуемой цепи, то есть существует несколько путей.

Провести самостоятельно умножение на N2 (например, с помощью символьного пакета).

Анализируя последнюю строку после выполнения умножения на N1 и N2 легко убедиться, что она описывает цепь:

Таким образом, действительно последовательные умножения на N матрицы содержат в себе параллельно-последовательные преобразования, преобразования РИН-РИТ, преобразования звезда-треугольник.

Сама форма N-матрицы предельно проста, легко может быть описана программными средствами один раз на все необходимые шаги.