9. Построение лах и лфх скорректированной разомкнутой системы. Оценка запасов устойчивости скорректированной системы по модулю и по фазе.
Построим ЛАХ и ЛФХ скорректированной разомкнутой системы с помощью приложения Simulink пакета Matlab.
Рис. 11 - Структурная схема разомкнутой скорректированной системы.
Рис. 12 - ЛАХ и ЛФХ разомкнутой скорректированной системы
Запас устойчивости системы по модулю:
20lg L=-10.1; m=1-L =0.69;
Запас устойчивости системы по фазе: =180-117=63.
После введения корректирующего устройства система стала более устойчивей, что наглядно видно из ЛАХ и ЛФХ скорректированной разомкнутой системы по увеличению запасов устойчивости по модулю (m=0.69) и по фазе (=63).
10. График переходной функции скорректированной системы. Оценка показателей качества скорректированной системы
Построим график переходной функции h(t) скорректированной системы в приложении Simulink пакета Matlab.
Рис. 13 - Структурная схема замкнутой скорректированной системы
Рис. 14. Переходный процесс скорректированной системы
Определим показатели качества скорректированной системы:
Из рисунка 15 определяем перерегулирование системы:
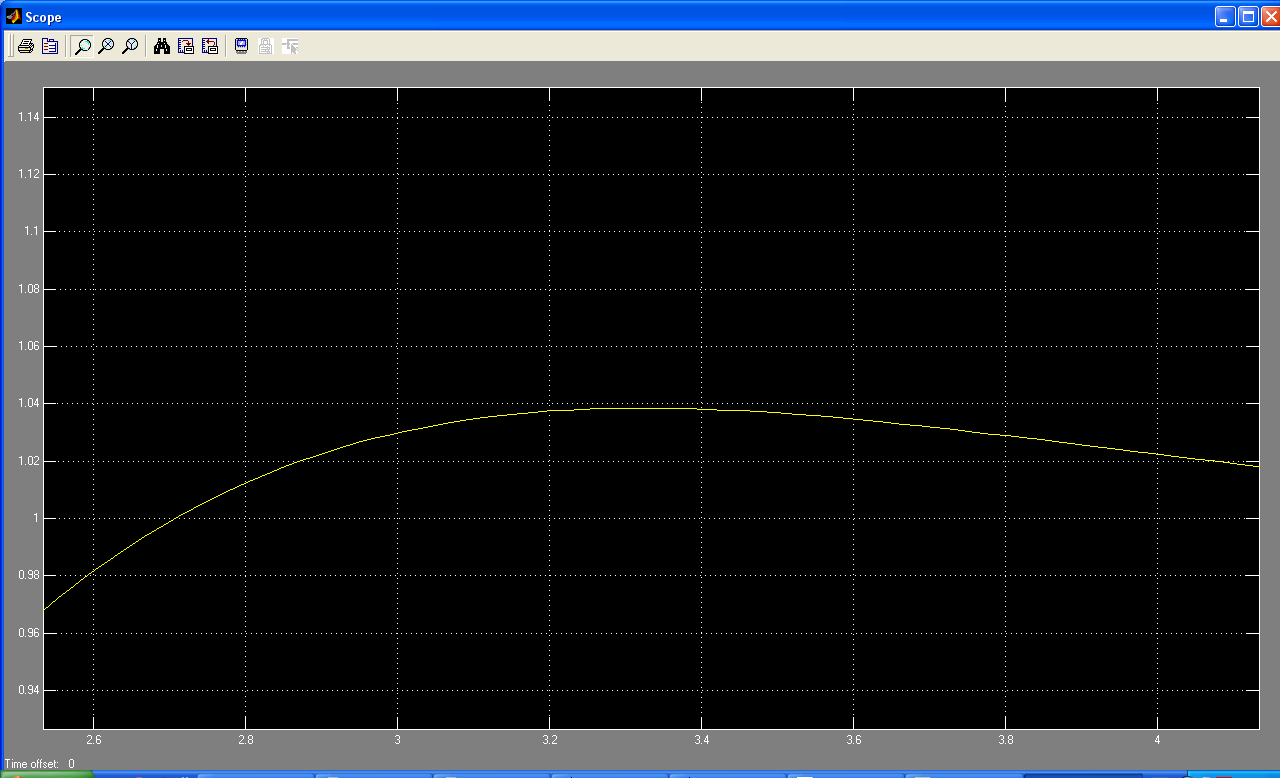
Рис. 15- Переходная характеристика замкнутой скорректированной системы в увеличенном масштабе
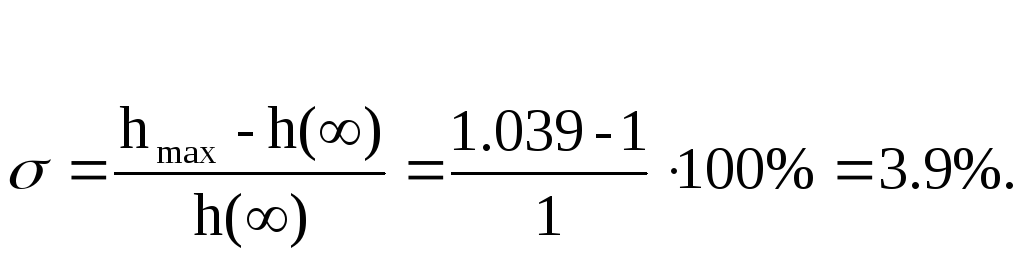
Исходя из рисунка 16 можем определить время регулирования системы:
Рис. 16 - Переходная характеристика замкнутой системы в увеличенном масштабе
После введения корректирующего устройства система стала более устойчивой. Полученные значения показателей качества скорректированной системы полностью удовлетворяют требуемым (tрег<=2.5; <=5%).
Таким образом, с помощью метода Соколова Н.И. было синтезировано последовательное корректирующее устройство, которое было введено в систему для достижения требуемых показателей качества. В результате была получена скорректированная система, полностью удовлетворяющая требуемым показателям качества: время регулирования равно 2.5 секунды и величина перерегулирования равна 3.9%.
Заключение
В результате выполнения данной курсовой работы была спроектирована и исследована система автоматического управления техническими объектами. Было проведено исследование динамических характеристик и синтез корректирующего устройства следящей системы для обеспечения показателей качества управления (заданных величин перерегулирования и времени регулирования) с использованием пакетов моделирования MatLab.
Система изначально оказалась устойчивой по алгебраическому (Гурвица) и по частотному (Михайлова) критериям.
Были построены частотные характеристики (АФХ, АЧХ, ФЧХ), а также логарифмические частотные характеристики (ЛАХ, ЛФХ), произведена оценка устойчивости САУ с помощью алгебраического и частотного критериев.
Определены запасы устойчивости системы по модулю и по фазе с помощью ЛАХ и ЛФХ.
Произведен синтез последовательного корректирующего устройства методом Соколова.
По графикам переходных характеристик определены показатели качества (время регулирования и перерегулирование) нескорректированной и скорректированной системы.