3. График переходной функции заданной нескорректированной системы. Оценка показателей качества нескорректированной системы

Переходная функция h(t) звена – это реакция звена на единичное воз - действие 1(t) при условии, что до момента приложения воздействия звено находилось в состоянии покоя, т.е. начальные условия были нулевыми.

Построим график переходной функции h(t) заданной нескорректированной системы в приложении Simulink пакета Matlab:

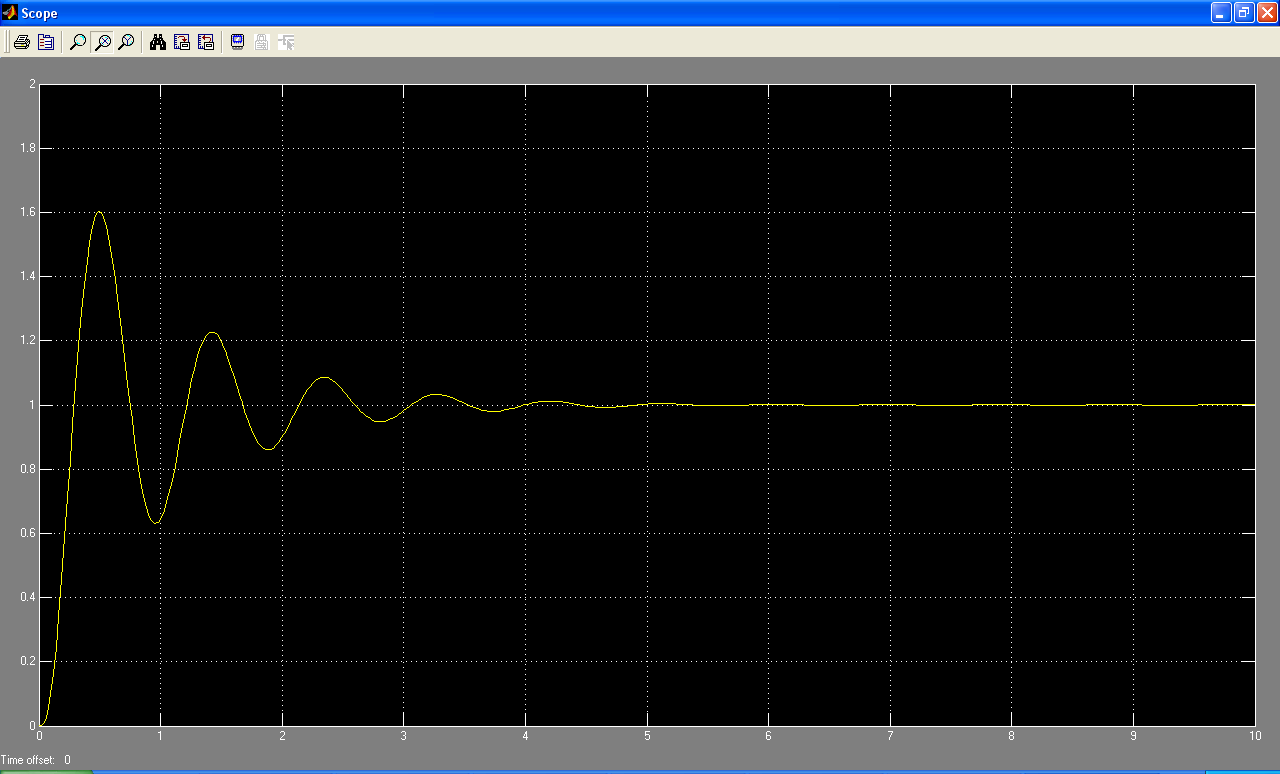
Рис. 9- Переходный процесс нескорректированной системы

Склонность системы к колебаниям, а, следовательно, и запас устойчивости могут быть охарактеризованы максимальным значением управляемой величины h_max или так называемым перерегулированием :

, где h()0 представляет собой установившееся значение управляемой величины после завершения переходного процесса.

Быстродействие системы определяется по длительности переходного процесса t_p. Длительность переходного процесса определяется как время, протекающее от момента приложения на вход единичного скачка до момента , после которого имеет место неравенство , где- заданная малая постоянная величина, представляющая собой обычно допустимую ошибку; под

обычно принимают некоторую долю входного воздействия, составляющую, как правило, от 1 до 5% величины скачка на входе.

Определим показатели качества нескорректированной системы:

Из рисунка 9 определяем перерегулирование системы:

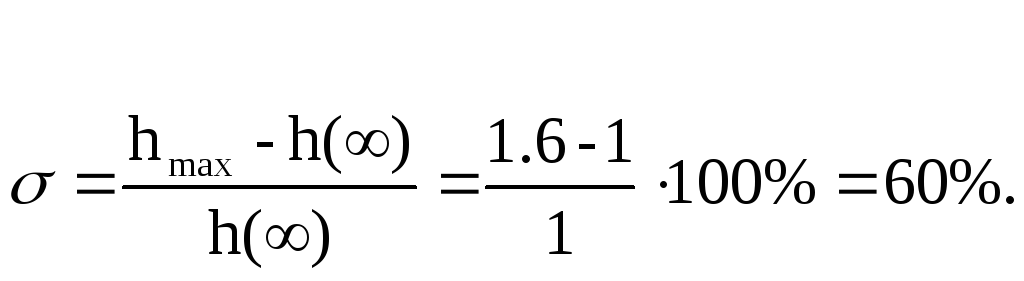
Исходя из рисунка 10 можем определить время регулирования системы:

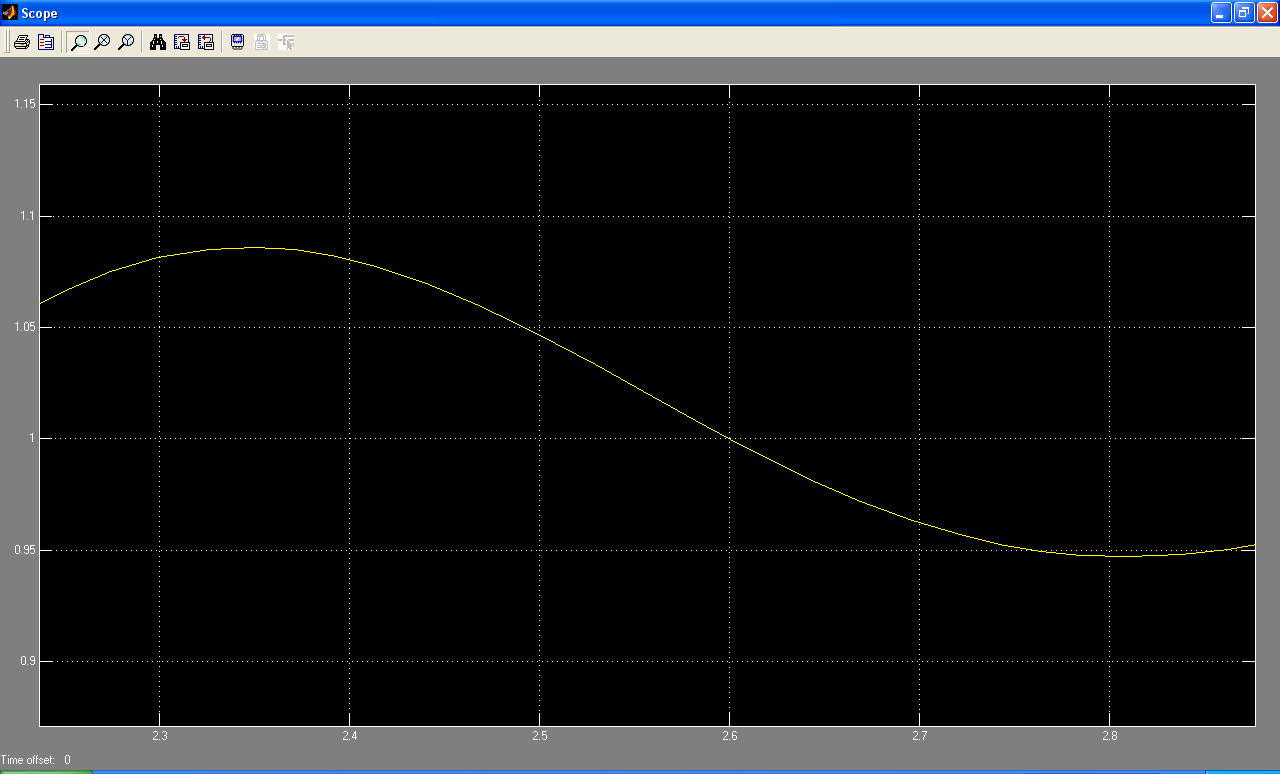
Рис. 10- Переходная характеристика замкнутой системы в увеличенном масштабе

Перерегулирование нескорректированной системы не удовлетворяет требуемому (<=5%), а время регулирования лежит в пределах требуемых значений (t_рег<=2.5).

8. Синтез последовательного корректирующего устройства методом Соколова.

Проведем синтез последовательного корректирующего устройства методом Соколова.

Передаточная функция нескорректированной системы:

1) Определяем разность порядков полиномов числителя (m₁) и знаменателя (n₁) передаточной функции замкнутой нескорректированной системы (n₁-m₁):

Формируем желаемую передаточную функцию замкнутой системы, на основе нормированных передаточных функций. Заданный порядок астатизма системы: ν_зад=1.

Нормированная функция имеет вид:

Определяем порядок числителя и знаменателя нормированной передаточной функции:

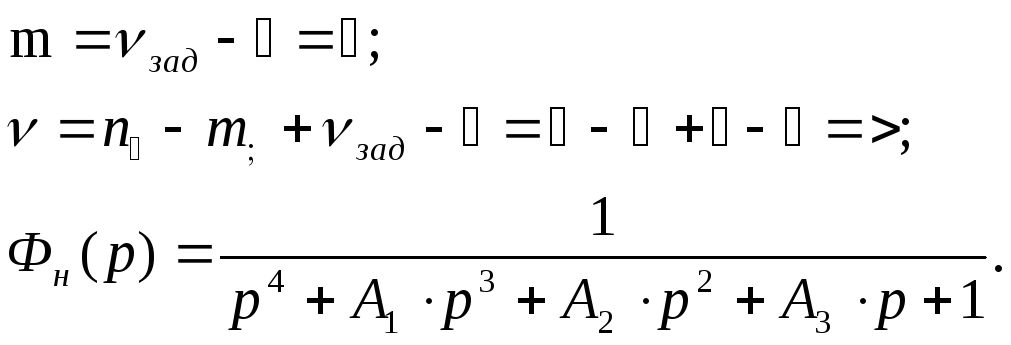
2) Коэффициенты нормированной передаточной функции для критического затухания переходного процесса выбираем исходя из показателей качества. Т.к. время регулирования t_рег укладывается в необходимые пределы, а требуемое перерегулирование (=5%) оказалось значительно меньше полученного(=60%), то воспользуемся приложением А, таблицей А.2, из которой определим значения коэффициентов, а также нормированное время: 1; 3; 4.25; 3; 1; τ_н=5.1.

Желаемая передаточная функция выбирается с использованием теоремы масштабов преобразования Лапласа:

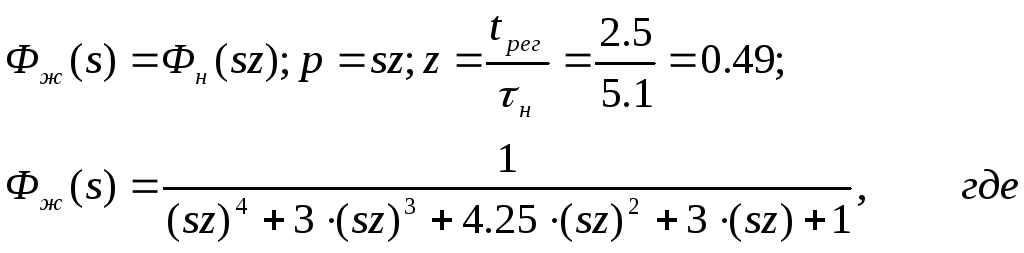
p – аргумент нормированной передаточной функции,

s – комплексный аргумент Лапласа,

z – коэффициент масштаба времени,

t_рег – заданное время регулирования,

–время регулирования нормированной передаточной функции.

Определяем желаемую передаточную функцию:

3) Определим корректирующее устройство: