1.1 Исследование заданной системы на устойчивость двумя критериями.
Под устойчивостью подразумевается способность системы возвращаться в исходное или близкое к нему состояние, после снятия внешнего воздействия с системы.
а). Критерий Гурвица.
Критерий Гурвица относится к алгебраическим критериям устойчивости. Алгебраические критерии устойчивости позволяют определить устойчивость системы по коэффициентам характеристического уравнения.
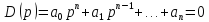
Для устойчивости линейной САУ необходимо и достаточно, чтобы определитель Гурвица и все его главные диагональные миноры были положительными.
Правило составления определителя Гурвица: по главной диагонали записывается в порядке возрастания индекса коэффициенты характеристического уравнения начиная с аь вниз от главной диагонали записываются коэффициенты с убывающим индексом, вверх с возрастающим, недостающие заполняются нулями.
Для определения характеристического уравнения нужно получить передаточную функцию замкнутой системы.
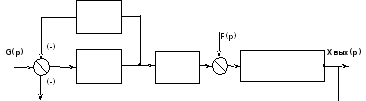
Сначала определим передаточную функцию разомкнутой системы. Для получения замкнутой функции по управляющему воздействию, возмущающее воздействие приравнивается к нулю (F(p)=0).
Для получения передаточной функции разомкнутой системы размыкается главная обратная связь и точка разрыва считается входом и выходом системы. Затем преобразуем структурную схему САУ. По правилу определения передаточной функции нескольких последовательно соединенных звеньев найдем результирующую передаточную функцию. Она равна произведению передаточных функций отдельных звеньев.
Тогда схема примет вид:
По правилу определения передаточной функции звеньев охваченных отрицательной обратной связью найдем результирующую передаточную функцию, затем по правилу определения передаточной функции нескольких последовательно соединенных звеньев найдем результирующую передаточную функцию. Она равна произведению передаточных функций отдельных звеньев.
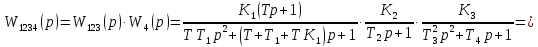
После преобразований у нас осталось одно звено с передаточной функцией
После подстановки значений коэффициентов получим
Теперь мы можем определить передаточную функцию по управляющему воздействию в замкнутом состоянии.
Восстановим главную обратную связь
и т.к. это единичная обратная связь, то для нахождения передаточной функции по управляющему воздействию в замкнутом состоянии воспользуемся формулой:
Допустим, что
следовательно
, тогда по аналогии
Получим
Запишем характеристическое уравнение САУ в замкнутом состоянии.
Для нахождения характеристического уравнения САУ в замкнутом состоянии приравняем
к нулю знаменатель передаточной функции замкнутой системы, получим
Зная характеристическое уравнение, мы можем составить Определитель Гурвица и его главные диагональные миноры.
Условия устойчивости Критерия Гурвица не выполняются (для устойчивости линейной САУ необходимо и достаточно, чтобы определитель Гурвица и все его главные диагональные миноры были положительными), следовательно, данная САУ является неустойчивой.
б). Критерий Найквиста (в логарифмических координатах).
Критерий Найквиста относится к частотным критериям устойчивости. Частотные критерии устойчивости позволяют судить об устойчивости САУ по виду их частотных характеристик.
Для определения устойчивости необходимо рассмотреть логарифмические
амплитудно-частотные характеристики. По их взаимному расположению судят об устойчивости замкнутой системы.
Сформулируем критерий Найквиста в логарифмических координатах. Если разомкнутая система устойчива, то для устойчивости заданной САУ необходимо и достаточно, чтобы ЛФЧХ при изменении частоты от 0 до ∞ пресекала линию 180 град справа от частоты среза (точка пересечения ЛАЧХ с осью абсцисс).
Преобразуем структурную схему САУ в одноконтурную, состоящую из последовательно соединённых типовых динамических звеньев. Часть преобразований мы проделали при нахождении передаточной функции.
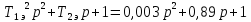
Т.к. коэффициент демпфирования больше 1, то колебательное звено нужно разложить на 2 апериодических звена.
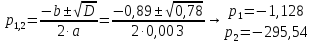
Преобразуем уравнение:
Структурная схема примет вид.
Значит второе колебательное звено не нужно раскладывать на два апериодических.
Таким образом, у нас получилась система состоящая из трёх апериодических, одного колебательного звена и одного форсирующего звена первого порядка. Значит ЛАЧХ будет иметь 5 изломов в точках:
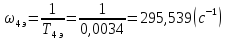
Рассчитаем
:
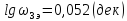
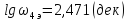
Полученные величины откладываем на соответствующих осях координат.
ЛАЧХ состоит из четырех участков:
участка с наклоном 0 дБ/дек
участка с наклоном 0 дБ/дек - 20дБ/дек = - 20дБ /дек
участка с наклоном - 20дБ /дек - 20дБ/дек = - 40 дБ/дек
участка с наклоном - 40 дБ/дек + 20дБ/дек = - 20 дБ/дек
участка с наклоном - 20 дБ/дек - 40дБ/дек = - 60 дБ/дек
участка с наклоном - 60 дБ/дек - 20дБ/дек = - 80 дБ/дек
Каждая асимптота проводиться до следующей по величине частоты сопряжения. Ее наклон изменяется на - 20 дБ/дек для апериодических звеньев, - 40 дБ/дек для колебательного звена и на +20 дБ/дек для форсирующего звена первого порядка.
Для построения ЛФЧХ по оси ординат откладывают величину фазы φ в градусах, а по оси абсцисс логарифм частоты в декадах. В этом случае фазовая характеристика звена определяется выражением:
Расчет произведем в программе MathCAD.
Если разомкнутая система устойчива, то для устойчивости заданной САУ необходимо и достаточно, чтобы ЛФЧХ при изменении частоты от 0 до да пресекала линию 180 град справа от частоты среза (точка пересечения ЛАЧХ с осью абсцисс). Это условие не выполняется, следовательно система неустойчива.
ЛФЧХ и ЛАЧХ изображены на рис. 1