5. Расчёт оптимальных параметров настройки регулятора
5.1. Расчёт параметров регулятора на основании интегральной квадратичной оценки
Передаточная функция ОУ:
(5.1.1)
Передаточная функция регулятора:
,
тогда передаточная функция всей системы
в разомкнутом состоянии будет:
(5.1.2)
Передаточная функция ошибки данной САУ:
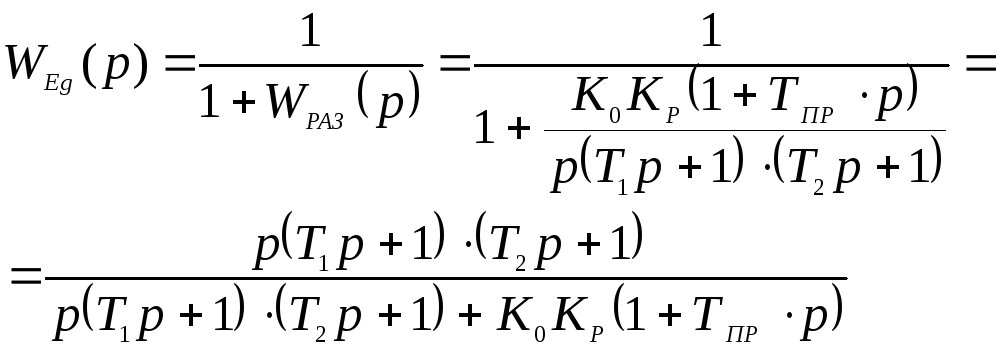(5.1.3)
Изображение
входного ступенчатого сигнала
,
тогда изображение ошибки:
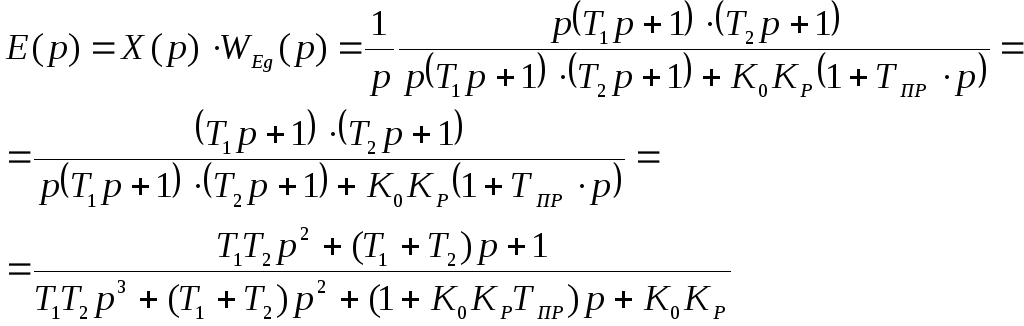(5.1.4)
Изображение ошибки представим в следующем виде:
,
где (5.1.5)
;
;
;
;
.
Теперь, для того чтобы вычислить квадратичную интегральную оценку можно воспользоваться табулированными значениями интегралов, приведёнными в литературе [7].
(5.1.6)
Для нахождения
параметров настройки регулятора (
,
),
при которых будет обеспечен минимум
квадратичной оценки, берём частные
производные по данным параметрам от
последнего выражения.
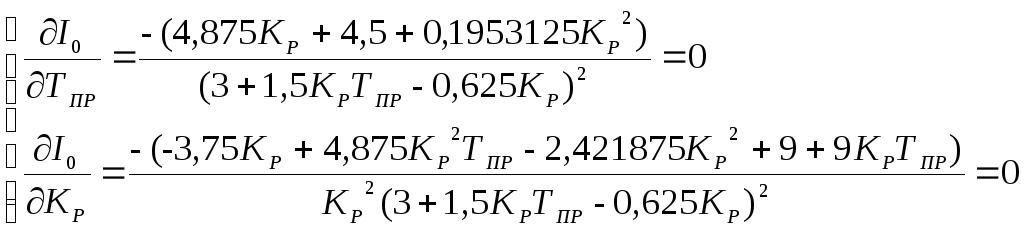(5.1.7)
Получаем систему уравнений, решая которую и найдём оптимальные значения параметров настройки регулятора.
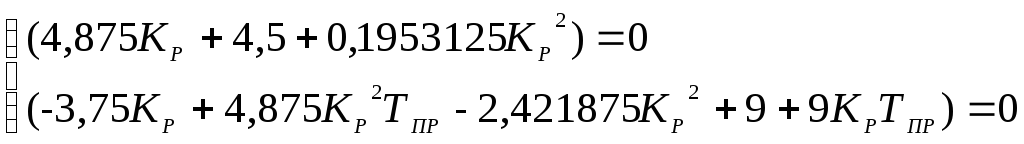(5.1.8)
Корни данной системы уравнений:
и 
(5.1.9)
Решение данной системы уравнений с математической точки зрения верное, но с точки зрения ТАУ коэффициент усиления регулятора не может быть отрицательным.
Значение же
квадратичной интегральной оценки при
данных корнях неопределенно (представляет
собой неопределённость вида
).
Таким образом при любом значении
квадратичной интегральной оценки и
какой-либо из полученных постоянных
времени (
или 
)
из выражения (5.1.12) получается два значения
, одно из которых
является корнем системы уравнений
(5.1.8) (оно является постоянным при
изменении 
), а второе значение 
зависит от 
.
Изменяя значение 
можно добиться
положительности значения коэффициента
усиления регулятора.
Поэтому необходимо
задаться положительным диапазоном
изменения параметров 
и 
[3].
В данной ситуации, в литературе [8],
рекомендуется задавать несколько
числовых значений одного из выбираемых
параметров (при жёстко заданных всех
остальных) и вычислять для каждого из
них значения 
.
В результате будет видно, при каких
значениях данного параметра получается
.
Мы же поступим несколько иначе, вычислим
коэффициент усиления всей системы
(через эквивалентный гармонический
сигнал и величину ошибки), затем рассчитаем
коэффициент усиления регулятора, после
чего, задаваясь значением 
,
постараемся получить данный коэффициент
усиления регулятора по выражению
(5.1.12) и сравним получившиеся интегральные
оценки при разных постоянных времени
(
и 
).
Коэффициент усиления всей системы на частоте эквивалентного гармонического сигнала:
,
откуда (5.1.10)
–коэффициент
усиления системы на частоте
, а на частоте
,
тогда коэффициент усиления регулятора:
. (5.1.11)
Из выражения
(5.1.6) выразим 
:
(5.1.12)
Решая данное квадратное уравнение получаем:
при 
при
|
|
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
|
|
|
0,3 |
0,5 |
0,7 |
0,9 |
|
|
-24 |
-24 |
-24 |
-24 |
-24 |
|
|
|
-0,96 |
-0,96 |
-0,96 |
-0,96 |
|
|
20 |
6,66 |
4 |
2,86 |
2,22 |
|
|
|
20 |
4 |
2,22 |
1,538 |
Таблица 5.1.1. Таблица 5.1.2.
Из таблиц видно, что при настройке регулятора на один и тот же коэффициент усиления, но с разными постоянными времени в системе, имеющей меньшую интегральную оценку переходный процесс будет протекать быстрее, нежели в системе с большей интегральной оценкой. Следовательно, выбираем следующие параметры настройки регулятора:
;
.