Вариант 23

Схема	k1	k2	k3	k4	K5	T1	T2	T3	T4	T5	ξ
a	4	1.5	4	2	0.7	0.4	0.3	0.5	0.15	0.9	0.5

Рисунок 1. Исходная схема

Задание 1. Определить передаточную функцию разомкнутой системы, привести её к каноническому виду.

Заданная схема состоит из 6-ти звеньев:

Рисунок 2. Исходная схема '

В каноническом виде схема будет выглядеть так:

Рисунок 3. Канонический вид

Данную схему можно перерисовать таким образом:

Рисунок 4. Упрощенная схема

Передаточная функция прямой цепи:

Передаточная функция разомкнутой цепи:

Степень астатизма ν=0. Коэффициент передачи K=1.71. Постоянные времени: T₁=0.15; T₂=√0.054=0.232379 – в числителе, T₃=0.389; T₄=0.4; T₅=√0.1157=0.34 – в знаменателе. Коэффициент колебательности: ξ=0.5

Задание 2. Частотная передаточная функция системы (s→j):

Причем: j²=-1; j³=-j; j⁴=1;

Вычислим точки пересечения годографа с осями. Для этого нужно P()=0 и Q()=0; Решая первое уравнение, P()=0 , находим :

Получили один действительный корень, значит, годограф будет пересекать мнимую ось в одной точке. Вычислим её:

Теперь Q()=0:

Особые точки АФЧХ приведены в таблице 1.

Таблица 1. Точки АФЧХ

	0	2.86	+∞
P	1.72	0	0
Q	0	-2.564	0

Задание 3. Годограф АФЧХ начинается в 4-м квадрате. К нулю стремится из 3-го квадрата (Рисунок 5).

Рисунок 5. Годограф САУ

Задание 4. Асимптотическая ЛАХ:

где K – общий коэффициент передачи разомкнутой системы;

T₁…T₅ – постоянные времени элементарных динамических звеньев структурной схемы, записанной в каноническом виде.

Асимптотическая ЛФХ:

Задание 5. Построение в масштабе ЛАХ и ЛФХ системы.

Начальный наклон ЛАХ: 0 дБ/дек

Значение ЛАХ при =1 равняется 20lgK, где K – общий коэффициент передачи разомкнутой системы. K=1.197, следовательно ЛАХ пересекает ось ординат на уровне 1.56188.

Степень астатизма ν=0, следовательно, наклон самой низкочастотной асимптоты равен 0 дБ/дек.

Строим таблицу значений сопрягающих частот

Таблица 2. Асимптотическая ЛАХ

T	0.4	0.389	0.34	0.232379	0.15
	2.5	2.57	2.95	4.3	6.6
Накл	-20	-20	-40	+40	+20

Асимптотическая ЛАХ, построенная по информации из таблицы 2 показана на рисунке 6:

Рисунок 6. Асимптотическая ЛАХ и ЛФХ

На рисунках 7 и 8 изображены в масштабе ЛАХ и ЛФХ системы соответственно:

Рисунок 7. ЛАХ

Рисунок 8. ЛФХ

Задание 6. Так степень астатизма равна 0 и характеристический полином разомкнутой системы имеет все корни в левой половине комплексной плоскости, то формулировка метода Найквиста будет выглядеть следующим образом: для того чтобы замкнутая САУ была устойчива необходимо и достаточно, чтобы годограф ее разомкнутой системы при изменении  от 0 до +∞ не охватывал точку с координатами [-1;j0].

Рисунок 9. Устойчивость по Найквисту

Из рисунка 9 видно, что частотный годограф не охватывает критическую точку, следовательно, замкнутая САУ будет устойчива.

Задание 7. Запас устойчивости по фазе характеризует удаление амплитудно-фазовой характеристики по дуге окружности единичного радиуса от критической точки и определяется углом между отрицательным направлением действительной оси и лучом, проведённым через начало координат и точку пересечения годографа с окружностью единичного радиуса, как показано на рисунке 10. Чтобы найти частоту среза — частоту, при которой годограф пересекает единичную окружность, нужно решить уравнение:

ω_ср=4 с^-1

Находим запас устойчивости по фазе:

Рисунок 10

Запас устойчивости по амплитуде будет равен 100%, так как АФХ не пересекает ось –π.

Задание 8. Передаточная функция замкнутой цепи может быть найдена по формуле:

; где ;

Следовательно, передаточная функция замкнутой системы будет равна:

Характеристический полином системы:

Определение устойчивости замкнутой системы методом Рауса. Таблица Рауса имеет следующий вид (таблица 3):

Таблица 3. Таблица Рауса

0.018	0.613	2.72
0.13	2	0
0.337	2.72	0	R3=a0/a1=0.138
0.95008	0	0	R4=a1/c13=0.386
2.72	0		R5=c13/c14=0.3547
0

Так как все элементы первого столбца положительны, то характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.

Определение устойчивости замкнутой системы методом Гурвица. Строим соответствующие заданной системе определители Гурвица:

Все определители Гурвица положительны, следовательно характеристический полином замкнутой системы имеет корни только в левой половине комплексной плоскости. Замкнутая САУ устойчива.

Задание 9. Характеристический полином системы:

После перехода s→j

Вещественная функция Михайлова:

Мнимая функция Михайлова:

Для построения годографа Михайлова необходимо решение уравнений:

Таблица 4. Точки годографа Михайлова

	0	2.3	3.92	5.36
Re	2.72	0	2.45	0
Im	0	3.019	0	-9.368

Годограф Михайлова изображен на рисунке 11:

Рисунок 11. Годограф Михайлова

Замкнутая САУ будет устойчивой тогда и только тогда, когда годограф Михайлова, при изменении  от 0 до +∞, начинаясь на положительной действительной полуоси последовательно и нигде не обращаясь в 0, пересекает 4 квадрата комплексной плоскости. Приведенный на рисунке график соответствует критерию Михайлова, следовательно, замкнутая САУ устойчива.

Задание 10. Передаточная функция ошибки будет иметь вид:

Теперь найдём коэффициенты ошибок:

Задание 11. Переходная функция

Найдем корни знаменателя:

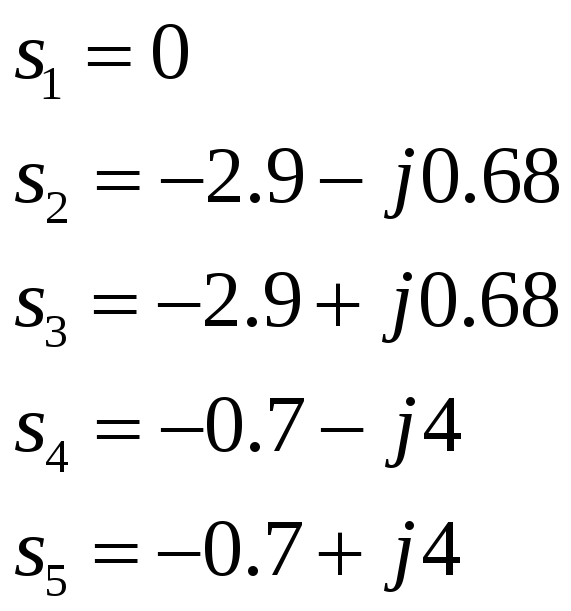
Составим таблицу:

Таблица 5. Коэффициенты переходной функции

s	0	-2.9-j0.681	-2.9+j0.681	-0.7-j4	-0.7+j4
M(s)/N’(s)	0.901	-0.121-j0.007	-0.121+j0.007	-0.329-j0.0066	-0.329+j0.0066

После подстановки получим:

График данной функции будет выглядеть так:

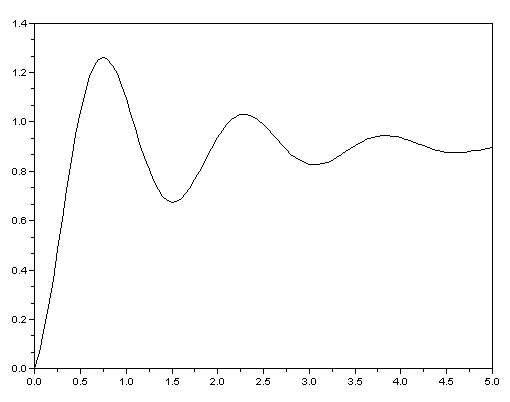
Рисунок 12. Переходная функция

Из рисунка видно, что время регулирования t_р5 с, а перерегулирование:

2. Задание на проектирование и порядок выполнения работы

Для структурной схемы САУ, соответствующей выбранному варианту,

выполнить следующие действия:

1)Избавиться от всех перекрестных параллельных и обратных связей,

привести структурную схему к стандартному виду. Определить

передаточную функцию разомкнутой системы, записать ее в стандартной

форме. Определить степень астатизма системы.

2)Определить амплитудно-фазовую, вещественную и мнимую частотные

характеристики разомкнутой системы.

3)Построить годограф АФЧХ разомкнутой системы.

4)Найти выражения для асимптотической ЛАЧХ и ЛФЧХ разомкнутой

системы.

5)Построить в масштабе ЛАЧХ и ЛФЧХ разомкнутой системы.

6)Определить устойчивость замкнутой САУ с помощью критерия

Найквиста и логарифмических частотных характеристик.

7)Найти запасы устойчивости системы по фазе и по амплитуде.

8)Найти передаточную функцию замкнутой системы и проверить выводы

пункта 6 с помощью алгебраических критериев Рауса и Гурвица.

9)Проверить выводы пункта 6 с помощью частотного критерия Михайлова.

10)Найти коэффициенты C0, C1, C2 ошибок системы.

11)Построить с помощью ЭВМ переходную функцию замкнутой системы

и оценить основные показатели качества регулирования

(перерегулирование и время регулирования) в системе.

Литература

1)Бесекерский В.А., Попов Е.П. Теория систем автоматического управления:

учебное пособие. – С-П.: Профессионал, 2004. - 752 с.

2)Пупков К.А., Егунов Н.Д. Методы классической и современной теории

автоматического управления: уч. для вузов в 5 томах. – М: изд. МГТУ им.

Н.Э.Баумана, Т.1 – Математические модели, динамические характеристики и

анализ САУ, 2004. - 656с.

3)Пупков К.А., Егунов Н.Д. Методы классической и современной теории

автоматического управления: уч. для вузов в 5 томах. – М: изд. МГТУ им.

Н.Э.Баумана, Т.3 – Синтез регуляторов систем автоматического управления,

2004. - 616с.

4)Ротач В.Ф. Теория автоматического управления: учебник для вузов. – М.:

изд. МЭИ, 2004. – 400с.

5)Душин С.Е. Теория автоматического управления. - М.: Высшая школа,

2005. – 567с.

6)Афанасьев В.К. и др. Математическая теория конструирования систем

управления. - М.: Высшая школа, 2000.-574 с.