курсовая работа / ВАРИАНТ №50

Задание

1. Линейная система

1.1. Упростить систему

1.2 Посчитать устойчивость

1.3. Построить переходный процесс

1.4. Построить АЧХ

1.5. Построить ЛАЧХ и ЛФЧХ

2. Нелинейная система

2.1. Построить фазовый портрет

3. Дискретная система

3.1. Z–преобразование

3.2. ω–преобразование

3.3. λ–преобразование

3.4. Проверить систему на устойчивость

3.5. Построить переходный процесс

3.6. Построить ЛАЧХ и ЛФЧХ

Исходные данные

ВАРИАНТ №50

Рис. 1. Структурная схема системы

W₁(p) = 1

1. Расчет линейной системы.

1.1. Упрощение системы.

По правилу преобразования структурных схем получим передаточную функцию

разомкнутой системы

Общая передаточная функция замкнутой системы с отрицательной обратной связью

После подстановки и преобразований передаточная функция замкнутой системы примет

следующий вид:

1.2. Проверка на устойчивость замкнутой системы.

1.2.1. По теореме устойчивости Ляпунова. Для того, чтобы автоматическая система,

описываемая линейными уравнениями с постоянными коэффициентами, была

устойчивой необходимо и достаточно, чтобы веществ. корни дифференциального

уравнения были отрицательными, а комплексные корни имели отрицательную

реальную часть.

Найдем корни характеристического уравнения с помощью Mathcad

Т.к. характеристическое уравнение системы имеет все корни с отрицательными вещественными частями, то данная система устойчивая.

1.3. Построение переходного процесса.

Построим график переходного процесса замкнутой системы с помощью Mathcad

Рис. 3. График переходного процесса замкнутой системы

По графику переходного процесса определим прямые оценки качества:

1. Установившееся значение h_уст =12,2т.к. , тогда интервал отклонения в 5% от установившегося значения будет соответствовать следующим величинам:

Δ₁ = h_уст – 0,025·h_уст = 11,895

Δ₂ = h_уст + 0,025·h_уст = 12,505

2. Время переходного процесса t_П = 75(с)

3. Перерегулирование:

4. Период колебаний Т = 4,6(с)

5. Частота колебаний ω = 0 ,2(рад/с)

6. Колебательность (число колебаний за время колебательного процесса) n = 4

7. Время нарастания регулируемой величины (время, за которое регулируемая величина

достигает максимального значения) t_H = 11(с)

8. Время первого согласования (время, когда регулируемая величина достигает первый

раз своего установившегося значения) t₁ = 76(с)

1.4. Построение амплитудно–частотной характеристики.

1. Запишем передаточную функцию разомкнутой системы:

2. Заменим в передаточной функции p на jω. После подстановки передаточная

функция примет следующий вид:

3. Запишем формулу для расчета АЧХ в Mathcad.

4. Строим амплитудно–частотную характеристику разомкнутой системы с поиощью

Mathcad.

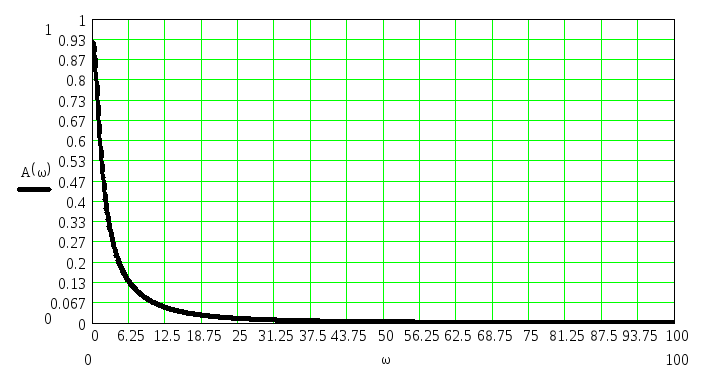
Рис. 4. Амплитудно–частотная характеристика.

По графику амплитудно–частотной характеристики определим косвенные оценки

качества:

1. Максимальное значение амплитуды А_max = 0,924 т.к

2. Резонансная частота (частота, при которой амплитуда максимальна) ω_Р = 0 (рад/с)

3. Частота среза ω_СР = 0,31 (рад/с)

1.5. Построение ЛАЧХ и ЛФЧХ.

1. Запишем передаточную функцию разомкнутой системы.

2. Заменим в передаточной функции p на jω. После подстановки передаточная

функция примет следующий вид:

3. Разобьем передаточную функцию на:

– вещественную часть

– мнимую часть

4. Записываем выражение для амплитудно–частотной A(), фазо–частотной () и

логарифмической амплитудно–частотной D() и фазо–частотной характеристик:

Построим графики частотных характеристик.

Рис. 5. Фазо–частотная характеристика.

Для построения ЛАЧХ системы, определим частоты излома:

Рис. 6. Логарифмическая амплитудно–частотная характеристика

Рис. 7. Логарифмическая фазо–частотная характеристика.

– по графику ЛФЧХ определим запас устойчивости по фазе γ = 47⁰

– по графику ЛАЧХ определим запас устойчивости по амплитуде m = 55дб

3. Расчет дискретной системы.

3.1. Z–преобразование.

Рис. . Структурная схема непрерывно–дискретной системы

1. Передаточная функция линейной системы:

2. Передаточная функция дискретной системы

где Т – период дискретности системы

3.