Введение

Система предназначена для стабилизации движения самолета по тангажу.

Рисунок 1

Функциональная схема изображена на рис.1.

На схеме обозначено: Х- сила лобового сопротивления; Y- подъемная сила; G - сила тяжести; Mz - суммарный момент, приложенный к самолету относи­тельно оси z; P — сила тяги; в_с - угол наклона траектории; - углы атаки и тангажа; V - вектор скорости.

Бортовая система управления по каналу тангажа включает датчики информа­ции, автопилот, выполняющий функцию регулятора, и привод рулей высоты. В качестве датчиков информации используются датчик углового положения (ДУП) и датчик угловой скорости (ДУС).

Сигнал с ДУП в виде напряжения , пропорционального действительному значению угла тангажа самолета , сравнивается с напряжением задатчика , так что на автопилот поступает напряжение , пропорциональное отклонению угла тангажа от требуемого значения. Сигнал с ДУС представляется напряже­нием , пропорциональным угловой скорости самолета относительно поперечной оси z.

Уравнения возмущенного движения самолета, линеаризованные относитель­но некоторого режима полета, имеют вид:

где - отклонение угла атаки от номинального значения; - отклонение угла по­ворота руля высоты; - приведенное внешнее возмущение (безразмерная величи­на), природой которого могут быть вертикальные составляющие порывов ветра, сброс груза, находящегося не в центре тяжести самолета и др.

Система работает следующим образом. При действии внешнего возмущения изменяется суммарный момент M_z , что приводит к изменению угла тангажа са­молета и появлению сигналов и с датчиков информации. По этим сигна­лам в автопилоте формируется управляющее напряжение и на рулевой привод, который изменяет угловое положение руля высоты так, что возникающий при этом аэродинамический момент компенсирует изменение момента M_z , и угол тангажа самолета становится близким к заданному.

Структурная схема системы стабилизации угла тангажа самолета:

1 АНАЛИЗ ЛИНЕЙНОЙ СУ

1.1 Упрощение структурной схемы СУ

Избавимся от последовательного соединения звеньев:

Далее избавимся от внутреннего встречно-параллельного участка схемы:

k_v

Избавимся от последовательного соединения звеньев:

Далее избавимся от внутреннего встречно-параллельного участка схемы:

Т.к. на схеме обозначено:

- передаточное число (коэффициент передачи) автопилота по углу тангажа;

- передаточная функция рулевого привода;

- передаточная функция самолета по угловой скорости тангажа;

- передаточное число автопилота по угловой скорости тангажа.

Для передаточной функции разомкнутой системы можно записать

Где ; ;;

Передаточная функция замкнутой системы имеет вид

Где ; ; ; ;

; ;; ; ;

При этих значение для коэффициентов характеристического уравнения получим:

; ; ; ; ;

Тогда получим:

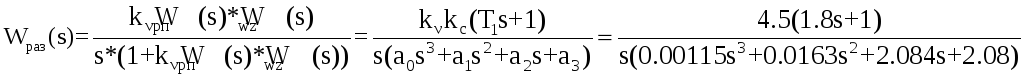
1.2 Построение АФЧХ системы

Получим частотную форму записи передаточных функций.

Выделим действительную и мнимую части замкнутой системы:

–

–

+

+

Выделим действительную и мнимую части разомкнутой системы:

+

+

+

+

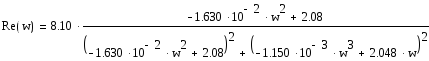
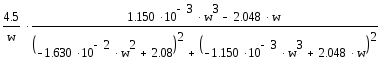
Построим АФЧХ замкнутой системы:

График 1 – АФЧХ

Для построения графика использовались дискретные значения

1.3 Построение АЧХ, ФЧХ и ЛАЧХ системы

1.3.1 построение АЧХ

График 2 – АЧХ

1.3.2 Построение ФЧХ

График 3 – ФЧХ

1.3.3 Построение ЛАЧХ

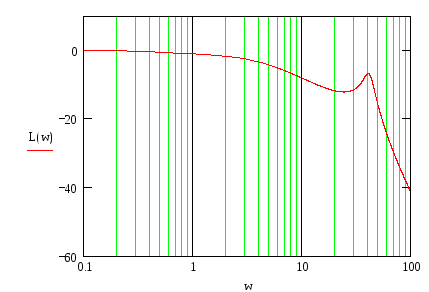
График 4 – ЛАЧХ

1.4 Исследование устойчивости СУ

Определим устойчивость СУ по критерию Найквиста.

Определим устойчивость разомкнутой системы по критерию Ляпунова.

Устойчивость по Ляпунову означает, что все корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости.

Запишем характеристическое уравнение разомкнутой системы:

Найдем корни характеристического уравнения для замкнутой системы:

Так как все вещественные части корней отрицательны, то корни характеристического уравнения находятся в левой полуплоскости комплексной плоскости, а это означает устойчивость системы.

По критерию Найквиста: если система в разомкнутом состоянии устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы для не охватывали точку с координатами (-1: j0).

Построим годограф Найквиста:

График 5 – Годограф Найквиста

Устойчивая СУ с астатизмом n-го порядка.

1.5 Определение запасов устойчивости СУ

Построим ЛАЧХ и ЛФЧХ разомкнутой системы:

ΔL

Δ

ΔL=9 – Запас по амплитуде.

- запас по фазе.

1.6 Построение переходного процесса и оценка качества СУ

h_уст

t_р

По графику

Перерегулирование

В данном случае перерегулирование равно 0 т.к. процесс монотонный.

- время за которое процесс входит в 5%-ую трубку.

Заключение: с учетом этих показателей можно сделать вывод, что качество управления СУ достаточно хорошее и не требует дополнительной коррекции, так как перерегулирование и время регулирования малы.

2 АНАЛИЗ НЕЛИНЕЙНОЙ СУ

2.1 Построение по заданной структурной схеме СУ ее фазового портрета

Нелинейный элемент:

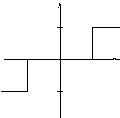
Разомкнем систему перед нелинейным элементом, перенося на новый вход системы регулирующее воздействие. Получим следующую структурную схему.

Упростим структурную схему, избавившись от встречно-параллельного и последовательных соединений

Структурная схема примет вид:

u-X

Или

X

Учитывая коэффициенты получим передаточную функцию линейной части.

; ;; ; ;;

Далее вынесем из числителя 1.944 и из знаменателя 0.000138

Теперь избавимся от многочлена числителя, для этого умножим числитель и знаменатель на :

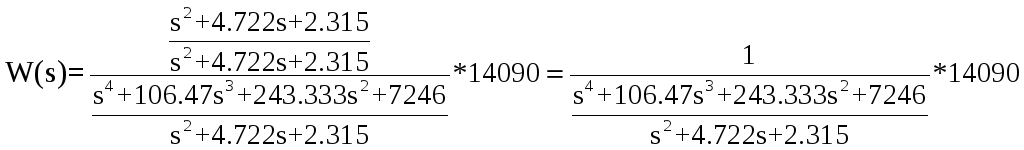
Остатком можно пренебречь, в итоге имеем следующее выражение для передаточной функции:

Преобразуем:

Окончательное выражение для передаточной функции:

По определению передаточной функции.

Следовательно:

s(0.0199s+1)X=281.574X_i

s(0.0199s+1)X=281.574F(u-X)

Будем считать, что на вход системы подано постоянное воздействие , тогда перейдем от самих величин к их отклонениям относительно постоянного входного воздействия. Введем обозначения.

С учетом этого получим следующую систему уравнений.



Разделив уравнение (1) на (2) и исключив таким образом время, получим дифференциальное уравнение фазовых траекторий:

Решение данного уравнения будет строиться исходя из заданной нелинейности. В данном случае нелинейной частью системы является трехпозиционное реле .

(3)

В соответствии с системой (3) запишем уравнение, с учетом того, что функция является нечетной, т.е. симметрична относительно начала координат:

Пусть в начальный момент времени система выведена в точку М₀ с координатами (х_0, у₀). Проинтегрируем вышеприведенное выражение от х₀ до х и от у₀ до у.

Найдем решение каждого из уравнений системы по очереди:

1) .

Т.к. изначально система выведена в точку фазовой плоскости М₀ с координатами (x₀,y₀) , то интегрирование будет: от x₀ до x ; от y₀ до y.

Найдем решение каждого уравнения:

1)

получим

2)

- отрезок прямой для интервала

3)

Задаваясь различными значениями "у" построим фазовый портрет системы.

1-ая прямая

2-ая прямая

3-я прямая

4-ая прямая

5-ая прямая

Т.к. по данному фазовому портрету сложно судить об устойчивости системы построим фазовый портрет более детально.

- передаточная функция линейной части системы.

В данной передаточной функции - идеальное интегрирующее звено и - апериодическое звено 1-го порядка.

Линейная часть системы будет описываться уравнением:

Характеристика нелинейного элемента разбивается на три линейных участка и для каждого из них составляется дифференциальное линейное уравнение:

Для фазовой плоскости введем координаты y и z=dy/dz. Исключим в предыдущих уравнениях время t.

(***)

Разделяя переменные и интегрируя, получим уравнения фазовых траекторий для участков 1-3 нелинейной характеристики.

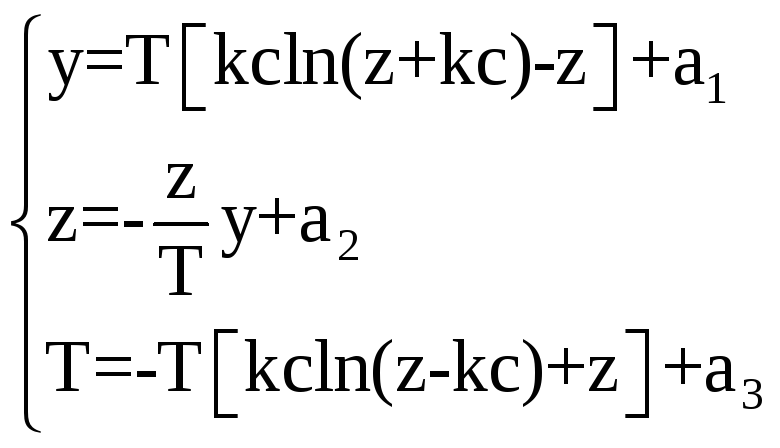
Первоначально на фазовой плоскости наносят линии переключения, разделяющие плоскость на три области. Это линии от одного участка нелинейной характеристики к другому.

Затем строят фазовые траектории. При этом должно учитываться правило: в верхней полуплоскости фазовая траектория движется слева направо, в нижней справа налево.

В целом фазовые траектории принимают спиралевидную форму, что соответствует затухающим колебательным процессам.

Однако колебательный процесс затухает не до нуля, а до некоторого значения внутри интервала , определяемого зоной нечувствительности. Таким образом имеем отрезок особых равновесных состояний.

Начальные условия определяют фазовую траекторию, по которой пойдет переходной процесс.

Реализуем программу решения системы уравнений (***) в mathcad.

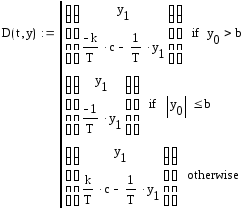
Построим фазовый портрет и переходную характеристику нелинейной СУ.