МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПИЩЕВЫХ ПРОИЗВОДСТВ.

Кафедра «Автоматизация

технологических процессов»

Курсовая работа по ТАУ

Определение динамических характеристик объекта

и расчёт одноконтурной АСР.

Студент: Сурнин О.А.

Группа: 07-ИУ-4

Преподаватель: Полянская П.В.

Москва 2009 г.

Цель работы: экспериментальное получение кривой разгона объекта регулирования и её обработка для расчёта коэффициентов дифференциального уравнения объекта; расчёт оптимальных параметров настройки ПИ-регулятора.

Структурная схема АСР:

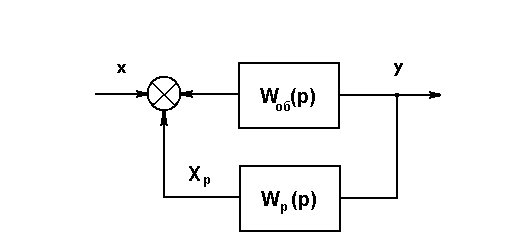
Вход объекта x – напряжение питания U,В

Выход объекта y – температура в печи , С

Схема лабораторного стенда:

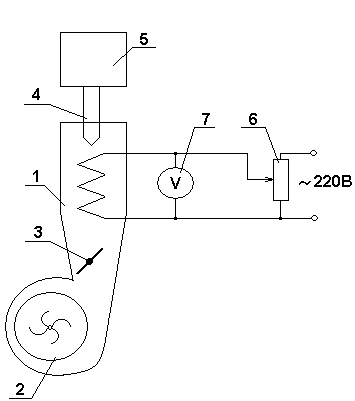
1 – электрическая печь

(объект управления)

2 – вентилятор

3 – заслонка

4 – термопара

5 – регистрирующий прибор

6 – автотрансформатор

7 – вольтметр

Методика получения кривой разгона:

1. Убедиться, что в печи – установившийся режим y(t) = const при определенном значении напряжения

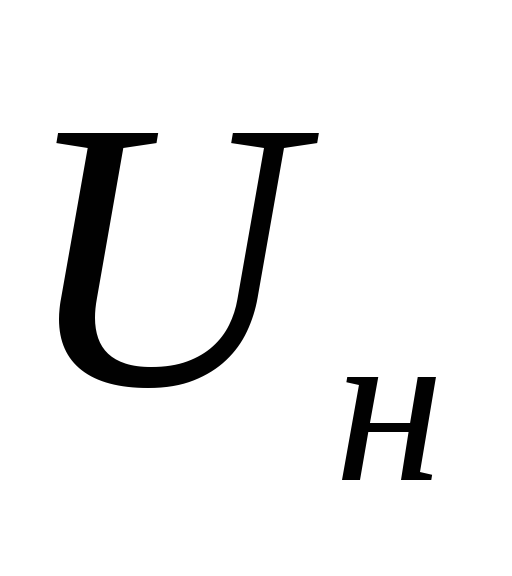
2. С помощью автотрансформатора изменить скачком напряжение питания печи на величину

3. На диаграмме регистрирующего прибора записать кривую изменения температуры с момента изменения напряжения до наступления нового установившегося режима.

Обработка экспериментальной кривой разгона.

Выделяем время запаздывания t = 4мин.

Время переходного процесса делим на равные интервалы и соответствующие ординаты кривой разгона вносим в таблицу.

Таблица 1

N Точки	T мин	, oС	y = , oC	h=y/x , oC/B
1	0,00	78	0	0
2	2	93	15	0,25
3	3,6	127	49	0,82
4	5,2	180	102	1,7
5	6,8	217	139	2,31
6	8,4	234	156	2,6
7	10	246	156	2,6
8	11,6	258	180	3
9	13,2	261	183	3,05

Коэффициент усиления объекта

y() 183[ ^oC ] ^oC

K = = = 3.05

x 60[ B ] B

x = U = 60 B

Далее расчёты производятся на ЭВМ, пакет «TAU», который содержит пять этапов:

Этап 1.

Расчёт коэффициентов дифференциального уравнения методом интегральных площадей (метод Симою)

Исходные данные:

интервал разбиения оси абсцисс кривой разгона 1.6

установившееся значение параметра 3.05

число точек при расчёте кривой разгона 9

Проверка правильности аппроксимации переходной функции.

Рисунок 2.

Результаты расчёта :

Коэффициенты дифференциального уравнения объекта:

1-й коэф. = 4.93

2-й коэф. = 8.23

3-й коэф. = 3.80

Динамические характеристики объекта:

дифференциальное уравнение объекта

3.8y^’’’ (t)+ 8.23y^’’ (t) + 4.93y^’ (t) + y (t) =3.05x (t –0.4)

передаточная функция

Этап 2.

Проверка точности аппроксимации. ЭВМ находит решение дифференциального уравнения, сравнивает экспериментальную и расчетную переходные функции.

Исходные данные:

длительность переходного процесса 13.2 (мин)

шаг печати результатов 1.6

установившееся значение параметра 3.05

Результаты расчёта :

Кривая разгона	Расчёт h(t)	Ошибка ( % )
0	0	0
0,25	0,2276	8,9545
0,82	0,9192	12,0990
1,7	1,6554	2,6216
2,31	2,2241	3,7190
2,6	2,5995	0,0192
2,8	2,8231	0,824
3,0	2,9457	1,8115

Максимальная ошибка 12.0990

По полученным результатам строим расчётную и экспериментальную переходные функции (см. Рисунок 2.).

Запишем выражения для расчётных характеристик объекта:

; заменим р на (-i-m)

M(m,) =

Этап 3.

Расчёт частотных характеристик объекта на ЭВМ.

Расчёт производится 2 раза для m = 0 и m = 0,221 ( расширенная частотная характеристика).

Исходные данные:

степень колебательности 0,00 ; 0,221

нижняя граница частоты 0,00

верхняя граница частоты 0,00

передаточный к-т объекта 3.05

время запаздывания 0,4

1-ой к-т д/у 4.93

2-ой к-т д/у 8.23

3-ой к-т д/у 3.8

Результаты расчёта:

m = 0			m = 0,221
частота	РАЧХ(АЧХ)	-(РФЧХ)(ФЧХ)	частота	РАЧХ	-(РФЧХ)
0,3153	2,1089	90,0021	0,2837	2,9384	90,0033
0,3758	1,8990	104,2340	0,3267	2,7384	102,9087
0,4363	1,5881	117,1736	0,3698	2,5165	115,1557
0,4968	1,3645	128,8826	0,4128	2,2667	126,6481
0,5574	1,1705	139,4732	0,4558	2,0609	137,3457
0,6179	1,0050	149,0760	0,4989	1,8472	147,2543
0,6784	0,8651	157,8205	0,5419	1,6503	156,4135
0,7389	0,7472	165,8242	0,5849	1,4724	164,8803
0,7995	0,6480	173,1899	0,6279	1,3136	172,7221
0,8600	0,5643	180,0046	0,6710	1,1729	180,0029

По полученным данным строим графики (см. рис. 4).

Расчётные данные дополняем известными значениями M(=0) = 3,05; (=0) = 0

Частотные характеристики объекта:

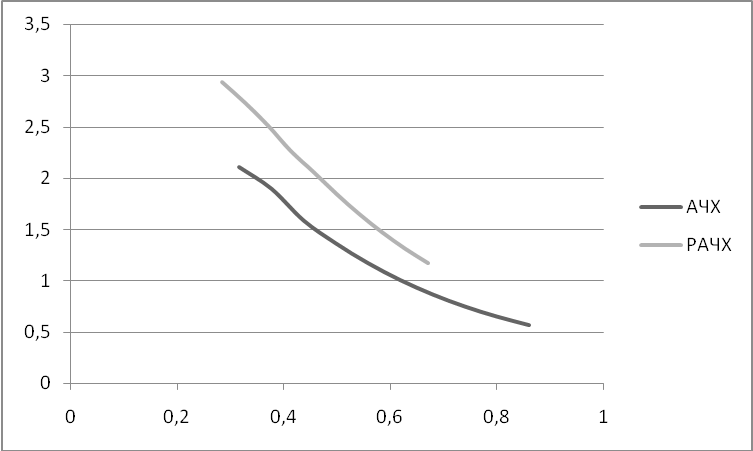
Рисунок 3.

Рисунок 4.

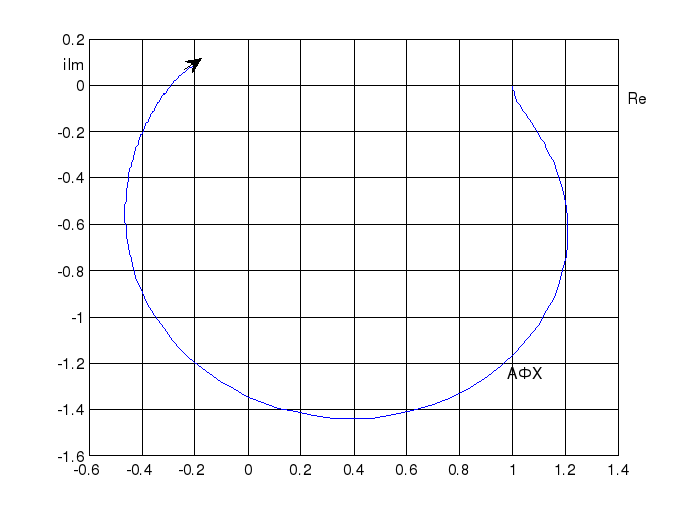
Рисунок 5.

Расчёт оптимальных параметров настройки ПИ – регулятора.

Для регулирования объекта выбран ПИ – регулятор .

ПИ – закон регулирования:

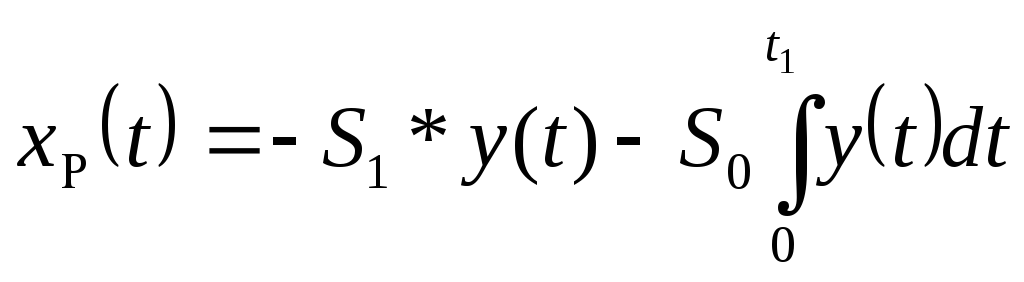
Оптимальными настройками считаем значения S₁ и S₀, соответствующие минимальному значению интегрального квадратичного критерия качества переходного процесса.

при степени колебательности не ниже заданной (m = 0,221).

Расчёт настроек ПИ – регулятора методом незатухающих колебаний (Циглера – Никольса)

Определяем S, при которой в системе, состоящей из данного объекта и ПИ – регулятора, будут незатухающие колебания.

Сначала из 2-го уравнения определим (частоту незатухающих колебаний)

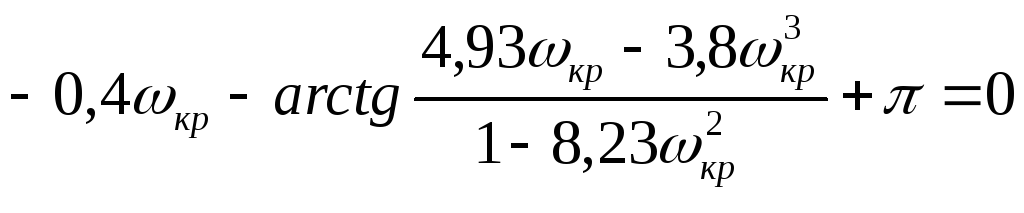
Расчёт настроек ПИ – регулятора по приближенным формулам:

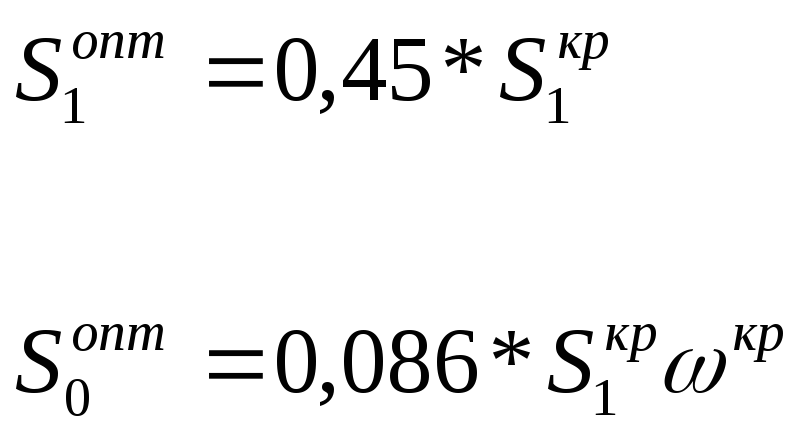
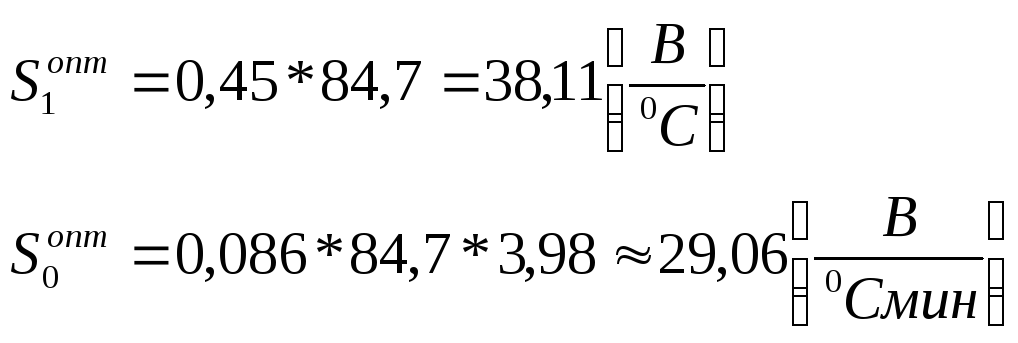
Этап 4. Расчёт на ЭВМ оптимальных параметров настройки ПИ – регулятора (методом расширенных частотных характеристик).

Исходные данные:

с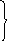тепень колебательности 0,221

начальная частота 0,28368

шаг изменения частоты 0,04303 из Этапа 3.

число точек 10

Результаты расчёта

частота	S0	S1
0,2837	0,1013	0,0745
0,3267	0,1220	0,1594
0,3698	0,1397	0,2475
0,4128	0,1523	0,3376
0,4558	0,1578	0,4286
0,4989	0,1541	0,5193
0,5419	0,1391	0,6084
0,5849	0,1105	0,6946
0,6279	0,0658	0,7768
0,6710	0,0024	0,8535

Оптимальные параметры настройки:

S₀=0,154 , S₁=0,519 , - рабочая частота

По полученным данным строим график кривой равной степени колебательности:

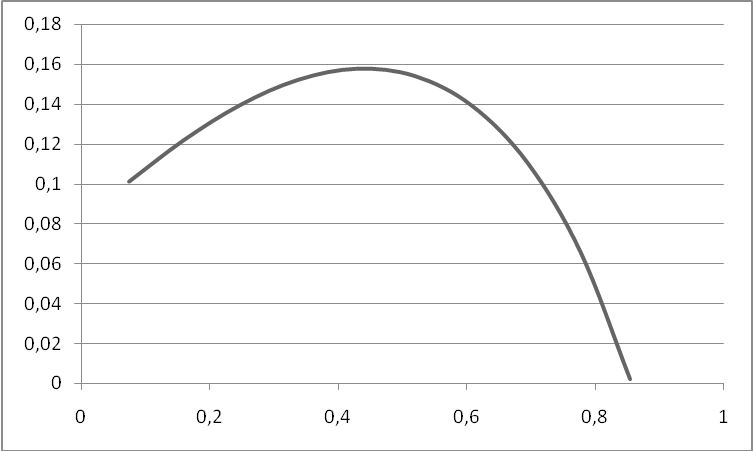
Этап 5. Расчёт переходного процесса.

Исходные данные:

длительность переходного процесса 13,2

время запаздывания 0,4

амплитуда входного воздействия 1

коэффициент усиления объекта 3,05

коэффициенты дифференциального уравнения объекта : 1-ый - 4,93

2-ой - 8,23 3-ий - 3,8

Оптимальные параметры настройки

S₀=0,154 , S₁=0,519

Результаты расчёта:

Время	Переходный процесс
1,68	0,1395
3,36	0,7730
5,04	1,2333
6,72	1,1521
8,4	0,6653
10,08	0,1243
11,76	-0,1962
13,44	-0,2317
15,12	-0,0902
16,8	0,0699
18,48	0,1444
20,16	0,1191
21,84	0,0429
23,52	-0,0245
25,2	6,8318

Интегральный критерий качества : 6,8318

На основе полученных данных строим график переходного процесса.

Из графика определяем показатели качества переходного процесса.

Из графика определяем показатели качества переходного процесса.

Степень затухания:

Максимальное динамическое отклонение:

Время регулирования – для его определения задаёмся допустимым отклонением

от максимального отклонения Kx.