
- •Федеральное агентство по образованию
- •Государственное образовательное учреждение высшего профессионального
- •Образования
- •Уфимский государственный авиационный технический университет
- •Система автоматического регулирования частотой вращения газотурбинного двигателя
- •К курсовой работе по дисциплине Основы автоматического управления
- •4041.235___.000 Пз
- •Введение
- •1. Передаточные функции элементов системы управления и составление структурной схемы
- •2. Определение передаточных функций разомкнутой и замкнутой системы. Характеристические полиномы
- •3. Построение области устойчивости замкнутой системы методом d-разбиения по неизвестному коэффициенту усиления
- •4.Анализ устойчивости исходной системы
- •4.1. Устойчивость разомкнутой системы по корням характеристического уравнения.
- •4.2. Анализ устойчивости исходной системы по критерию Гурвица.
- •4.3. Устойчивость системы по критерию Михайлова.
- •4.4. Устойчивость системы по критерию Найквиста.
- •5. Построение лачх и лфчх исходной разомкнутой системы.
- •6. Построение желаемой лачх с учетом требуемых значений быстродействия, перерегулирования и точности.
- •7. Построение лачх корректирующего устройства, определение его передаточной функции и расчет параметров.
- •Расчет корректирующего устройства.
- •8. Определение статистической ошибки, ошибок по скорости и по ускорению скорректированной системы, запасы устойчивости.
- •9. Расчет переходной характеристики, моделирование сау.
- •Заключение
- •Бесекерский в.А., Попов е.П. Теория систем автоматического управления. – сПб.: Профессия, 2003. – 128-131с, 230с, 389-395с.
- •Курс лекций по тау / е.Н.Шевяхов, Уфа, 2006.
- •Воронов а.А. Теория автоматического управления. Часть I. Теория линейных систем автоматического управления. – м.: Высшая школа, 1986.
4.Анализ устойчивости исходной системы
4.1. Устойчивость разомкнутой системы по корням характеристического уравнения.
Решая
уравнение
![]() получим:
получим:
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Для определения
устойчивости замкнутой системы решим
уравнение
![]() .
.
Отсюда получим:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Все вещественные части корней отрицательны, что говорит об устойчивости замкнутой системы.
4.2. Анализ устойчивости исходной системы по критерию Гурвица.
Используя критерий Гурвица оценим устойчивость замкнутой системы. Для характеристического уравнения
![]() (8)
(8)
составим матрицу Гурвица
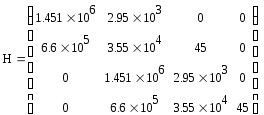
Найдем значения главных определителей.
![]() ,
,
![]()
![]()
![]() .
.
Как видно, все определители Гурвица больше нуля, значит система является устойчивой по критерию Гурвица.
4.3. Устойчивость системы по критерию Михайлова.
Для оценки
качества устойчивости по критерию
Михайлова построим характеристический
годограф (вектор) (5)
![]() замкнутой
системы.
замкнутой
системы.
Меняя ω от 0 до
![]() строим годограф Михайлова:
строим годограф Михайлова:

Рис.4.а–Годограф Михайлова.
где
![]() -мнимая
часть
-мнимая
часть![]() ,
,![]() -действителная
часть
-действителная
часть
![]() .
.

Рис.4.б–Годограф Михайлова.
Из рисунков видно, годограф Михайлова начинается на положительной полуоси, и последовательно проходит против часовой стрелки 4 квадрантов комплексной плоскости, уход в бесконечность в 4-ом квадранте. Условие устойчивости критерия Михайлова выполняется.
4.4. Устойчивость системы по критерию Найквиста.
Этот критерий
позволяет судить об устойчивости
замкнутой САУ по виду АФЧХ разомкнутой
САУ. Путем
замены
![]() в
передаточной функции разомкнутой
системы, получим:
в
передаточной функции разомкнутой
системы, получим:
 (9)
(9)
Меняя ω от 0 до
![]() строим годограф Найквиста:
строим годограф Найквиста:

Рис.5–Годограф Найквиста.
где
![]() -мнимая
часть
-мнимая
часть![]() ,
,![]() -действителная
часть
-действителная
часть
![]() .
.
Система имеет
астатизм первого порядка, следовательно,
при частоте стремящейся к нулю мнимая
часть устремляется к минус бесконечности.
Поэтому АФЧХ разомкнутой системы
дополняем окружностью бесконечного
радиуса R![]()
![]() .
Так как нулевой корень заменяем малым
вещественным отрицательным корнем, то
разомкнутую систему можно считать
устойчивой. Все это означает, что для
исследования устойчивости замкнутой
системы можно применять критерий
Найквиста. Из рисунка видно, что точка
(-1;j0) не охватывается годографом, значит
замкнутая система устойчива.
.
Так как нулевой корень заменяем малым
вещественным отрицательным корнем, то
разомкнутую систему можно считать
устойчивой. Все это означает, что для
исследования устойчивости замкнутой
системы можно применять критерий
Найквиста. Из рисунка видно, что точка
(-1;j0) не охватывается годографом, значит
замкнутая система устойчива.
Определим запасы устойчивости по фазе и амплитуде.

Рис.5–Годограф Найквиста и окружность единичного радиуса.
Запас по амплитуде: 0,36
Запас по фазе:
10,71 градусов.

5. Построение лачх и лфчх исходной разомкнутой системы.
Передаточная функция разомкнутой системы:
![]()
Определим постоянные времени и соответствующие им частоты.
T1= 0.02 w1=50 lg(w1)=1.699
T2 = 0.067 w2=14,92 lg(w2)=0.76
T3 = 1.333 w3=0.75 lg(w3)=-0.125
T4 =
2.16 w4=0.462 lg(w1)=-0.334
![]()
Логарифмические
частотные характеристики разомкнутой
системы строим с учетом требуемого
коэффициента усиления. Коэффициент
ошибки для астатической системы равен
![]() .
Откуда можно определить
.
Откуда можно определить![]() .
.
![]() ,
(10)
,
(10)
![]() .
(11)
.
(11)
Асимптотическая ЛАЧХ и ЛФЧХ изображены в приложении .
6. Построение желаемой лачх с учетом требуемых значений быстродействия, перерегулирования и точности.
Построение желаемой ЛАЧХ производится из следующих условий быстродействия, перерегулирования и точности: σ=30%, tр=3 c.
Из условия устойчивости системы определим частоту среза и запас по амплитуде системы [См. 1].

Требуемое
значение запаса по модулю![]() дБ и запаса по фазе
дБ и запаса по фазе
![]() .
.
Из
полученных условий строим желаемую
ЛАЧХ. Отметим точку
![]() и проведем через нее прямую с наклоном
–20дБ/дек, которая представляет собой
среднечастотную амплитуду желаемой
ЛАЧХ. Продолжим прямую до тех пор, пока
ординаты не станут равными L1
и L2.
Этим точкам соответствуют частоты
и проведем через нее прямую с наклоном
–20дБ/дек, которая представляет собой
среднечастотную амплитуду желаемой
ЛАЧХ. Продолжим прямую до тех пор, пока
ординаты не станут равными L1
и L2.
Этим точкам соответствуют частоты
![]() и
и
![]() .
Из этих данных определяем
.
Из этих данных определяем
![]() ,
,
![]() .
Низкочастотная область
.
Низкочастотная область  желаемой
ЛАЧХ совпадает с исходной ЛАЧХ:
желаемой
ЛАЧХ совпадает с исходной ЛАЧХ:
![]() .
Высокочастотную область проводят так,
чтобы через каждую 0,2 дек ломать на 20
дБ/дек, чтобы наклон желаемой ЛАЧХ в
конце совпало с исходной ЛАЧХ:
.
Высокочастотную область проводят так,
чтобы через каждую 0,2 дек ломать на 20
дБ/дек, чтобы наклон желаемой ЛАЧХ в
конце совпало с исходной ЛАЧХ:
![]() Она представлена в приложении .
Она представлена в приложении .
Составим передаточную функцию разомкнутой системы для желаемой САУ, получим:
![]() (11)
(11)
После этого построим ЛФХ желаемой системы (см. приложение) и определим запасы устойчивости по амплитуде и по фазе, и сравним их с запасами устойчивости, полученными из номограммы.
![]()
![]() ,
,
Запас по фазе
![]() ,
запас устойчивости по амплитуде равен
9 Дб. Требуемые запасы выполняются.
,
запас устойчивости по амплитуде равен
9 Дб. Требуемые запасы выполняются.
