2 Анализ устойчивости системы

При проверке системы на устойчивость, сначала необходимо проверить выполнение необходимого условия устойчивости, согласно которому все коэффициенты характеристического уравнения должны быть строго положительны.

Характеристическое уравнение

Как видим, все коэффициенты положительны, следовательно, необходимые условие устойчивости выполняется.

Оценим устойчивость системы различными методами

2.1 Прямой метод

Передаточная функция замкнутой системы

Найдем полюса передаточной функции, для этого вычислим корни характеристического уравнения

Полюса передаточной функции

Так как все полюса передаточной функции лежат в левой полуплоскости комплексной плоскости, то система является устойчивой.

2.2 Частотный критерий Найквиста

Построим логарифмическую амплитудно – частотную L(ω) и фазо – частотную φ(ω) характеристики в совмещенной системе координат для разомкнутой системы. Воспользуемся программой PSM.

Рисунок 2 Логарифмическая амплитудно – частотная L(ω) и фазо – частотна φ(ω) характеристики разомкнутой системы

Из графиков найдем частоту среза и значение фазо – частотнной характеристики

Так как на частоте среза фазо – частотная характеристика лежит выше , -180° то система является устойчивой.

Оценим запас устойчивости

2.3 Алгебраический критерий устойчивости Гурвица

Необходимо из коэффициентов характеристиче­ского уравнения составить определитель Гурвица, размерность которого равна порядку системы.

Порядок системы, равен четырем (т.к. четыре корня в характеристическом уравнении).

Выразим коэффициенты характеристического уравнения системы

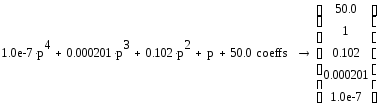
Составляем определитель Гурвица

Далее необходимо вычислить значение определителя Гурвица и всех его диагональных миноров

Так как определитель Гурвица и все его диагональные миноры положительные, следовательно, система устойчива.

3 Провести синтез последовательного корректирующего звена

Для достижения необходимых результатов по качеству системы, рассчитаем последовательное корректирующее звено.

Строим график линеаризованной ЛАХ, далее, строим ЛАХ скорректированной системы и вычитаем из нее ЛАХ исходной. Получаем ЛАХ корректирующего звена.

Частоты сопряжения линеаризованной системы

Для заданного значения перерегулирования, определяем частоту среза

Частоты сопряжения и постоянные времени скорректированной системы

Передаточная функция корректирующего звена

Построим переходный процесс нескорректированной и скорректированной систем.

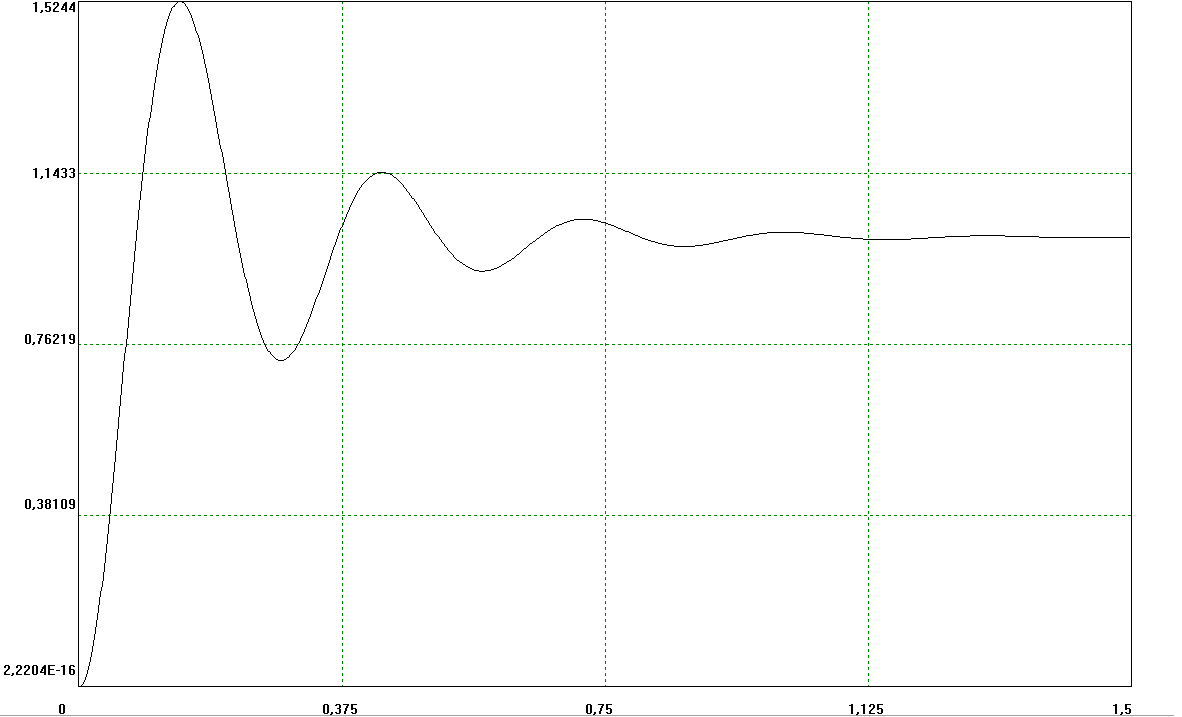
Рисунок 4 Переходная функция нескорректированной системы

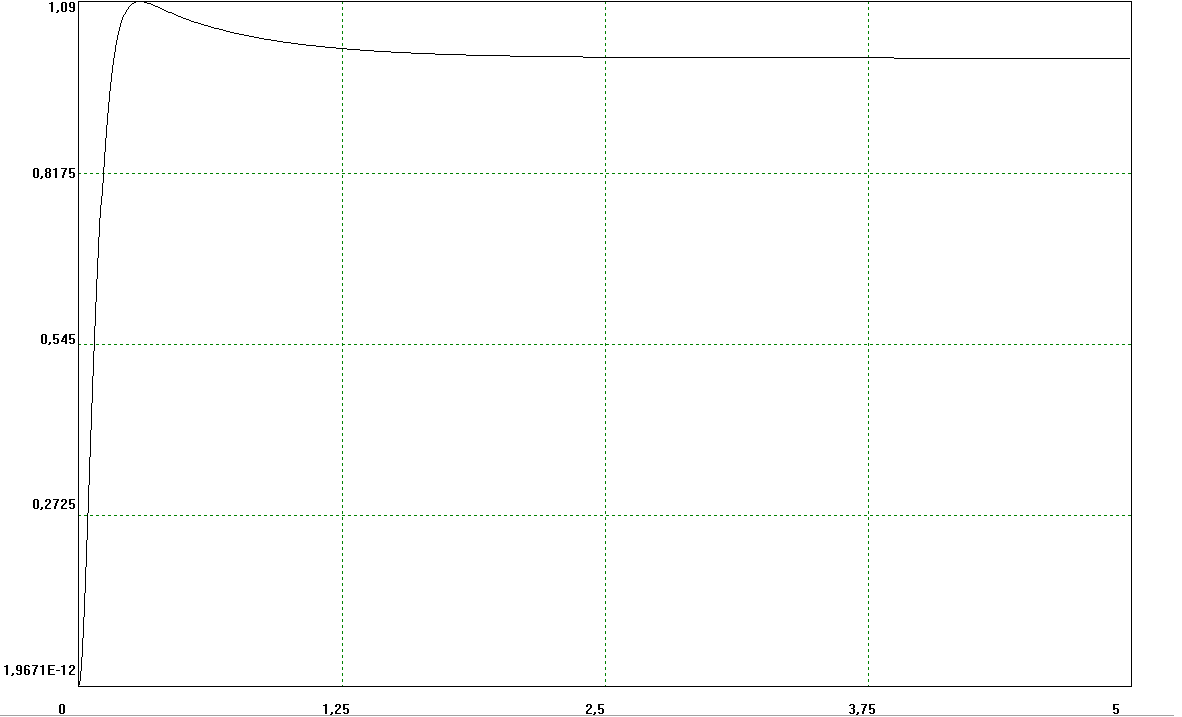
Рисунок 5 Переходная функция скорректированной системы

По графику определяем перерегулирование системы

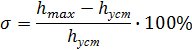
А так же время регулирования системы

Таким образом, скорректированная система полностью удовлетворяет всем поставленным условиям. Система прошла проверку на устойчивость, по нескольким критериям, а с помощью корректирующего звена удалось добиться значительного уменьшения перерегулирования и времени регулирования системы.

Определим критическое время запаздывания скорректированной системы. Для этого, построим логарифмическую амплитудно – частотную L(ω) и фазо – частотную φ(ω) характеристики в совмещенной системе координат для скорректированной системы.

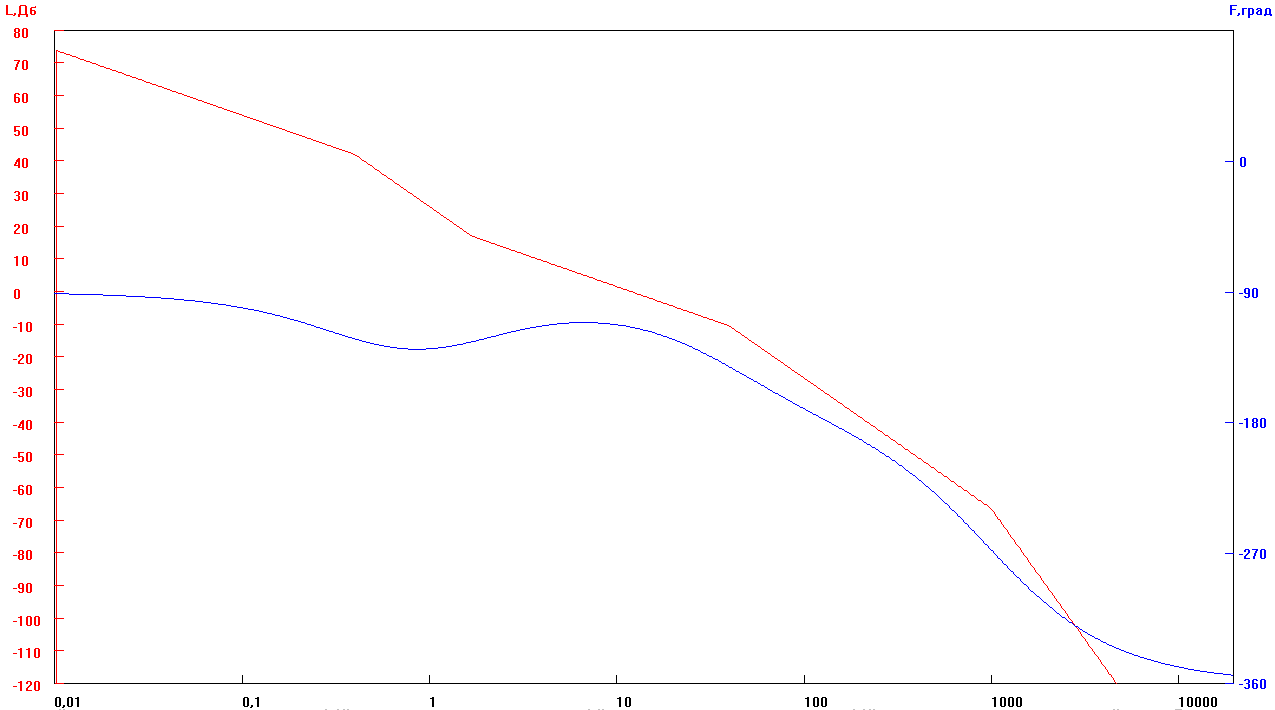
Рисунок 6 Логарифмическая амплитудно – частотная L(ω) и фазо – частотна φ(ω) характеристики скорректированной системы

Определим запас устойчивости скорректированной системы

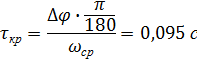
НЕЛИНЕЙНАЯ ЧАСТЬ

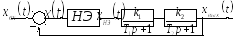
Рисунок 7 Структурная схема с нелинейным элементом

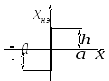
Рисунок 8 Статическая характеристика нелинейного элемента

(прямоугольный гистерезис)

Исходные данные: коэффициенты пропорциональности, постоянные времени и геометрические параметры характеристики нелинейного элемента