
- •Введение
- •1. Тематика курсовых работ
- •2. Объем и требования к оформлению курсовой работы
- •3. Примеры типовых заданий по курсовым работам
- •4. Некоторые особенности моделирования сау
- •4.1 Уравнения состояния непрерывных динамических систем
- •4.2 Особенности математического описания линейных дискретных систем
- •4.3 Математические модели дискретных (цифровых) сау
- •Список литературы
4. Некоторые особенности моделирования сау
4.1 Уравнения состояния непрерывных динамических систем
Уравнения состояния для динамического объекта, имеющего один входной сигнал u и один выходной сигналy, могут быть записаны в виде
![]() (4.1)
(4.1)
где
 , (4.2)
, (4.2)
а
![]() - транспонированный по отношению к
вектору
- транспонированный по отношению к
вектору![]() вектор.
вектор.
Отметим, что в (4.1) d=0, если порядок полинома числителя передаточной функции системы меньше порядка полинома знаменателя, т. е. коэффициент прямой передачи со входа на выход равен нулю.
Чаще всего в качестве переменных состояния принимается выходной сигнал и (n-1) его производных. Преимущества такого подхода – простота представления результатов. Кроме того, такое представление возможно для нелинейного дифференциального уравнения общего вида. Такая форма представления – нормальная форма или форма Коши.
В качестве примера представим в нормальной форме Коши линейный динамический элемент (объект управления), описываемый передаточной функцией:
![]() (4.3)
(4.3)
Здесь передаточная функция представлена в операторной форме; p=d/dt – оператор дифференцирования; для упрощения выражений примемa0=1.
В соответствии с нормальной формой переменные состояния будут
![]()
 (4.4)
(4.4)
Уравнения (4.4) можно записать в матричной форме (4.1), где
 (4.5)
(4.5)
Причём, a0=1.
Начальное состояние рассматриваемого динамического элемента определяется значением вектора x(0).
В случае, когда передаточная функция динамического элемента имеет более общий вид:
 (4.6)
(4.6)
матрица A имеет тот же вид (4.5), а матрица (вектор-столбец)bбудет
![]() (4.7)
(4.7)
где
![]() (4.8)
(4.8)
а выходной сигнал
![]() (4.9)
(4.9)
Таким образом, в (4.1) d=k0=b0.
В тех случаях, когда порядок полинома
числителя
![]() меньше порядка полинома знаменателя
получаем, как и раньше,
меньше порядка полинома знаменателя
получаем, как и раньше,
![]()
В общем случае для многомерных стационарных динамических систем (например, многосвязных объектов управления) уравнения состояния в нормальной форме Коши имеют вид
![]() (4.10)
(4.10)
Найдём связь между описанием в пространстве состояний и описанием в виде матричной передаточной функции многомерной динамической системы.
Обозначим через
![]() n-мерный вектор
состояния в области изображений Лапласа;
через
n-мерный вектор
состояния в области изображений Лапласа;
через![]() -r-мерный вектор
входных сигналов и
-r-мерный вектор
входных сигналов и![]() -m-мерный вектор
выходных координат рассматриваемой
системы. Соотношение между этими
векторами устанавливается передаточными
матрицами
-m-мерный вектор
выходных координат рассматриваемой
системы. Соотношение между этими
векторами устанавливается передаточными
матрицами![]() размера
размера![]() соответственно:
соответственно:
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
Откуда следует, что элемент
![]() матрицы
матрицы![]() представляет собой изображение по
Лапласу импульсной переходной функции
поi-й координате
состояния относительноj-го
входного сигнала при равенстве нулю
всех других входных сигналов.
представляет собой изображение по
Лапласу импульсной переходной функции
поi-й координате
состояния относительноj-го
входного сигнала при равенстве нулю
всех других входных сигналов.
При нулевых начальных условиях, применив к (4.10) преобразование Лапласа, получим
![]()
и далее
![]()
В соответствии с (3.32) и (3.33) получим
![]() (4.13)
(4.13)
![]() (4.14)
(4.14)
где
![]() - обратная матрица по отношению к матрице
- обратная матрица по отношению к матрице![]() .
.
4.2 Особенности математического описания линейных дискретных систем
В противоположность непрерывным сигналам, которые описываются непрерывными функциями времени, дискретные сигналы могут принимать лишь дискретные значения в дискретные моменты времени. Они представляют собой последовательности импульсов, появляющихся в определенные моменты времени. Обычно дискретный сигнал получается в результате периодического прерывания непрерывного сигнала с постоянным тактом.
Для получения разностного уравнения достаточно любую дискретную функцию, зависящую от другой дискретной функции, представить в рекуррентной форме. Линейное разностное уравнение порядка nимеет вид
![]() (4.15)
(4.15)
Здесь аргумент
![]() (
(![]() - такт квантования по времени) заменен
индексомk. Величину
выходного сигнала при любомkможно вычислить с помощью рекуррентной
формулы
- такт квантования по времени) заменен
индексомk. Величину
выходного сигнала при любомkможно вычислить с помощью рекуррентной
формулы
![]() (4.16)
(4.16)
если известны текущее значение входа
![]() и
и![]() предшествующих значений
предшествующих значений![]() ,
а также соответствующие значения выхода
–
,
а также соответствующие значения выхода
–![]() .
.
На основе (3.15) можно записать дискретную передаточную функцию, используя теорему z-преобразования о сдвиге вправо
![]()
 (4.17)
(4.17)
После подстановки в разностное уравнение (4.15) индексов, изменяющихся от kдо k+n, получим
![]() (4.18)
(4.18)
Последнее равносильно представлению (3.38) в виде
 (4.19)
(4.19)
Переход к описанию дискретной системы в пространстве состояний может осуществляться различными способами. Один из самых простых заключается в прямой подстановке переменных состояния в разностное уравнение (4.18):
![]() (4.20)
(4.20)
 (4.21)
(4.21)
Подставим выражение (4.21) в уравнение
(4.18), положив
![]()
![]() (4.22)
(4.22)
Это соотношение можно представить в форме векторного разностного уравнения
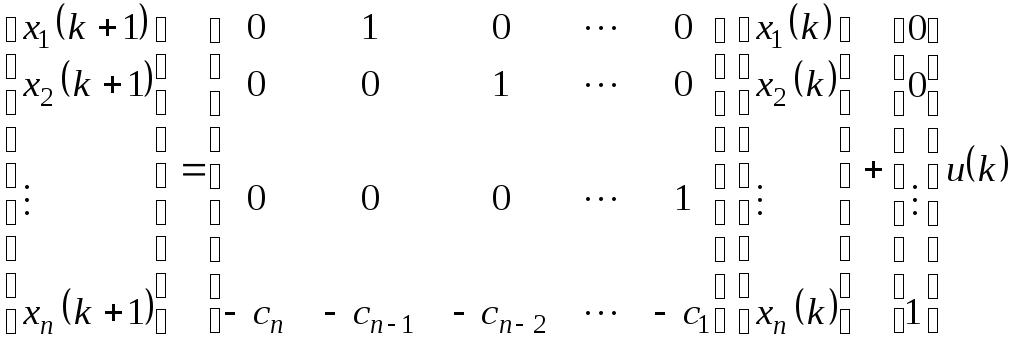
и уравнения выхода
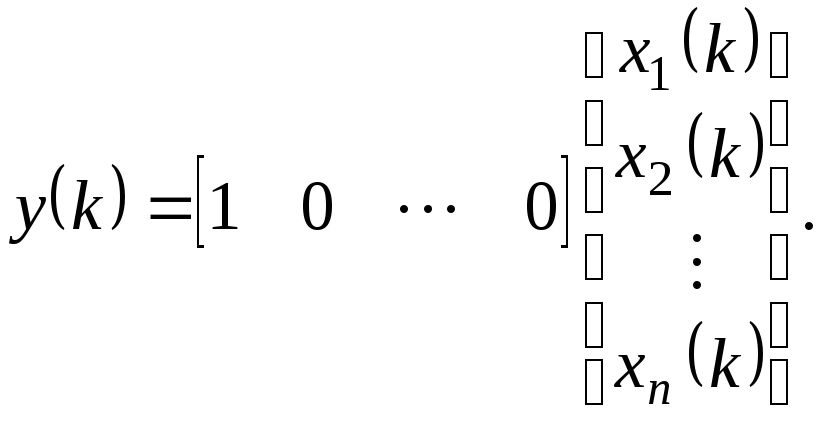
Обозначим вектор переменных состояния x, матрицу системыA, вектор передачи управления (входного сигнала)bи вектор наблюденияc:
![]() (4.23)
(4.23)
![]() (4.24)
(4.24)
Если
![]() то уравнения (4.19) и (4.20) можно представить
в форме
то уравнения (4.19) и (4.20) можно представить
в форме
![]() (4.25)
(4.25)
Если же
![]() уравнения (4.19) и (4.20) приводятся к виду
уравнения (4.19) и (4.20) приводятся к виду
![]()
или
![]() (4.26)
(4.26)
Кроме того, используя уравнение (4.21), можно получить выражение
![]() (4.27)
(4.27)
Определив
![]() из соотношения (4.22), получаем окончательный
результат
из соотношения (4.22), получаем окончательный
результат
![]() (4.28)
(4.28)
Это обобщённое уравнение выхода можно также записать в векторной форме:

или
![]() (4.29)
(4.29)
При
![]() =1,
т. е. для систем без прямой передачи
входного воздействия, уравнение (4.29)
приобретает вид
=1,
т. е. для систем без прямой передачи
входного воздействия, уравнение (4.29)
приобретает вид

Распространяя представление линейных дискретных систем с одним входом и одним выходом в пространстве состояний на линейные многомерные системы с r входамиu(k) иmвыходамиy(k), получим следующие матричные уравнения:
![]() (4.31)
(4.31)
![]() (4.32)
(4.32)
где x(k)
– вектор состояния размерности![]() - вектор управления (входов) размерности
- вектор управления (входов) размерности![]() ;y(k)– вектор выхода размерности
;y(k)– вектор выхода размерности![]() ;A – собственная
матрица системы размерности
;A – собственная
матрица системы размерности![]() ;B– матрица управления
размерности
;B– матрица управления
размерности![]() ;C – матрица выхода
(измерений) размерности
;C – матрица выхода
(измерений) размерности![]() ;D –матрица
входа/выхода (прямой передачи) размерности
;D –матрица
входа/выхода (прямой передачи) размерности![]() .
.
