3. Примеры типовых заданий по курсовым работам

Задание №1. «Идентификация и синтез САУ» (для 2 студентов)

Порядок выполнения работы:

1. Разработать алгоритм и программу вычисления параметров передаточной функции W(s) по экспериментальным характеристикам (метод Симою [1]). Передаточная функция имеет вид:

,

где K, b₁, a_i (i = 1,2,3) - неизвестные параметры.

2. Составить программу на ЭВМ для определения искомых параметров [1, 16]. Для проверки работоспособности и оценки помехоустойчивости алгоритма подготовить числовые данные, соответствующие объекту с передаточной функцией

При этом переходная характеристика h₀(t) определяется путём обратного преобразования Лапласа отW₀ (s)/s.

3. Рассмотреть 3 случая:

1. (точное значение переходной характеристики);

2. где- помеха с нулевым математическим ожиданием и интенсивностью 5% относительноk₀( в качествеиспользовать функцию случайных чиселRND);

3) где- помеха с интенсивностью 10% отk₀.

Структурная схема САУ (рис.3.1):

W_ку(s)

H_нс(t)

W_д(s)

КУ НС

g(t) e(t) u(t) (t) x(t)

• Д

Рис.3.1

- передаточная функция датчика;

полученная “экспериментально” переход- ная характеристика нескорректированной системы (объекта управления) с учётом помех(t).

Требуется ( в соответствии с вариантом задания (таблица 3.1)):

1. определить

используя программу, разработанную в п.1;

2) определить в результате синтеза передаточную функцию корректирующего устройства W_КУ(s), обеспечив при этом заданные требования к САУ: время регулирования (t_рег.); перерегулирование_x; установивщуюся ошибкуe_уст.;

3) найти передаточную функцию замкнутой САУ Ф(s), записать дифференциальное уравнение замкнутой САУ в нормальной форме Коши;

4) составить программу расчёта переходного процесса замкнутой САУ на ЭВМ;

5) построить переходный процесс по координатам x(t),u(t) приg(t)=1(t).

Таблица 3.1

№ вар	W0(s)					WД(s)								tрег	x	eуст
	K0	T1	T2	T3	T4	KД	TД	K	1	2	1	2	
1	1	1	0,5	0,33	0,25	0,1	0,05	0,5	-0,75	0,25	2,5	5	0,03	2	10	0
2	3	0,5	0,33	0,25	0,2	0,2	0,1	0,1	-0,15	0,05	2	5	0,008	2,5	5	0
3	2	2	1	0,5	0,33	0,3	0,05	0,05	-0,0 75	0,025	2	3,3	0,003	1,5	10	0
4	2	1	0,4	0,3	0,3	0,15	0,15	0,15	-0,2 25	0,075	1,5	4	0,01	2	7	0
5	2,5	1	1	0,4	0,1	0,25	0,03	0,3	-0,45	0,15	2,5	3	0,02	1,5	4	0
6	4	3	2	1	0,5	1	0,1	1	-1,5	0,5	3	4,5	0,07	2	10	0

Постоянные времени и время регулирования в таблице 3.1 даны в секундах, остальные параметры – безразмерны.

Литература [1, 10, 16]

Задание № 2«Синтез формирующих фильтров и анализ САУ при стационарных случайных воздействиях» (для 2 студентов)

Синтезировать формирующий фильтр (ФФ), позволяющий получить стационарный случайный сигнал с корреляционной функцией [4, 13]:

и спектральной плотностью

из исходного сигнала типа "белого шума" n(t). В качестве последнего рекомендуется использовать функцию случайных чиселRND(с нулевым математическим ожиданием);

Определить передаточную функцию формирующего фильтра W_фф(s).

Для структурной схемы САУ (рис. 3.2):

n(t)

W_фф(s)

W_ку(s)

W_им(s)

W_оу(s)

g(t) e(t) u(t)(t)

-x(t)

Рис. 3.2

1) определить параметры регулятора

при которых обеспечиваются заданные показатели качества САУ:

t_рег; перерегулирование_x(при(t)=0);

2) составить программу моделирования переходных процессов в САУ с помощью РС и построить переходный процесс при g(t)=1(t) (при(t)=0);

3) составить программу и определить корреляционную функцию сигнала (t), сопоставить её с заданной корреляционной функциейR_(). При определении корреляционной функции рассматривать установившуюся реакцию(t) на выходе ФФ, т.е. через (4-5) постоянных времениW_фф(s);

4) определить математическое ожидание, дисперсию и дифференциаль- ный закон распределения сигнала (t);

5) определить среднеквадратичное значение сигнала x(t) приg(t)=0,

n(t) - "белый шум" (см. рис. 3.2).

Таблица 3.2

№ вар		0 [1/c]	x [%]	tрег [c]
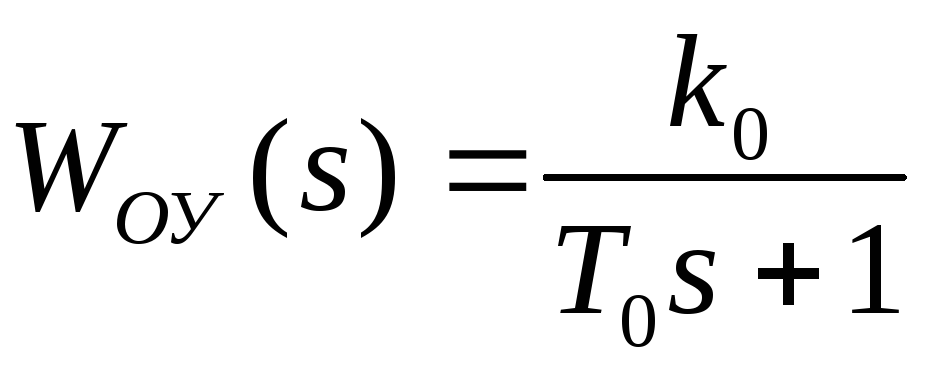
					k0	T0 [c]	kИМ	TИМ [c]
1	0,10	12	10	1,5	2,0	0,5	0,15	0,1
2	0,05	6	10	1,5	1,0	0,3	0,20	0,5
3	0,10	3	15	1,5	0,5	0,2	0,30	0,4
4	0,15	8	15	1,5	3,0	0,4	0,40	0,2

Литература [4 - 6, 15]

Задание № 3.«Синтез оптимальных параметров САУ»

Структурная схема САУ имеет вид (Рис. 3.3).

W_ку(s)

W_им(s)

W_оу(s)

g(t) e(t) u(t) x(t)

- –

W_д(s)

x₁(t)

Рис. 3.3

Передаточные функции объекта управления (ОУ), исполнительного механизма (ИМ), датчика (Д) и корректирующего устройства (КУ):

Порядок выполнения задания:

1. Найти передаточную функцию замкнутой САУ по ошибке. Записать дифференциальное уравнение замкнутой САУ, связывающее координаты g(t) и ε(t);

2. Привести дифференциальное уравнение САУ к нормальной форме Коши, составить программу моделирования переходных процессов в САУ с помощью ЭВМ.

3. Предусмотреть в программе возможность вычисления интегральной квадратичной оценки

4. пользуясь симплексным методом оптимизации [7], найти оптимальные значения параметров k и Tкорректирующего устройства из условия:

5. построить переходный процесс в САУ при найденных оптимальных значениях параметров k и T;

6. построить зависимость полагая

Литература [3, 7, 14,18]

Задание № 4.«Синтез непрерывного регулятора».

Структурная схема САУ и исходные данные соответствуют рис. 3.3.

1. Найти передаточную функцию замкнутой САУ, записать дифференциальное уравнение замкнутой САУ;

2. Привести дифференциальное уравнение САУ к нормальной форме Коши, составить программу моделирования переходных процессов в САУ с помощью ЭВМ;

3. Построить переходные процессы по координатам

4. Разработать алгоритм для определения оптимальных параметров корректирующего устройства , исходя из следующих требований:

5. где - соответственно, перерегулирования по координатам

6. воспользовавшись разработанным алгоритмом, выбрать оптимальные (допустимые) значения параметров КУ – k иT.Построить соответствующие им переходные процессы по координатам

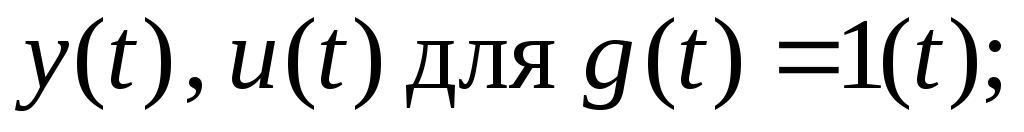
7. предложить алгоритм для построения на плоскости параметров (k, T)допустимой области, обеспечивающей выполнение предъявленных к САУ требований.

Литература [3-5, 13-14, 18]

Задание №5.Синтез цифровой САУ

Структурная схема САУ имеет вид (рис. 3.4).

КУ ФЭ НС

R(z)

g(t) ε(t) u(t) x(t)

–

Рис. 3.4

Порядок выполнения задания:

1. выбрать частоту дискретизации f₀=1/T₀ cучетом динамических свойств нескорректированной системы НС и требований к САУ (t_рег ≈ 2с);

2. найти дискретную передаточную функцию W(z) для приведенной непрерывной части САУ, дать эквивалентную структурную схему импульсной САУ;

3. найти структуру и параметры КУ, обеспечивающие решение задачи синтеза;

4. определить дискретную передаточную функцию замкнутой САУ, записать разностное уравнение замкнутой САУ;

5. разработать программу моделирования переходных процессов в импульсной САУ;

6. построить переходный процесс в САУ при синтезированных значениях параметров КУ, полагая g(t) = 1[t].

Литература [9, 12, 14, 16]

Задание № 6.«Цифровая САУ»

Передаточная функция нескорректированной системы НС:

.

Передаточная функция регулятора – аналогового прототипа:

.

Период дискретизации T=0,1 c.

Порядок выполнения задания:

1. найти дискретную передаточную функцию (ДПФ) приведенной непрерывной части W(z);

2. используя преобразование Тастина , найти ДПФ цифрового регулятораR(z);

3. получить разностное уравнение замкнутой САУ;

4. построить переходный процесс x[n] на выходе САУ дляg[n]=1[n].

5. построить переходный процесс x[n],вводя сбой (кратковременное импульсное изменение) по переменнойu[n];

6. предложить алгоритм «парирования» сбоя, используя в цифровом вычислителе (регуляторе) квадратичную экстраполяцию управляющего воздействия:

7. сделать соответствующие выводы по результатам моделирования.

Литература [9, 12, 14, 16]

Задание № 7«Цифровая система автоматического регулирования»

Исходные данные:

Передаточная функция нескорректированной системы НС:

передаточная функция регулятора – аналогового прототипа:

Порядок выполнения задания:

1. найти дискретную передаточную функцию (ДПФ) приведенной непрерывной части W(z), полагаяT=0,05c;

2. используя преобразование Тастина , найти ДПФ цифрового регулятораR(z);

3. составить разностное уравнение замкнутой САУ;

4. построить переходный процесс x[n] на выходе САУ дляg[n]=1[n];

5. повторить пп. 1–4, полагая T=0,25 c. При моделировании переходного процессаx[n] сохранить шаг интегрирования

6. определить показатели качества САУ для каждого из рассмотренных выше двух случаев. Сделать соответствующие выводы по результатам моделирования.

Литература [9, 12, 14, 16]

Задание № 8«Синтез цифровых САУ методом аналогового прототипа»

Структурная схема непрерывной САУ (Рис. 3.5:

W_ку(s)

W_им(s)

W_оу(s)

g(t) e(t) u(t) x(t)

- –

Рис. 3.5

Здесь

Порядок выполнения задания:

1. Методом ЛАХ синтезировать САУ с заданными параметрами: t_рег; σ (см. таблицу 3.3);

2. Разработать программу моделирования переходных процессов в САУ с помощью ЭВМ;

3. Построить переходный процесс по координате x(t) дляg(t)=1(t);

4. Используя 3 способа дискретизации непрерывного регулятора, полученного в процесс синтеза, исследовать соответствующую цифровую САУ:

1. – преобразование Тастина:

2. – преобразование методом прямоугольников:

3. – стандартное z-преобразование:

гдеZ{…} – символz-преобразования.

5. В процессе исследования определить максимальный период дискретиза- ции цифровой САУ T₀, при котором удовлетворяются заданные требования к САУ; построить переходные процессы по координатеx(t) дляg(t)=1(t).

6. Сделать выводы, сопоставив результаты, полученные в процессе указанных способов преобразования (1 – 3).

Таблица 3.3

№ варианта	Wоу(s)		Wим(s)		tрег [c]	σ [%]
	k0	T0	kим	Tим
1	2	0,5	0,15	0,1	2,0	20
2	1	0,4	0,30	0,3	2,5	15
3	0,5	0,2	0,10	0,1	1,0	10
4	4,0	0,7	0,25	0,4	2,0	5

Литература [9, 12, 14, 16]

Задание № 9.«Цифровой фильтр низких частот»

Передаточная функция аналогового фильтра низких частот:

(3.1)

Порядок выполнения задания:

1. составить программу реализации цифровых фильтров низких частот W_ф[z]на ЭВМ, используя указанные взадании №8способы дискретизации аналогового фильтра (3.1);

2. выбрать период дискретизации T₀;

3. оценить эффективность полученных цифровых фильтров с помощью вычислительного эксперимента на ЭВМ:

полезный сигнал–;

помеха: а) – функция случайных чиселRND(0) с нулевым математи- ческим ожиданием и интенсивностьюη [%] относительно полезного сигнала;

б) – функция случайных чисел RND(0) с нулевым математическим ожиданием и интенсивностьюη [%] относительно полезного сигнала, «пропущенный» через формирующий фильтр с передаточной функцией (рис. 3.6):

W_ф[z]

x[n] y[n]

η[n]

Рис. 3.6

4. сделать выводы, сопоставив результаты, полученные в процессе указанных способов преобразования (1 – 3).

Таблица 3.4

№ варианта	Tф [c]	Tфф [c]	η [%]
1	0,15	0,05	5
2	0,05	0.02	8
3	0.10	0,035	6

Литература [9, 12, 14, 16]

Задание № 10.«Цифровой сглаживающий фильтр»

Расчетные формулы для цифровых сглаживающих фильтров:

- для сглаженной функции:

- для производной входной функции:

где N=3.

Порядок выполнения задания:

1. Разработать программы для реализации данных формул на ЭВМ;

2. Проверить программы путем вычислений на тестовом примере (рис. 3.7):

η(t)

n(t) x(t)

Цифровой

фильтр

Рис. 3.7

Здесь – полезный сигнал;

– фоновая помеха (аддитивная, нормально распределенная, центрированная);

3. сопоставить

4. разработать алгоритм и составить программу цифрового фильтра при наличии не только фоновых, но и импульсных помех см. рис. 3.8 (где t₁ и t₂ – моменты воздействия импульсных помех);

x(t),

x(t)

t

t₁ t₂

t

Рис. 3.8

сформулировать соответствующие выводы относительно эффективности использования цифровых фильтров.

Литература [9, 12, 14, 16

]

Задание № 11. «Синтез многосвязной САУ»

Структурная схема двусвязной САУ имеет вид (рис. 3.9):

g₁ - ε₁ u₁ x₁

g₂ ε₂ u₂ x₂

-

R₁(s)

W₁₁

W₁₂

W₂₁

W₂₂

R₁(s)

Рис. 3.9

Уравнения объекта управления:

Уравнение регулятора:

Выполнить следующие действия:

1. найти передаточную матрицу замкнутой МСАУ, записать характеристическое уравнение системы;

2. исходя из заданных требований выбрать желаемый характеристический полиномзамкнутой МСАУ;

3. определить параметры многомерного регулятора из условия

4. разработать программу моделирования переходных процессов в замкнутой МСАУ, предусмотрев в ней возможность изменения параметров

5. построить переходные процессы в синтезированной МСАУ по координатам для следующих случаев:

а) g₁(t)=1(t), g₂(t)=0;

б) g₁(t)=0, g₂(t)=1(t).

6. Определить показатели качества t_рег иσ по каждой из координат;

7. предложить алгоритм диалоговой оптимизации параметров регулятора k₁, k₂, обеспечивающей выполнение поставленных требований.

В качестве критерия оптимальности можно использовать критерий:

где – соответственно, величина перерегулирования и времени регулирования по координатеx_i(t) при единичном ступенчатом воздействииg_i(t);t^*=(2…3)c.

Литература [7, 12, 14]

Задание № 12. «МСАУ»

Произвести синтез параметров МСАУ :

– уравнения многосвязного объекта управления:

– уравнения регулятора:

Порядок выполнения задания:

1. Привести уравнения замкнутой МСАУ к нормальной форме Коши;

2. Разработать программу моделирования переходных процессов в замкнутой МСАУ и вычисления функционала I= I₁+I₂,

где

3. Принять g(t)=1(t); T_k=5 c; шаг интегрирования

4. Найти оптимальные параметры k₁, k₂ регулятора, обеспечивающие выполнение условияВоспользоваться симплексным методом поиска [7];

5. Построить переходные процессы x₁(t), x₂(t)в замкнутой САУ для оптимальных значений параметровk₁, k₂;

6. Определить показатели качества синтезированной МСАУ.

Литература [7, 12, 14]

Задание № 13. «Синтез нелинейной САУ»

Структурная схема САУ (рис. 3.10):

ОУ

КУ НЭ1

g ε v u x

- НЭ2

y

R(s)

Рис. 3.10

Характеристики нелинейных элементов (НЭ) имеют вид:

Требования к САУ: порядок астатизма ν=1, время регулирования t_рег≈3-4 с, перерегулированиеσ≤20%.

Выполнить следующие действия:

1. выбрать желаемую передаточную функцию Ф^*(s) замкнутой системы;

2. найти передаточную функцию корректирующего устройства R(s)

3. исходя из заданных требований к системе;

4. произвести математическое моделирование переходных процессов в САУ по координатам x(t), y(t) для g(t)=1(t);

5. повторить п. 3 для следующих случаев:

а) g(t)=0,5 1(t); б)g(t)=2 1(t).

6. Объяснить полученные результаты, определить диапазон регулирования и максимальное время регулирования по координате x(t);

7. составить программу вычислений с помощью ЭВМ интегральных квадратичных оценок

8. где x(t) – реакция САУ наg(t)= 1(t);x^*(t) – реакция эталонной САУ с передаточной функциейФ^*(s); T – время расчета,

9. показать соответствуют или нет расчетные значения параметров КУ минимуму интегральной квадратичной оценки I₁ и I₂.

Литература [3, 5, 18, 19]

Задание № 14.«Синтез двухконтурной САУ»

Структурная схема САУ имеет вид (Рис.3.11):

КУ ИМ ОУ

K₂

g(t) ε(t) u(t) x(t)

• -

Рис. 3.11

Выполнить следующие действия:

1. определить передаточную функцию замкнутой САУ;

2. определить устойчивость замкнутой САУ при различных параметрах ОУ, если 0,5≤K₀≤5,0; 0,5≤T₀≤3,0. ПринятьK₁=K₂=1; T₁=2,0;

3. разработать программу моделирования САУ на ЭВМ при различных значениях параметров K₁ ,K₂ ,K₀ ,T₀;

4. произвести синтез параметров КУ в соответствии с предложенным алгоритмом.

Требования, предъявляемые к САУ:

• передаточная функция системы Ф(s)должна совпадать желаемой передаточной функциейФ^*(s) в заданных точкахs_i на вещественной оси (s_i>0):

Ф(s_i) = Ф^*(s_i), I=1, 2, …, n. (3.2)

• Желаемая передаточная функция:

• Для ОУ принять K₀ =2, T₀=1.

• Дополнительное движение Δx(t) в системе не должно превышать заданной величиныmax│Δx_j(t)│≤0,15.

Здесь Δx_j(t)= x_j(t) – x^*(t);

x_j(t) – переходная функция САУ на одном из режимов работы ОУ;

x^*(t) – переходная функция эталонной системы сФ^*(s).

Рассматриваются следующие режимы работы ОУ:

№ 1 – K₀ =5, T₀=3;

№ 2 – K₀ =0,5, T₀=0,5;

№ 3 – K₀ =5, T₀=0,5.

Примечания:

• При решении уравнения (2) воспользоваться методом наименьших квадратов.

• В пояснительной записке привести график max│Δx_j(t)│=F(K₂).

• Блок-схема алгоритма синтеза:

Задать начальные значения K₂= (K₂)_min

Вычислить K₁ иT₁

из условия (3.1)

Моделирование САУ на режимах 1, 2, 3

K₂= K₂+ΔK₂

Останов

Да

Нет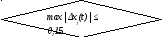

Рис. 3.12

Литература [3, 5,12, 14]