0. Построение желаемой лачх системы

Построим желаемую ЛАЧХ системы в разомкнутом состоянии в

соответствии с требованием обеспечения перерегулирования  по

задающему воздействию не более 30 % . Для этого необходим запас

по фазе 45 и по амплитуде L0,75 лог (рис.4). Это должно

соответствовать фазе _p^жел(_с)135. Примем частоты сопряжения

участков с наклоном –1 лог/дек и –2 лог/дек, равной _d, участков с

наклоном –2 лог/дек и –3 лог/дек, равной _ф, и частоту сопряжения ₄

участков с наклонами –3 лог/дек, чтобы она не влияла на запас

устойчивости  и L, т.е. ₄>10₀. Для такой конфигурации L_Р^ЖЕЛ()

(см. рис. ). L определяется координатами L_Р^ЖЕЛ при абсциссе, лежащей

на середине отрезка между lg_d и lg_ф, т.е. должно соблюдаться условие

(или ).

Частота среза желаемой ЛАЧХ разомкнутой системы принимается

наименьшему из значений, рассчитанных по приведённым

формулам: ; . Тогда

Выбираем lg _С=0,95 (_С=10^0,95=8,91 с^-1).

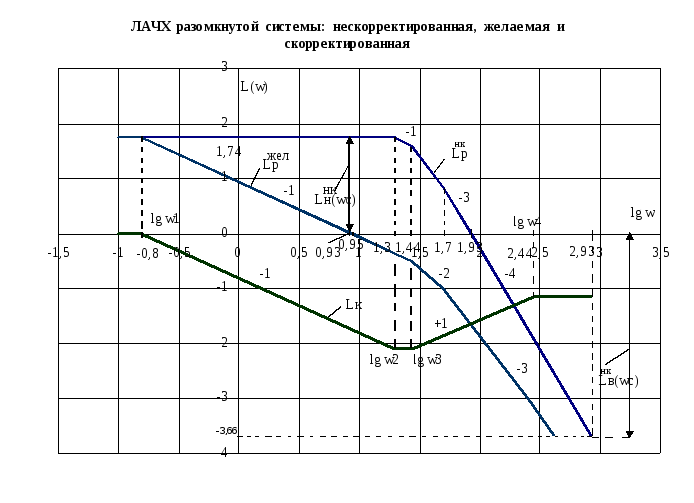
По приведенной выше методике определена частота _С и построена

желаемая ЛАЧХ L_Р^ЖЕЛ().

Динамическая составляющая ЛАЧХ L_К^!() корректирующего устройства

(коэффициент К_I учтен в К_{Р МАКС}) получается путем вычитания

зависимости L_Р^НК() из L_Р^ЖЕЛ(), т.е.

Полная ЛАЧХ корректирующего устройства

L_К()=lg К₁ + L_К^!().

Построим ЛАЧХ корректирующего устройства.

В качестве реализации схемотехники выберем операционный

усилитель, включённый по схеме, рис.5.

Передаточная функция будет иметь вид:

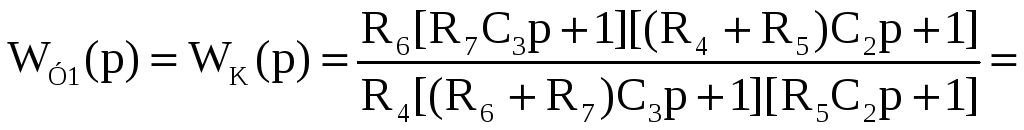
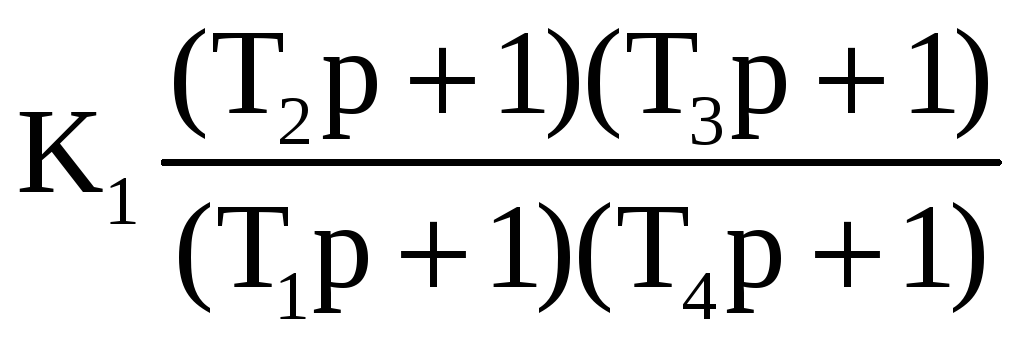
Данному случаю соответствует комбинированная коррекция, при

T₁>T₂>T₃>T₄.

По полученному выражению передаточной функции составим

Рис.4

систему из пяти уравнений для нахождения неизвестных

параметров корректирующего устройства. Примем значение

, а остальные параметры получим из решения системы

уравнений.

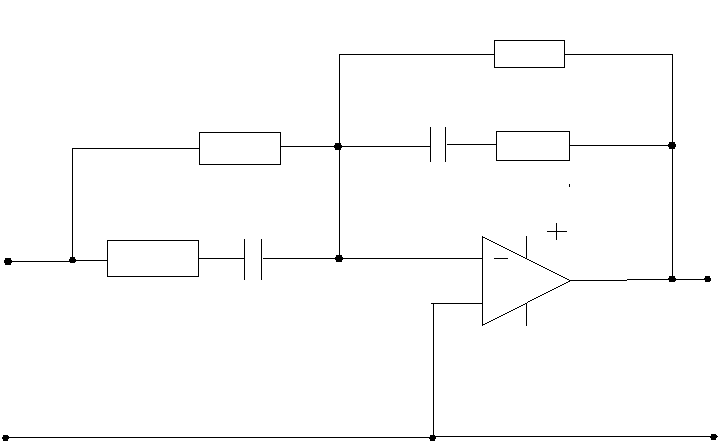
Рис.5

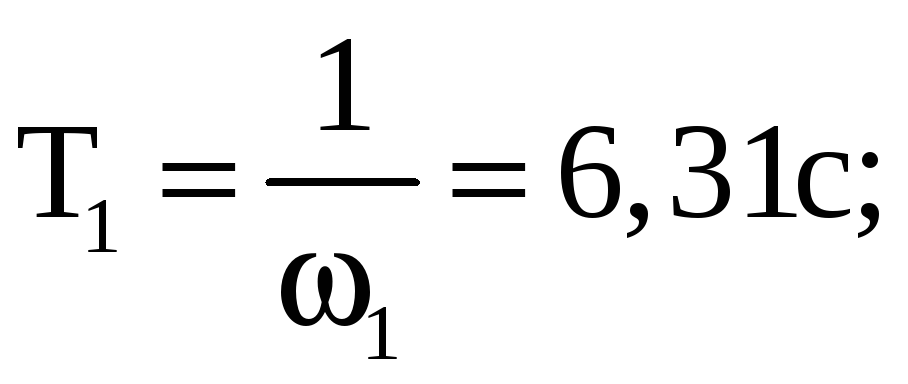
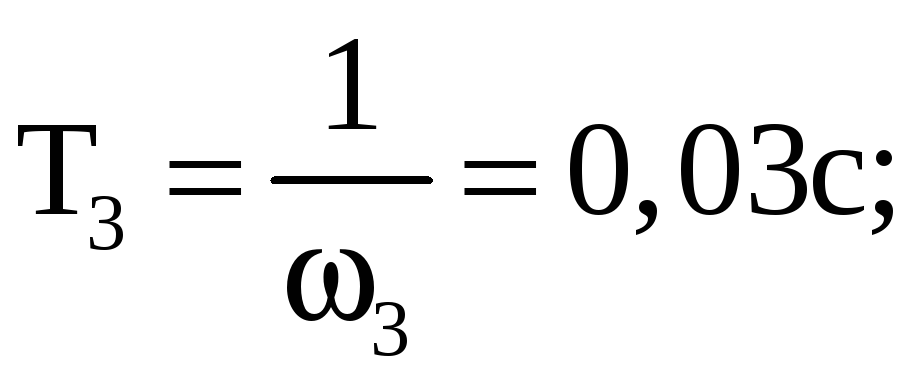
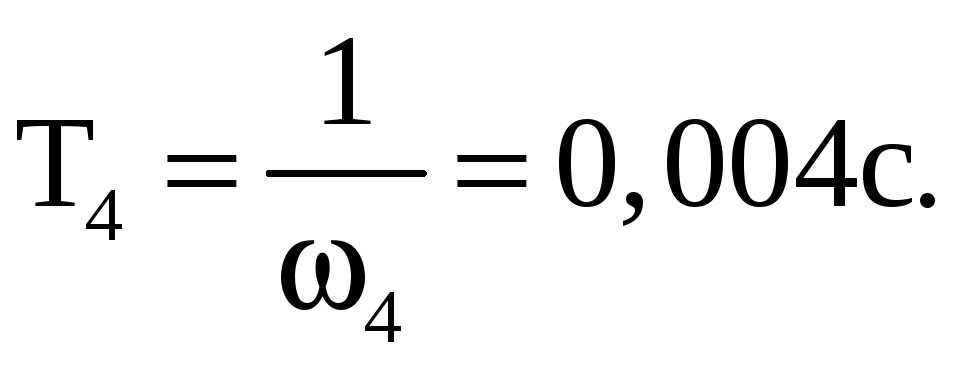
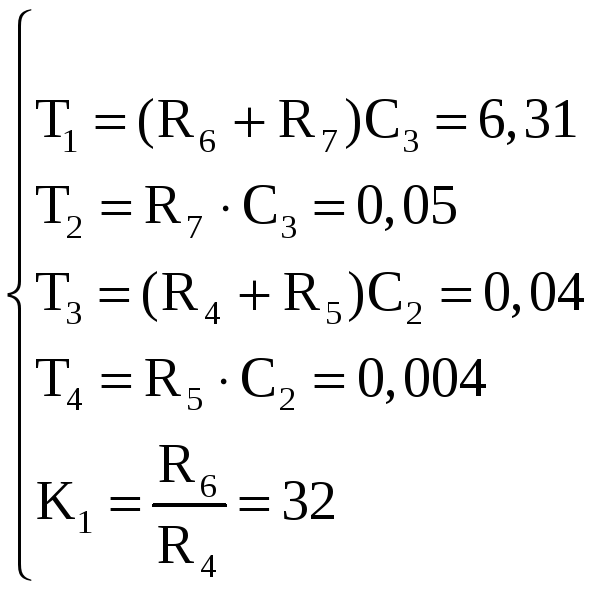
Из полученной системы уравнений находим:

Ом Ом ;

Ом

Найдём передаточную функцию скорректированной

разомкнутой системы:

.

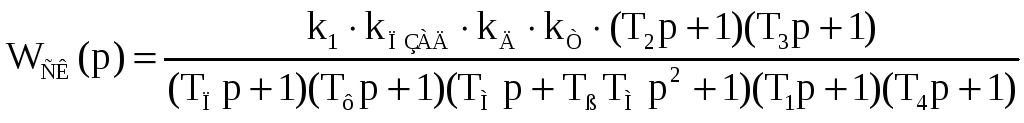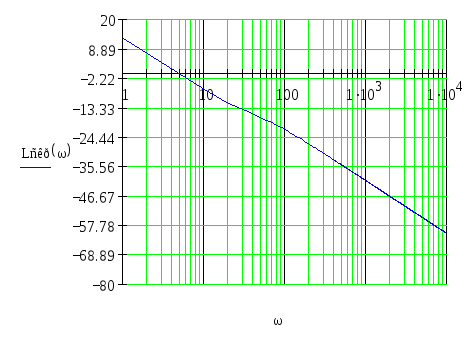
ЛАЧХ скорректированной разомкнутой системы имеет вид(в

децибелах):

График на рис.6:

Рис.6

Желаемая ЛАЧХ передаточной функции

разомкнутой системы имеет вид (в децибелах):

.

Найдём логарифмическую АЧХ прямого канала

скорректированной системы:

–

Логарифмическая АЧХ обратного канала:

Обратная ЛАЧХ канала обратной связи:

Найдём фазочастотную характеристику прямого канала

скорректированной САУ:

–

;

По полученным выражениям построим графики ЛАЧХ.

Преобразуем структурную схему к виду, удобному для

построения ЛЧХ по отношению к управляющему воздействию

и основным возмущающим воздействиям :

Рис. 7

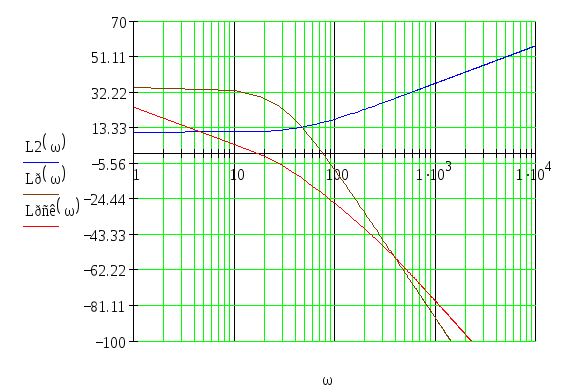
Рис.8 Преобразованная структурная схема схема САУ

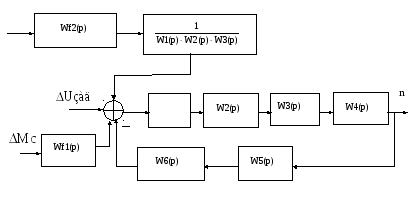
Передаточная функция замкнутой системы по отношению к

задающему воздействию при равенстве нулю возмущающих

воздействий имеет вид:

.

Передаточная функция замкнутой системы по возмущающему

воздействию(колебанию напряжения сети ) равна:

Точная ЛАЧХ замкнутой скорректированной системы будет

иметь вид(рис.9):

Рис.9

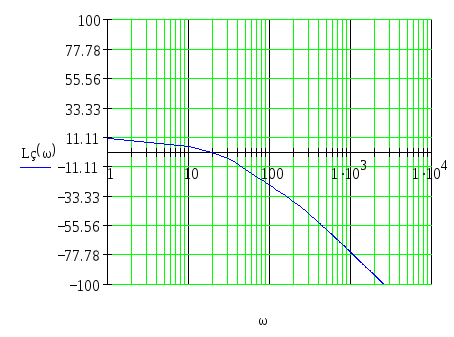
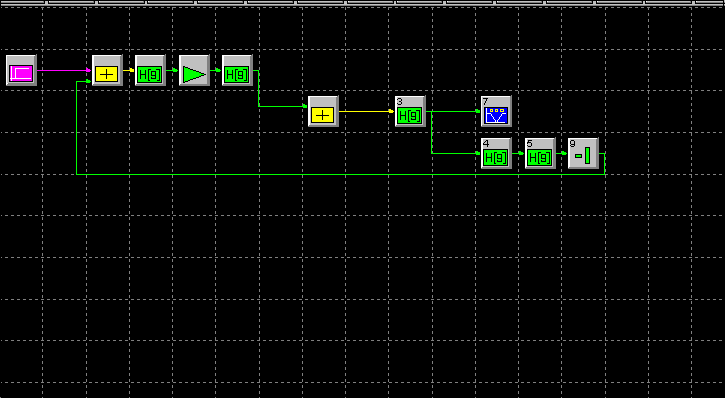
Построим точные ЛАЧХ САУ моделированием, для этого

Используем непреобразованную структурную схему,

записанную в программе Sistem View, рис. 10.

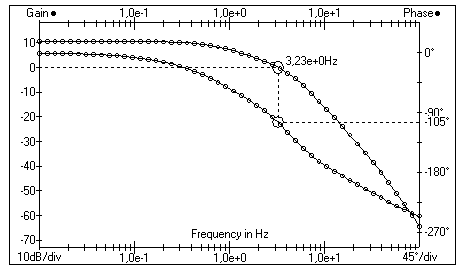
Согласно графикам рис.10 замкнутая скорректированная система

является устойчивой, так как частота среза ЛАЧХ меньше частоты,

при которой ЛФЧХ пересекает линию фазы

Коэффициент скорректированной разомкнутой системы равен:

Согласно графика максимум модуля частотной характеристики равен:

.

Значение АЧХ при равно:

; .

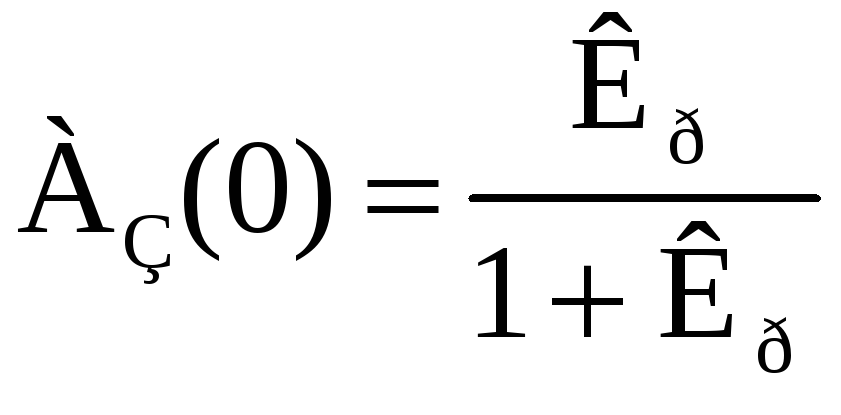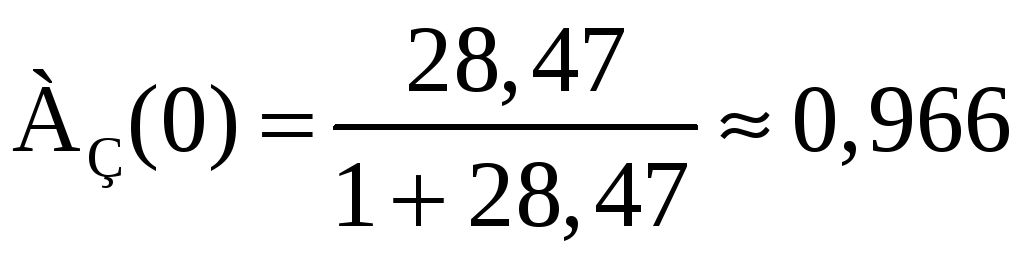Рис.10

Показатель колебательности M равен:

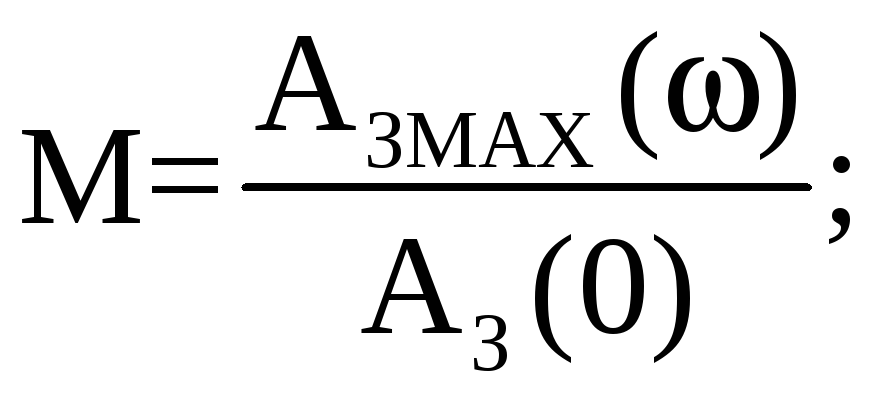
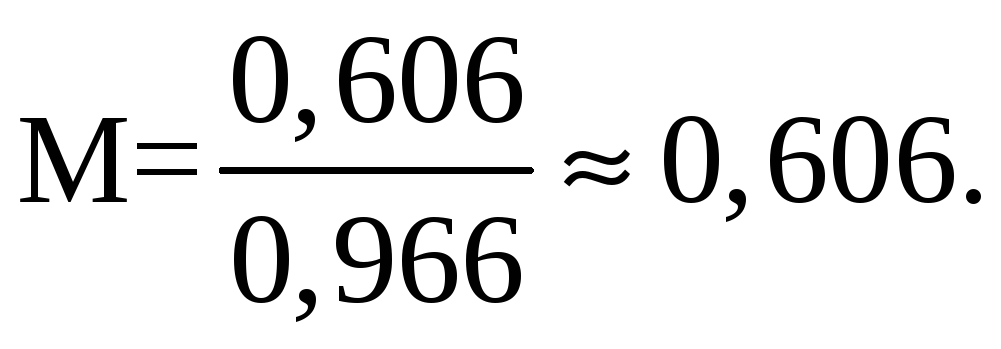
Показатель колебательности является удовлетворительным, так как не

превышает 1,5 для нормально работающих систем.

Рис.11

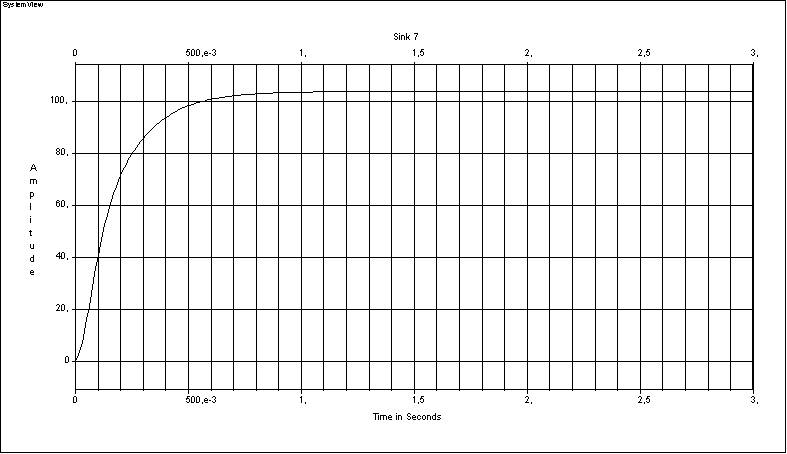
Время регулирования является временем переходного процесса системы,

в данном случае практически принимают равным 3Т.

Переходная характеристика Рис. 11

Из рис.11. время регулирования равно:

Перерегулирование в данном случае практически равно нулю.

Рис.12

При отсутствии задающего воздействия и наличии возмущающего

воздействия график переходной функции имеет вид, рис 14.

Наличие всплеска говорит о незначительном затухающем

колебании в системе, которое при подаче задающего воздействия

не влияет на работу системы и вид переходной характеристики будет

как на рис. 11 и рис.12.

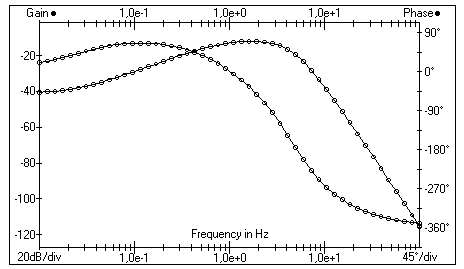
На рис.15 показана ЛАЧХ при возмущающем воздействии, которая

принимает отрицательные значения на всём диапазоне частот. Система

остаётся устойчивой.

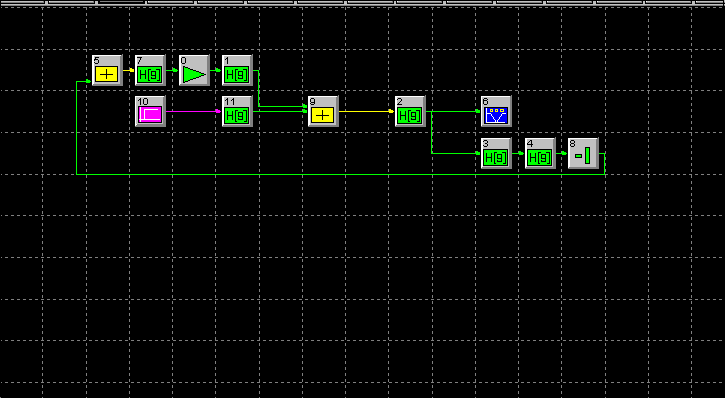
Рис.13

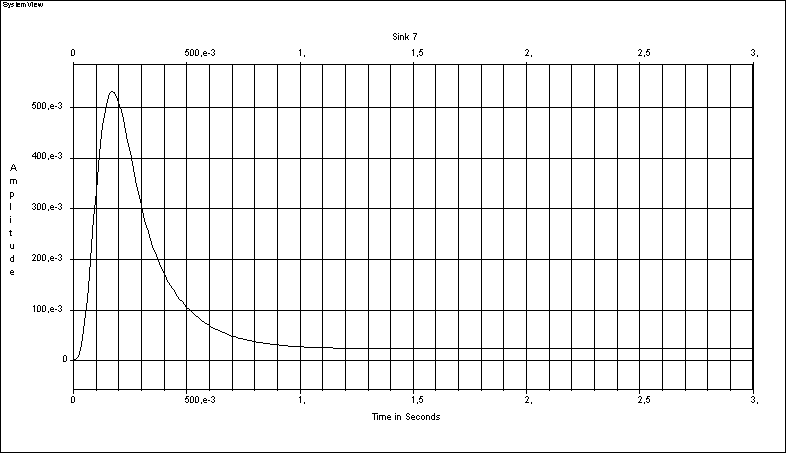
Рис.14

Рис.15

Библиография:

1. Теория автоматического управления: Учебник для вузов /Под ред.

А.В. Нетушила. – 2-е изд. – М.: Высш. шк., 1976. – 400 с.

2. Куропаткин П.В. Теория автоматического управления: Учеб. пособие.

– М.: Высш. шк., 1973. – 527 с.

3. Солодовников В.В. Основы теории и элементы систем

автоматического регулирования: Учеб. пособие. – М.: Машиностроение,

1985. – 536 с.

4. Теория автоматического управления /Под ред. А.А.Воронова. Ч. 1. –

М.: Высш. шк., 1977.