20. Геометрический смысл смешанного произведения

Построим параллелепипед на векторах , , с общим началом, как на ребрах. Пусть вектор

Тогда =, где для правой тройки векторов , , , для левой, наоборот,.

Таким образом, =, (8.17)

где V – объем параллелепипеда, образованного векторами , , .

Смешанное произведение векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Отсюда,

, (8.18)

, (8.19)

. (8.20)

21. Смешанное произведение в ортонормированном базисе

Даны векторы , , ,

т.е. , ,

Вычислим смешанное произведение

=()()==

===

==.

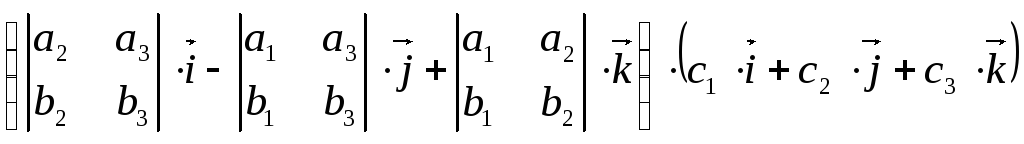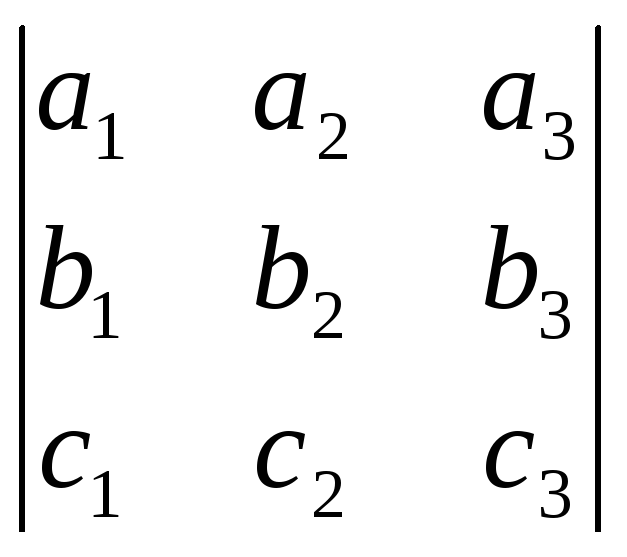. (8.21)

Пример 5.

Вычислим объем тетраэдра DАВС: А(1;2;1), В(4;1;2), С(1;5;3), D(2;3;1).

Решение. .

Найдем координаты ,, , на которых построен тетраэдр DАВС, как на ребрах: (3;–1;1), (0;3;2), (1;1;0).

Вычислим смешанное произведение и объем тетраэдра:

Приложения произведений векторов

п/п	Вид операции	Приложение
1	Линейная	Условие коллинеарности
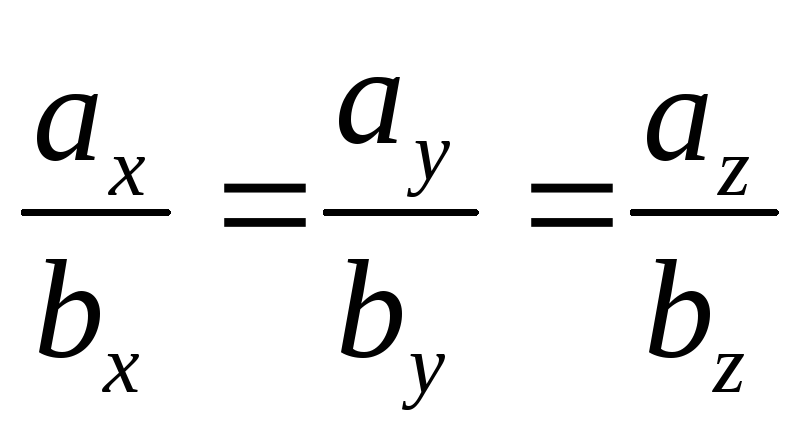
2	Скалярное произведение	Условие перпендикулярности векторов: Если , то векторы перпендикулярны
3	Скалярное произведение	Вычисление угла между векторами
4	Векторное произведение	Условие коллинеарности векторов: =.
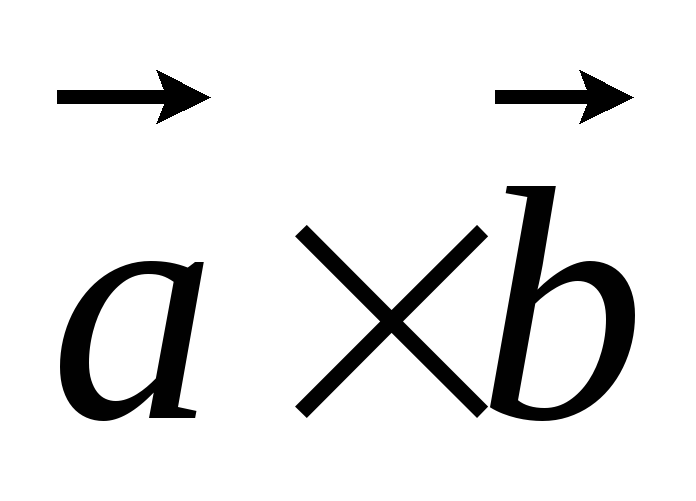5	Векторное произведение	Вычисление площади параллелограммов и треугольников, построенных на векторах с общим началом как на сторонах и
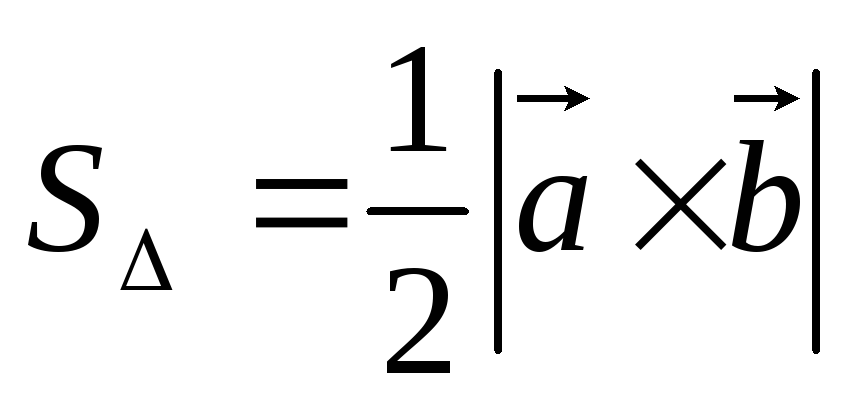
6	Векторное произведение	Момент силы
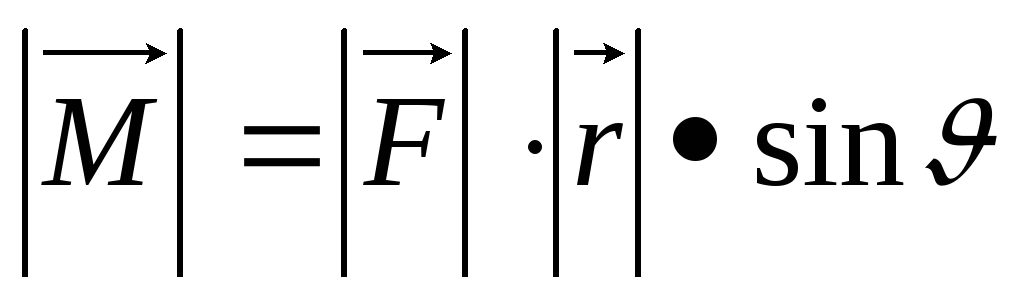
7	Смешанное произведение	Вычисление объема параллелепипеда, четырехугольной пирамиды, тетраэдра (треугольной пирамиды), построенных на трех векторах с общим началом, как на ребрах: , ,
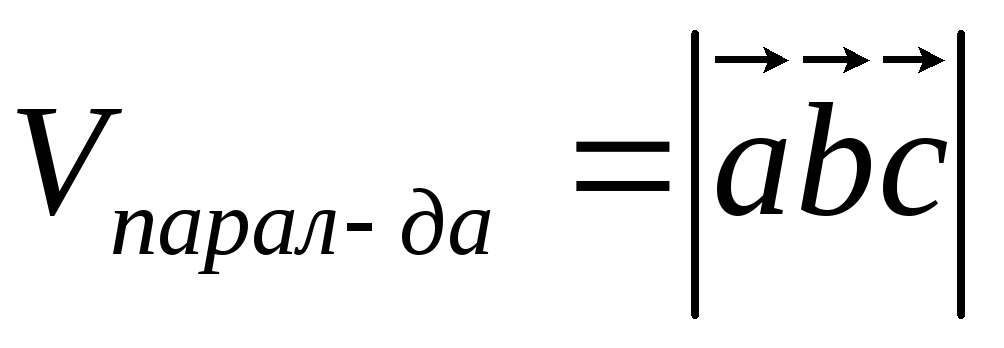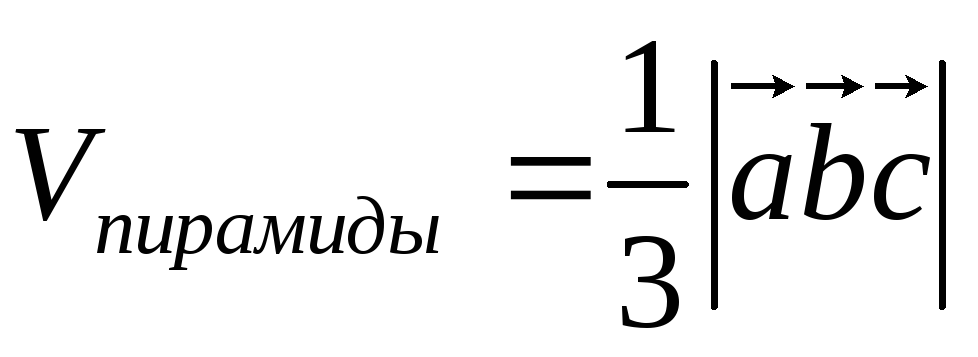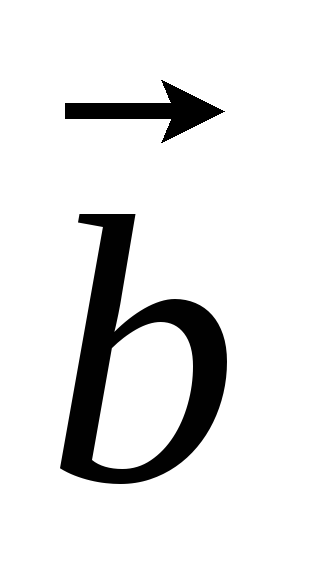
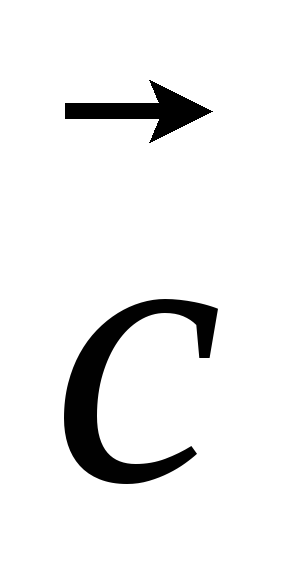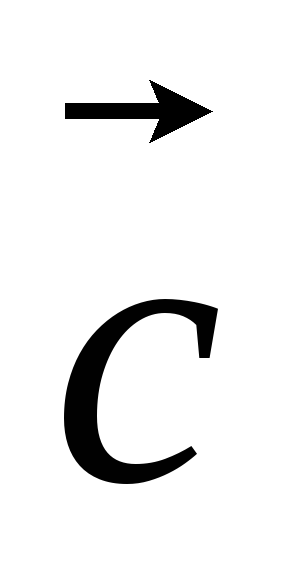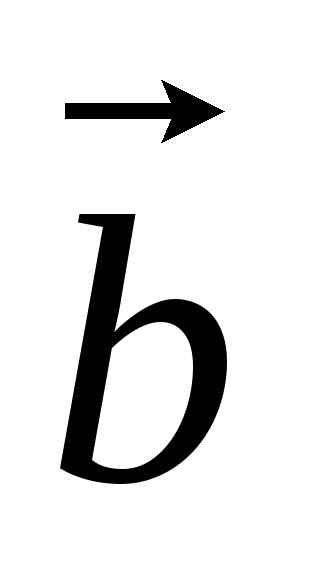
8	Смешанное произведение	Определение ориентации векторов в пространстве: Если ()0, то тройка векторов ,, – правая; если ()0, то тройка векторов ,, 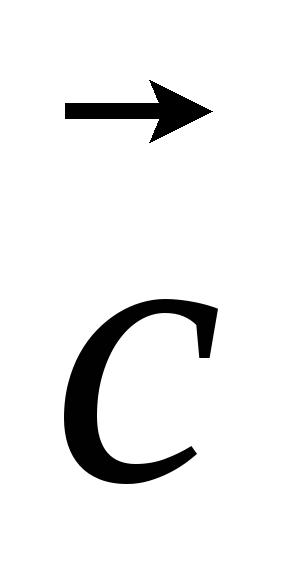– левая.
9	Смешанное произведение	Условие компланарности трех векторов: Если 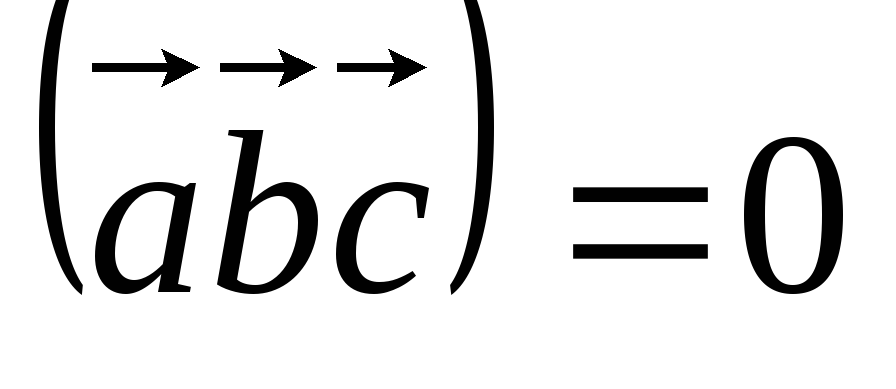, то векторы ,, 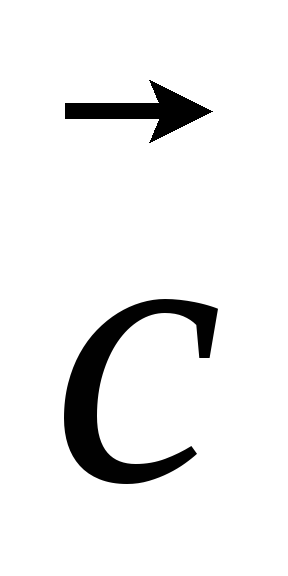компланарны.
10	Смешанное произведение	Установление компланарности четырех точек (принадлежности одной плоскости): Если 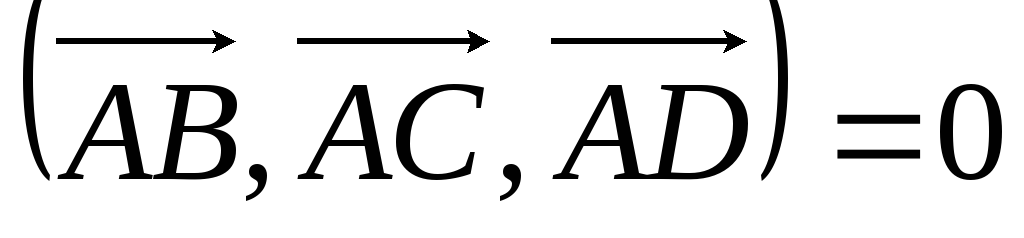, то точки А, B, C, D лежат в одной плоскости.

10