Раздел 2. Элементы векторной алгебры

Лекция 8. Скалярное, векторное и смешанное произведения векторов

Вопросы.

10. Векторная и числовая проекции вектора на ось, вектор.

11. Скалярное произведение: определение, свойства.

12. Скалярное произведение векторов в ортонормированном базисе. Геометрический и механический смысл скалярного произведения. Вычисление длины вектора и угла между двумя векторами.

13. Орт вектора. Направляющие косинусы вектора в V₂ и V₃. Соотношение, связывающее направляющие косинусы вектора в V₂ и V₃.

14. Ориентация пространства. Правая и левая тройки векторов. Правило правого винта.

15. Векторное произведение: определение и свойства (Антикоммутативность, дистрибутивность. Векторное произведение коллинеарных векторов).

16. Векторное произведение векторов в ортонормированном базисе.

17. Геометрический и механический смысл векторного произведения. Вычисление площадей параллелограммов и треугольников.

18. Двойное векторное произведение трех векторов и его свойства.

19. Смешанное произведение трех векторов. Определение, свойства.

10. Проекции вектора

Определение 24.

В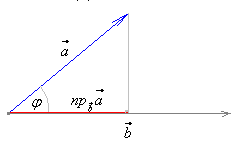екторной проекцией вектора на ось (вектор) называется вектор, начало и конец которого есть соответственно проекции начала и конца данного вектора на данную ось в заданном направлении (в направлении проектирования, заданном плоскостью).

Числовой (скалярной) проекцией вектора на ось или вектор называется скалярная величина .

Это есть абсолютная величина векторной проекции, взятая со знаком плюс или минус в зависимости от угла между векторами. Проекция:

положительна (),

отрицательна (),

нулевая ().

11. Скалярное произведение Основные понятия и определения

Определение 25.

Скалярным произведением двух векторов и называется число, равное произведению модулей этих векторов на косинус угла между ними

(8.1)

Из определения следует:

1)  (2), где – угол между и .

2) условие перпендикулярности двух ненулевых векторов: если векторы перпендикулярны (ортогональны), то =0

Свойства скалярного произведения векторов:

1. . Скалярный квадрат вектора равен квадрату его модуля.

Доказательство по определению (самостоятельно)

2. =. Скалярное произведение коммутативно.

Доказательство по определению (самостоятельно)

3. . Для скалярного произведения справедлив дистрибутивный закон.

Доказательство по определению (самостоятельно)

4. . Для скалярного произведения справедлив сочетательный закон относительно скалярного множителя.

Доказательство по определению (самостоятельно)

5. Если =0, то угол , если >0, то угол , если <0, то угол .

6. =. (8.2)

Доказательство по определениям скалярного произведения и проекции вектора на вектор (самостоятельно)

12. Скалярное произведение векторов, заданных координатами в ортонормированном базисе

Пусть дан базис и векторы и координатами:

, т.е. ,

, т.е.

Вычислим скалярное произведение, предварительно вычислив скалярное произведение ортов:

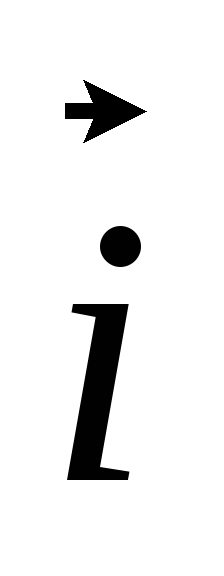
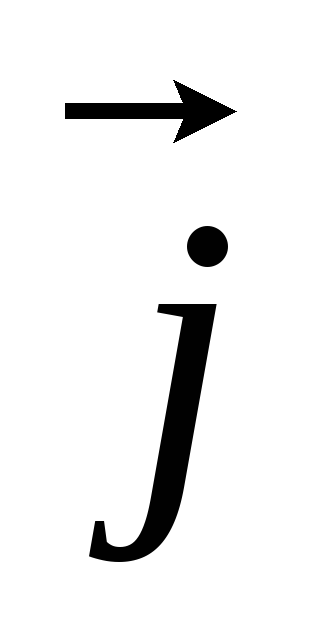
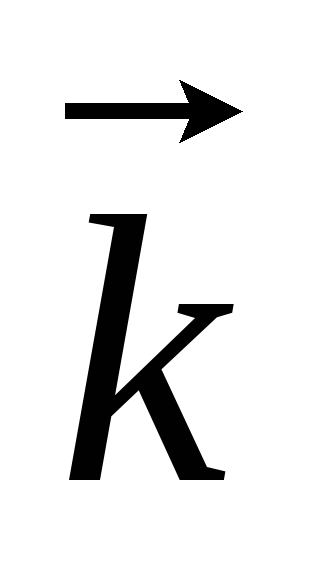
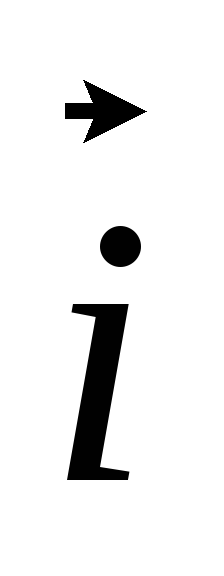
	1	0	0
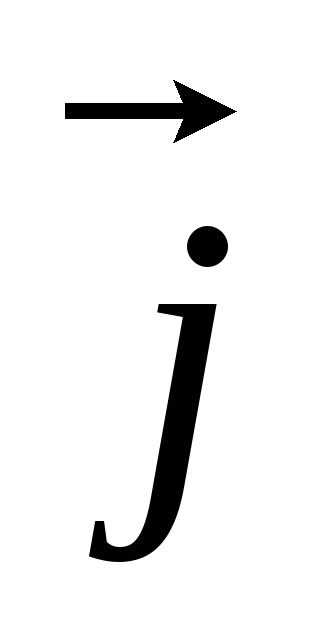
	0	1	0
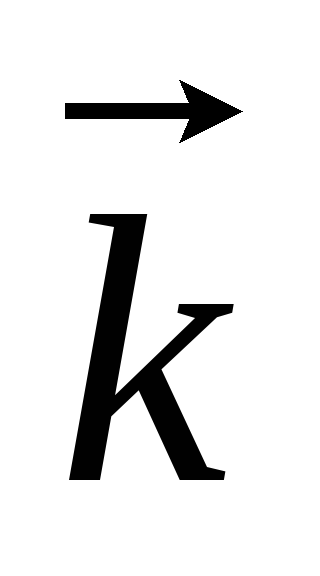
	0	0	1

Тогда =()()=

==

=.

Таким образом, =. (8.3)

Вывод. Скалярное произведение векторов, заданных координатами в декартовой системе координат, равно сумме произведений одноименных координат.

Примечание. Формула справедлива только в ортонормированном базисе .