
- •«Национальный исследовательский ядерный университет «мифи»
- •Элементы векторной алгебры и аналитической геометрии . Пределы и производные функции одной переменной
- •Предисловие
- •Элементы векторной алгебры и аналитической геометрии
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение векторов
- •Элементы аналитической геометрии
- •Уравнения плоскости
- •Уравнения прямой
- •Уравнения прямой в пространстве
- •2. Уравнение прямой на плоскости.
- •Матрицы и их приложения
- •Обратные матрицы
- •Элементы математического анализа Пределы и непрерывность
- •Производная функции
- •Основные правила дифференцирования
- •Дифференцирование сложной функции
- •Производные высших порядков
- •Контрольная работа № 1 Элементы линейной алгебры и аналитической геометрии
- •Контрольная работа № 2 Предел и производная функции одной переменной
Производная функции
Производная функция
![]() от функции
от функции![]() в данной точке
в данной точке
![]() определяется равенством
определяется равенством
 .
.
Таблица производных выглядит следующим образом:
1.
![]() . 2.
. 2.
![]() .
.
3.
 ,
в частности
,
в частности
 .
.
4.
![]() , в частности
, в частности
![]() .
.
5.
![]() .
9.
.
9.
 .
.
6.
![]() .
10.
.
10.
 .
.
7.
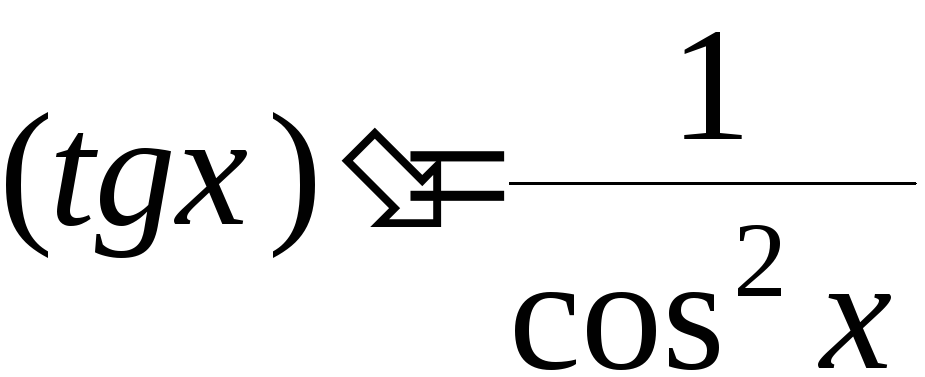 .
11.
.
11.
![]() .
.
8.
 .
12.
.
12.
 .
.
Основные правила дифференцирования
1.
![]() 2.
2.
![]() , в частности,
, в частности,![]() 3.
3.
 , где
, где
![]()
Задача 21. Найти производные следующих функций:
а)
 ;
б)
;
б)
 .
.
Решение. а) Преобразуем выражение в скобках, переходя к дробным и отрицательным показателям. Получим
 .
.
Используя правило
дифференцирования произведения и суммы
находим

 =
=
=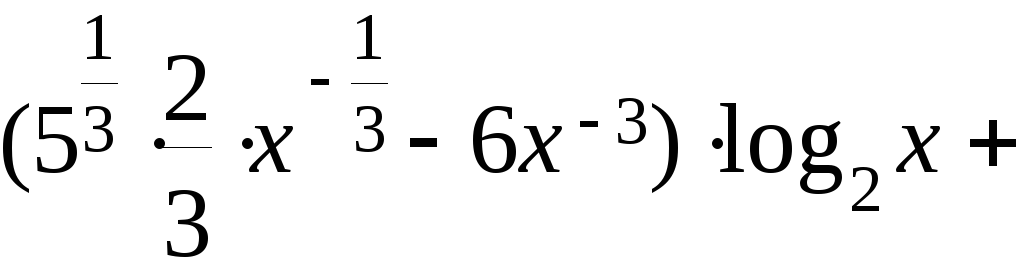
 .
.
б) Проведем предварительное преобразование функции:
 =
= .
.
Используя правила дифференцирования произведения, суммы и частного, получим
 =
=
=

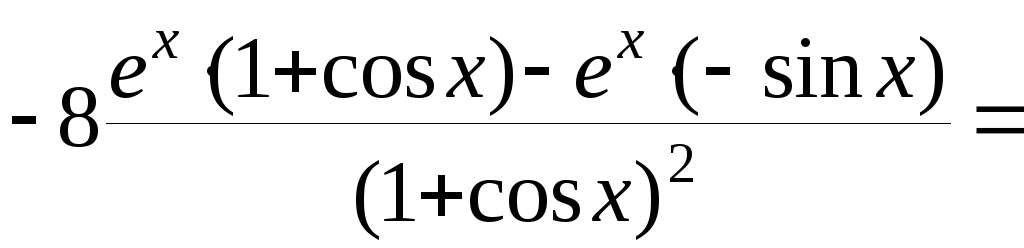
 .
.
Дифференцирование сложной функции
Если функция
![]() дифференцируема в точке
дифференцируема в точке
![]() , а функция
, а функция
![]() дифференцируема в точке
дифференцируема в точке
![]() ,
то сложная функция
,
то сложная функция
![]() дифференцируема в точке
дифференцируема в точке
![]() и
и
![]() ,
,
где индекс внизу показывает, по какой переменной берется производная.
Задача 22. Найти производные следующих функций:
а)
![]() ; г)
; г)
 ;
;
б)
![]() ;
д)
;
д)
![]() .
.
в)
![]() ;
;
Решение.
а) Функцию
![]() представим как композицию функций
представим как композицию функций
![]() и
и
![]() .
Используя таблицу производных, находим:
.
Используя таблицу производных, находим:
![]() ,
,
![]() .
.
Тогда
![]()
![]() .
.
б) Функцию
![]() представим как композицию функций
представим как композицию функций
![]() ,
,
![]() и
и
![]() .Найдем производные по промежуточным
аргументам:
.Найдем производные по промежуточным
аргументам:
![]() ,
,
![]() и
и
 .
.
Производную
сложной функции находим по формуле
![]() .
Окончательно получим
.
Окончательно получим
 =
=![]()
 .
.
Аналогично решается задача в:
![]()
![]()
 =
=
=![]()
![]()
![]()
 =
=![]()
![]()
 .
.
г) Предварительно упростив выражение, определяющее функцию, до вида
 ,
,
находим производную:
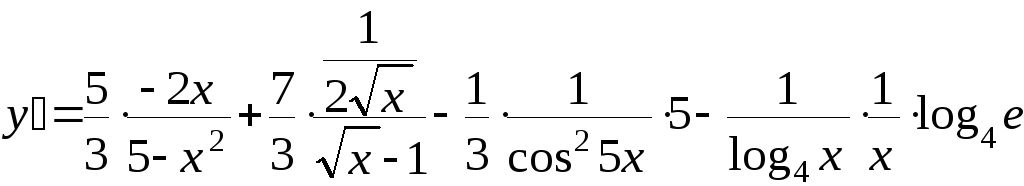 .
.
д) Прологарифмируем обе части равенства, задающего функцию
![]() .
.
Находя производные от левой и правой частей этого тождества, получим

Вычисляя производную
от правой части тождества и решая
уравнение относительно
![]() ,
получим
,
получим
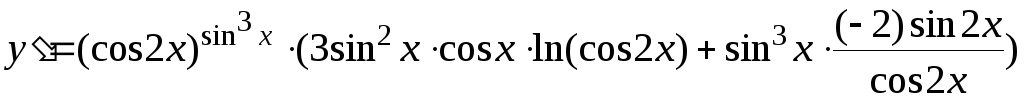 .
.
Производные высших порядков
Производная от
функции
![]() также определяется функцией от
также определяется функцией от
![]() и может быть дифференцируема.
и может быть дифференцируема.
Производная от
производной функции
![]() называется производной второго порядка
от функции
называется производной второго порядка
от функции
![]() и обозначается:
и обозначается:
![]() .
.
Аналогично определяются производные третьего, четвертого и более высоких порядков.
Задача 23. Найти
![]() и
и
![]() для функции
для функции
![]() ;
;
Решение.
Найдем сначала
![]() :
:
![]() =
=![]() =
=![]() .
.
Затем находим вторую производную:
![]() =
=
![]() .
.
Контрольная работа № 1 Элементы линейной алгебры и аналитической геометрии
1.1-1.10.
Даны векторы a![]() ,
b
,
b![]() ,
c
,
c![]() и
d
и
d![]() в некотором
базисе. Показать, что векторы a,b,c
образуют
базис, и найти координаты вектора d
в этом базисе.
в некотором
базисе. Показать, что векторы a,b,c
образуют
базис, и найти координаты вектора d
в этом базисе.
1.1. а(1,2,3),b(-1,3,2),c(7,-3,5),d(6,10,17)
1.2. a(4,7,8), b(9,1,3), c(2,-4,1), d(1,-13,-13)
1.3. a(8,2,3), b(4,6,10), c(3,-2,1), d(7,4,11)
1.4. a(10,3,1), b(1,4,2), c(3,9,2), d(19,30,7)
1.5. a(2,4,1), b(1,3,6), c(5,3,1), d(24,20,6)
1.6. a(1,7,3), b(3,4,2), c(4,8,5), d(7,32,14)
1.7. a(1,-2,3), b(4,7,2), c(6,4,2), d(14,18,6)
1.8. a(1,4,3), b(6,8,5), c(3,1,4), d(21,18,33)
1. 9. a(2,7,3), b(3,1,8), c(2,-7,4), d(16,14,27)
1.10. a(7,2,1), b(4,3,5), c(3,4,-2), d(2,-5,-13)
1.11-1.20.
Даны координаты вершин пирамиды
![]()
![]()
![]()
![]() .
Найти:
.
Найти:
-
длину ребра

 ;
;
-
угол между ребрами

 и
и

 ;
;
3) угол между ребром
![]()
![]() и гранью
и гранью
![]()
![]()
![]() ;
;
4) площадь грани
![]()
![]()
![]() ;
;
5) объем пирамиды;
6) уравнение прямой
![]()
![]() ;
;
7) уравнение
плоскости
![]()
![]()
![]() ;
;
8) уравнение высоты,
опущенной из вершины
![]() на
грань
на
грань
![]()
![]()
![]() .
Сделать чертеж.
.
Сделать чертеж.
1.11.
![]()
1.12.
![]()
1.13.
![]()
1.14.
![]()
1.15.
![]()
1.16
![]()
1.17.
![]()
1.18.
![]()
1.19.
![]()
1.20.
![]()
1.21-1.30. Дана система линейных уравнений

Доказать ее совместность и решить двумя способами: 1) методом Крамера; 2) медотами матричного исчисления.
1.21.
 1.22.
1.22.

1.23.
 1.24.
1.24.

1.25.
 1.26.
1.26.

1.27.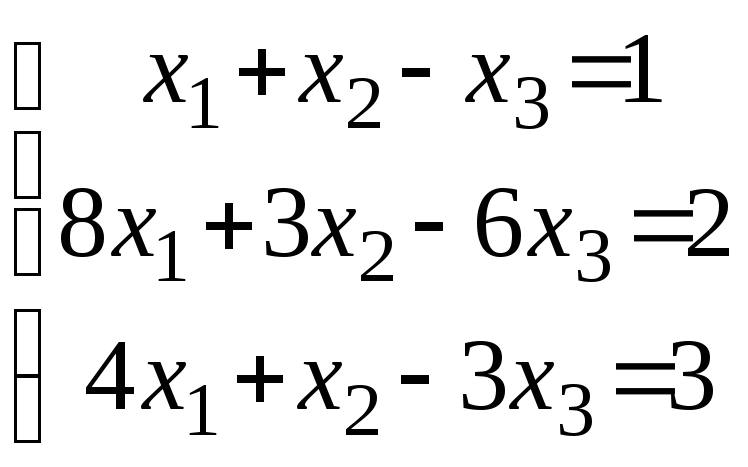 1.28.
1.28.
1.29.
 1. 30.
1. 30.
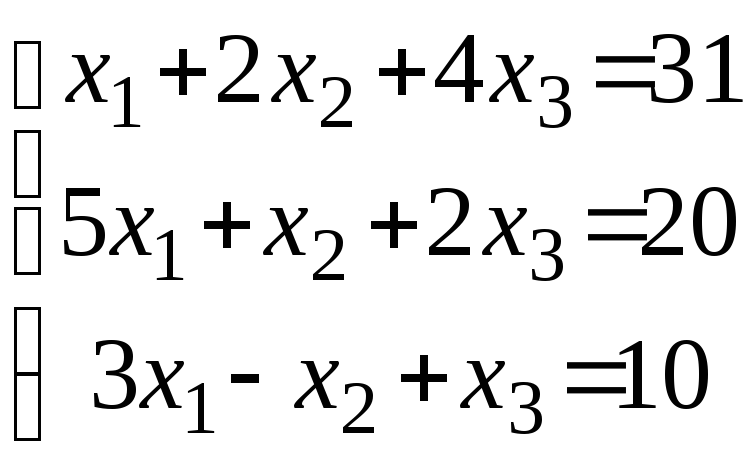
Библиографический список
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1976. - 200 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Т.2.-M.: Наука, 1985.- 560 с.
