Векторное произведение векторов

Пусть - угол между векторами и . Тогда векторным произведением вектора на вектор называется вектор , который:

1) имеет длину, численно равную площади параллелограмма, построенного на векторах и , как на сторонах, т.е. ;

2) перпендикулярен векторам и и направлен так, что если смотреть с конца его, то кратчайший поворот от вектора к вектору будет виден как поворот против хода часовой стрелки.

Если векторы заданы координатами в базисе и , то

.

Задача 7. Вычислить площадь треугольника с вершинами .

Решение. Найдем вначале площадь параллелограмма, построенного на векторах как на сторонах. По определению векторного произведения . Но

.

Тогда .

Следовательно, .

Смешанное произведение векторов

Смешанным произведением трех векторов называется выражение вида .

Если векторы заданы своими координатами в некотором ортонормированном базисе , то

. (3)

Известно, что объем параллелепипеда, построенного на векторах и определяется равенством . Тогда объем пирамиды

.

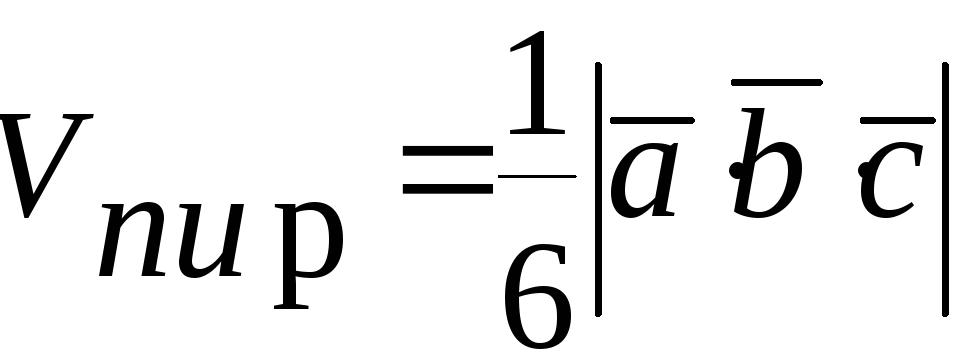Из формулы (3) следует, что векторы будут компланарными тогда и только тогда, когда =0.

Задача 8. Вычислить объем пирамиды с вершинами .

Решение. Найдем координаты векторов . Очевидно, что .

Тогда . Но

. .

Следовательно, .

Задача 9. Даны 4 вектора: . Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение. Докажем вначале, что векторы - линейно независимы. Пусть линейная комбинация векторов обращается в нуль, т. е.

. (4)

Представим векторы в виде линейной комбинации базисных векто-ров , воспользовавшись тем, что координатами вектора являются коэффициенты в разложении вектора по базису:

. (5) Подставляя полученные выражения для и в равенство (4), находим .

Векторы - линейно независимые. Следовательно, коэффициенты в полученной линейной комбинации равны нулю:

(6)

Вычисляя главный определитель этой системы, находим

.

Так как главный определитель линейной однородной системы (6) отличен от нуля, то система имеет только нулевые решения. Следовательно, . Таким образом, из равенства (6) следует, что все коэффициенты , где равны нулю. Последнее означает линейную независимость векторов . Так как этих векторов три, то в трехмерном векторном пространстве они образуют базис. Найдем координаты вектора в базисе . Пусть

. (7)

Так как , a векторы имеют вид (5), то, подставляя эти выражения в (7), получим

.

Векторы образуют базис, поэтому

Решая последнюю систему методом Крамера, получим

; ;

.

Ответ: .