лекции / lekcii_osnovy_teorii_sistem_upravleniya / 1

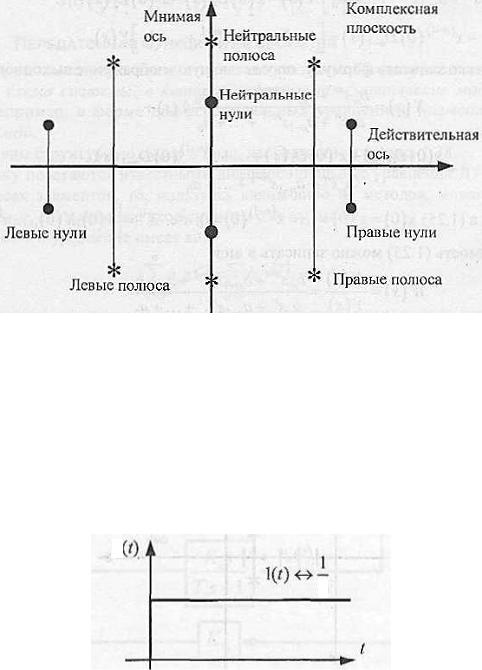
Рис. 1.39. Нули (•) и полюса (*) на комплексной плоскости

Нули и полюса называются левыми (правыми), если они расположены в левой (провой) части p- плоскости, и нейтральными или нулевыми, если они лежат соответственно намнимой оси или в начале координат.

7. ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА СИСТЕМЫ, ПЕРЕХОДНЫЙ

ПРОЦЕСС, ПЕРЕХОДНЫЙ (ДИНАМИЧЕСКИЙ) И УСТАНОВИВШИЙСЯ (СТАТИЧЕСКИЙ) РЕЖИМЫ РАБОТЫ САУ

Введем понятия установившегося (статического) и неустановившегося (динамического) режимов работы системы, рассматривая частный случай, когда x(t) = l(t) (рис. 1.51).

x

p

Рис. 1.51. Входной ступенчатый сигнал

В связи с тем что отклонение управляемой величины существенно зависит от вида воздействий, места их приложении (которые могут быть различными), то обычно при рассмотрении конкретных автоматических систем приходится задаваться типовыми (тестовыми) наиболее характерными для данной системы воздействиями x(t).

Другими словами, поскольку обычно заранее неизвестно, каким в реальных условиях будет входной сигнал, то при анализе качества выбирается некоторое тестовое входное воздействие. Такой подход вполне оправдан, так как имеется связь между реакцией системы на типовой входной сигнал и ее поведением в реальных рабочих условиях. Кроме того, использование типового воздействия позволяет разработчику сравнить несколько вариантов создаваемой системы. К тому же многие системы управления в процессе эксплуатации подвергаются внешним воздействиям, которые по виду очень близки к тестовым сигналам:

Обычно в качестве такого тестового воздействия принимают воздействие вида скачка x(t) = l(t), являющегося во многих случаях наиболее неблагоприятным. Если в этом случае выходной сигнал удовлетворяет определенным условиям, то часто можно считать, что он тем более будет удовлетворять им и при иных характерных воздействиях.

Примерами ступенчатых сигналов могут быть сброс или увеличение нагрузки, отказ двигателя в системе двухмоторный самолет-автопилот курса.

21

Типовое воздействие можно задать в виде δ - функции (дельта-функции). Например, внезапное вхождение самолета в струю воздуха, движущегося перпендикулярно траектории движения самолета.

При исследовании следящих систем типовыми управляющим воздействием может являться полином. x(t) = x0+ x1t + x 2t2+ ... + xltl, t > 0. (1.62)

В отдельных случаях типовое воздействие может быть сложной формы, например, при исследовании следящих систем управления антенной РЛС используется функция

x(t)= arctg(βt),

которая отражает изменение азимутального угла между направлением на цель и некоторым фиксированным направлением в случае прямолинейного и равномерного движения сопровождаемого объекта (рис. 1.52). Часто типовые воздействия определяются экспериментальным путем.

x x

x

x x

Рис. 1.52. Виды тестовых воздействий

Любое воздействие, поданное на систему, вызывает в ней динамический режим, по окончании которого система переходит в новое установившееся состояние. При статическом отклонении, не равном нулю, можно выделить следующие типы переходных процессов (они определяются составляющей yП(t)

(рис. 1.55):

•колебательные (кривая 1), в которых имеет место два и более перерегулирований;

•малоколебательные (кривая 2), в которых число перерегулирований равно единице;

•без nеререгулирования (кривая З), в которых y(t) ≤y(∞) для всех t [0,∞);

•монотонные (кривая 4), характеризующиеся тем, что скорость изменения выхода не меняет знака в течение всего времени Тр.

22

x

y y

y

y

Рис. 1.55. Основные типы переходных процессов

Реакция системы на единичное ступенчатое воздействие x(t) = 1(t) при нулевых начальных условиях называется переходной характеристикой (ПX) системы (для нее существует специальное обозначение h(t)).

Приведем основные параметры ПХ (рис. 1.56):

•время управления Тp(время переходного процесса) - минимальное время по истечении которого выходная величина будет оставаться близкой к установившемуся значению с заданной точностью:

•перерегyлuрованuе σ, %, определяется выражением

в реальных системах обычно

но в некоторых случаях допускается до 70%;

•статическое отклонение

e

•частота колебаний процесса h(t)

•время установления Tу - абсцисса точки пересечения с уровнем установившегося значения hуст (иногда Tуназывают временем нарастания Tн);

•декремент затухания

23

Tр

Рис. 1.56. Переходная характеристика системы

При синтезе систем обычно задаются допустимыми значениями параметров переходной характеристики, например

Ранее уже отмечалось, что если известны изображения входа X(p) и передаточная функция W(p), то по формуле (1.25) можно найти изображение выхода, а путем обратного преобразования - и сам выходной процесс.

Таким образом, передаточная функция полностью характеризует динамические свойства системы (при нулевых начальных условиях).

Введем понятие дельта-функции δ(t).

Дельта-функцией называется функция, которая обладает следующими свойствами:

Иногда δ(t) вводят как производную от единичной функции l(t), т.е.

Дельта-функция имеет производные любого порядка. Поскольку L{1(t)} = 1/p, то, учитывая (1.113), имеем L{δ(t)}= 1, т.е. изображением δ(t) является единица, Теперь найдем изображение выхода, если входом является δ(t) -дельта-функция. Реакцию САУ на единичное импульсное воздействие, т.е. на δ(t) на входе при нулевых начальных условиях называют импульсной переходной или весовой функцией (ИПФ) системы k(t).

Найдем изображение ИПФ:

Отсюда следует важный факт: передаточная функция равна изображению по Лапласу от ИПФ и соответственно

24

р

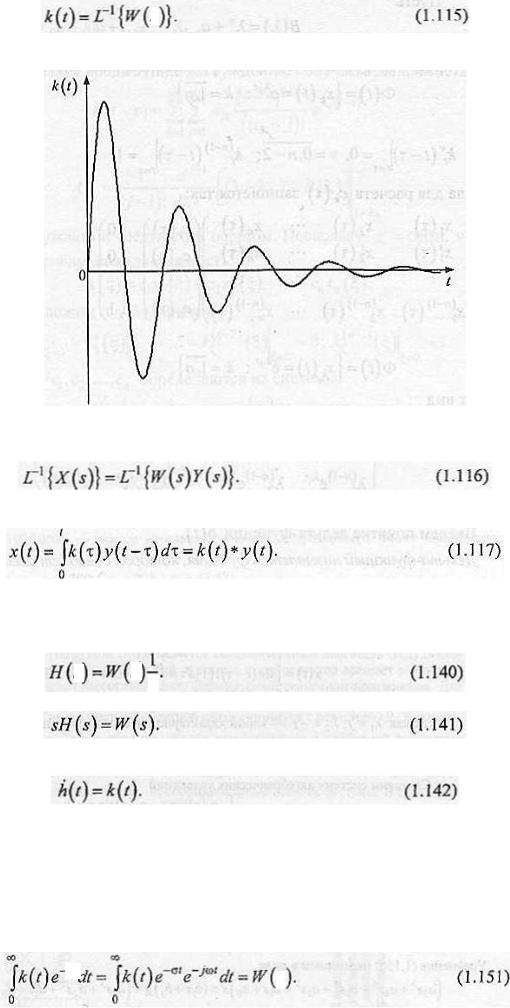
ИПФ, как и передаточная функция, является исчерпывающей характеристикой САУ при нулевых начальных условиях. ИПФ имеет вид, представленный на рис. 1.66.

Рис. 1.66. ИПФ системы

Найдем соотношение, связывающее входной сигнал x(t), выходной процесс y(t) и ИПФ. Имеем

Зависимость (1.116) представляет собой изображение вынужденного сигнала системы; формула для вынужденного процесса во временной области имеет вид

Эта формула, как и зависимость (1.116), справедлива при нулевых начальных условиях. ИПФ может быть построена как обратное преобразование Лапласа от ПФ W(p).

Интегральное соотношение (1.117) называют интегралом свертки или интегралом Дюамеля.

Найдем связь между ИПФ и ПХ. Имеем

p p

p

Отсюда находим

Так как при нулевых начальных условиях умножению изображения на p соответствует дифференцирование в области времени, то из (1.141) следует

9. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ

При рассмотрении вынужденных колебаний систем при подаче на вход гармонических колебаний важную роль играют частотные характеристики. Их роль особенно заметна при исследовании устойчивости, а также при синтезе корректирующих устройств (регуляторов). Особую роль при разработке частотных методов сыграл В.В. Солодовников.

Передаточная функция W(p) определяется зависимостью

pt

p

25

Пусть k(t) абсолютно интегрируема, тогда можно записать (можно положить σ = 0)

Y

X

где

-одностороннее преобразование Фурье выхода;

-одностороннее преобразование Фурье входа. Выражение (1.152) запишем так:

Если

то

Дадим некоторые определения.

Комплекснозначная функция W(jω) называется комплексной частотной характеристикой системы (КЧХ) или амплитудно-фазовой частотной характеристикой (АФЧХ или АФХ).

Функции Р(ω) и Q(ω) называются соответственно действительной и мнимой частотными характеристиками.

Функции А(ω) и (ω) определяемые зависимостями (1.157) и(1.158), называются соответственно амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристиками.

На рис. 1.72 представлены типовые АЧХ и ФЧХ системы.

26

Рис. 1.72. ЛЧХ и ФЧХ системы

Частотные характеристики определяются следующими показателями:

показатель колебательности М = Amax(ω)/А(0) -характеризует склонность системы к колебаниям: чем выше М, тем менее качественна система (как правило, .в реальных системах 1,1 ≤М

1,5 );

резонансная частота ωр - частота, при которой АЧХ имеет максимум (на этой частоте гармонические колебания имеют наибольшее усиление);

полоса пропускания системы - интервал от ω = 0 до ω0, при котором выполняется

условие

Частота среза косвенно характеризует длительность переходного процесса; справедпиво соотношение

р

Таким образом, можно сделать важный вывод: чем шире полоса пропускания, тем система является более быстродействующей.

Если же полоса пропускания является постоянной для всех частот на (-,+∞) (рис. 1.73) и, следовательно, ωср = ∞, то система является безынерционной, у которой Тр= 0. Этот вывод следует из формулы (1.161). Поскольку система с бесконечной полосой пропускания (рис. 1.73) безынерционна, то ИПФ такой системы равна δ(t), а ПХ равна l(t)(т.е. входные сигналы отрабатываются без искажения).

27

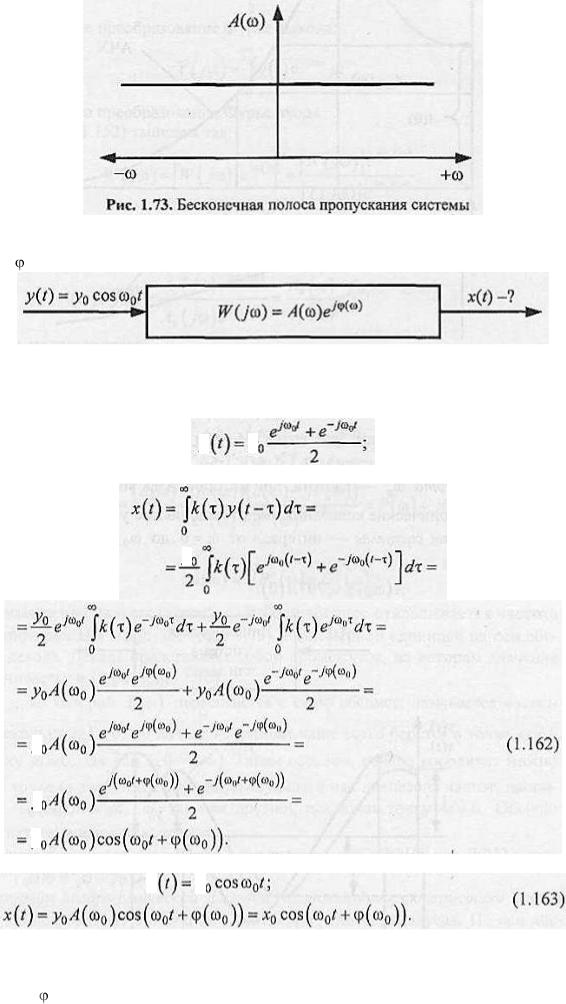
Далее рассмотрим закон преобразования гармонических сигналов линейными системами, имеющими

А(ω) — АЧХ и (ω) – ФЧХ (рис. 1.74).

Рис. 1.74. Преобразование гармонических сигналов

Имеем (рассматривается установившийся режим работы системы, длячего верхний предел интегрирования берется равным ∞)

x x

тогда

x

x

x

x

Результат имеет вид

x x

Результат (1.163) можно трактовать так: если на вход системы подается косинусоидальный сигнал с амплитудой x0, то на выходе в установившемся режиме имеет места также косинусоидальный сигнал с той же частотой, ноуже с другими амплитудой и фазой: амплитуда выхода равна y0= x0А(ωср), а сигнал имеет сдвиг фазы (ω0)

28

В результате в системе возникнет переходный процесс (имеет место составляющая yП(t))и установившиеся колебания с частотой ω0. После затухания переходного процесса (т.е. в установившемся режиме), если система устойчива yП(t)→0 (t → ∞), на в ходе будут иметь место установившиеся колебания с частотой ω0, равной частоте воздействия, но отличающиеся по амплитуде и фазе. Одна точка АЧХ ( А(ω0) и

(ω0) - сдвиг фазы выходного сигнала по отношению ко входу. Аналогично можно построить все точки АЧХ и ФЧХ (рис. 1.75).

y x

Рис. 1.75. Экспериментальное определение частотных характеристик динамической системы (динамического звена):

а - система или звено; б -процессы на входе и выходе

Логарифмические частотные характеристики системы

Логарифмической амплитудно-частотной характеристикой (ЛАЧХ или ЛАХ) системы называется график функции L(ω) вида

где

Единицей измерения является децибел. По оси абсцисс откладывается частота ω[c-1] влогарифмическом масштабе (рис. 1.76). Равномерной единицей на оси абсцисс является декада. Декада представляетсобой промежуток, на котором значение частоты увеличивается в 10 раз (рис. 1.76).

29

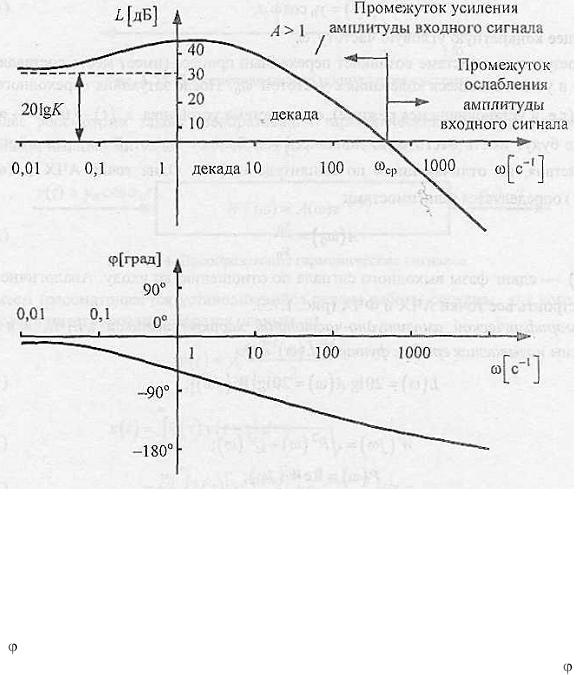
Рис. 1.76. Логарифмические частотные характеристики

Частота ωср, на которой L(ω)пересекается с осью абсцисс, называется частотой среза. Поскольку lg1 = 0, то начало координат чаше всего берется в точке ω = 1 (исключая точку ω = 0, так как lg0 = - ∞). Таким образом, начало координат можно брать в любой точке (в зависимости от интересующего нас диапазона частот, например: ω = 0,05, ω = 0,1, ω = 1, ω = 10 или другие), исключая точку ω = 0. Обычно начало координат помещают в точке ω = 1.

Логарифмической фазовой частотной характеристикой (ЛФЧХ или ЛФХ) называется график зависимости (ω)= ArgW(jω).

При построении логарифмической фазовой частотной характеристики отсчет углов идет по оси ординат в обычном масштабе в угловых градусах. По оси абсцисс откладывается по-прежнему частота ω в логарифмическом масштабе.

Важно иметь в виду, что ось абсцисс соответствует значению А = 1, т.е. прохождению амплитуды входного сигнала через звено в натуральную величину. Верхняя полуплоскость ЛАЧХ соответствует значениям А >1 (усиление амплитуды), а нижняя полуплоскость - значениям А <1 (ослабление амплитуды).

30