лекции / lekcii_osnovy_teorii_sistem_upravleniya / 1

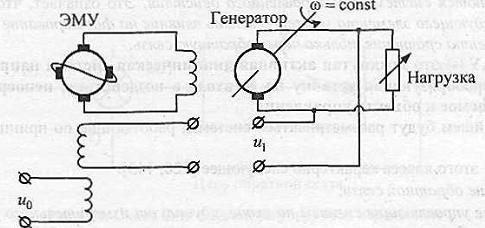
достаточно мощные воздействия на объект (ток в цепи нагрева);

•ошибка e(t) является движущим сигналом для системы, работающей на уменьшение этой ошибки;

•САУ является замкнутой системой, замыкание осуществляется через обратную связь (ОС), которая, в свою очередь, реализуется с помощью измерительного устройства (термопары); измерительный (чувствительный) элемент служит не просто для регистрации температуры, а для формирования рассогласования e(t), являющегося входом усилителя и, таким образом, реализующего процесс управления.

Взависимости от характера изменения входного (задающего) управляющего воздействия x(t) САУ могут быть подразделены на три основных типа

1.системы автоматической стабилизации (или системы автоматического регулирования). В нихуправляющие воздействия представляют собой заданные постоянные величины (уставки);

2.системы программного управления. В них управляющие воздействия являются известными функциями времени (изменяются по программе);

3.следящие системы.В них задающие воздействия представляют собой заранее неизвестные функции времени.

Если в САУ, показанной на рис. 1.8, входной сигнал сохраняет постоянное значение (движок потенциометра неподвижен), то она представляет систему автоматической стабилизации угловой скорости электродвигателя. Постоянное значение, которое имеет входной сигнал, называется настройкой (ycmaвкой автоматического регулятора.Уставке соответствует требуемое значение регулируемой величины объекта. Система автоматического управления температурой в электропечи для закалки металла является

системой программного управления, если процесс изменения температуры является известной функцией времени x(t).

Типовой следящей системой является система автоматического сопровождения цели по соответствующим координатам (рис. 1.9).

Приведем некоторые положения, характеризующие такое важное понятие, как качество управления (все положения далее будут теоретически обоснованы).

Дадим следующее определение:

Объекты, обладающие свойством возвращаться к своему прежнему состоянию после устранения причин, вызвавших изменение этого состояния, можно назвать устойчивыми.

Неустойчивая система, как правило, не может выполнить возлагаемых на нее задач и поэтому оказывается непригодной для эксплуатации.

Обсудим физическое содержание явления неустойчивости.

Рис. 1.13

Система управления (рис. 1.13) состоит из генератора напряжения и электромашинного усилителя. Разомкнем систему на выходе электромашинного усилителя и подадим на вход такой разомкнутой системы напряжение, изменяющееся скачком на величину и0. В такой разомкнутой системе возникает некий переходный процесс (рис. 1.14). С течением времени напряжение на нагрузке генератора станет равным некоторому установившемуся значению

u1= k·u0,

где k = kрkэму - коэффициент усиления разомкнутой системы, равный произведению коэффициентов

11

усиления ее элементов. k представляет собой отношение напряжения u1 на выходе системы к напряжению и0на входе системы в установившемся режиме, В замкнутой системе (рис. 1.14) на усилитель воздействует не и0 , как это было в разомкнутой системе, а разность напряжений

u = и0- u1,

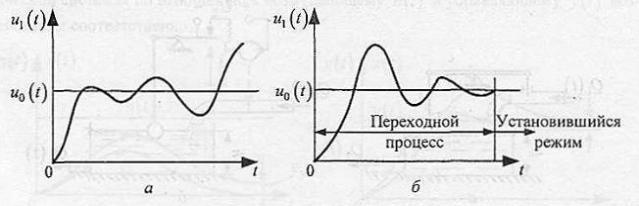
представляющая собой отклонение регулируемой величины от заданной, или ошибку. При изменении и0скачком в замкнутой системе (рис. 1.14) напряжение u1,а значит, и напряжение на нагрузке в начальный промежуток времени после момента приложения напряжения и0в силу инерционности системы будут изменяться так же, как и в разомкнутой системе. Однако в последующие моменты времени характер изменения напряжения u1в замкнутой системе будет иным, так как в замкнутой системе на усилитель воздействует теперь не постоянное напряжение и0, а величина u = и0- u1, зависящаяся от самого напряжения u1При достаточно большом коэффициенте усиления k малые изменения uвызовут значительные изменения тока возбуждения генератора, а значит, и напряжения на нагрузке, что приведет к увеличению отклонения и. Это, в свою очередь, может еще более увеличить ток возбуждения генератора и т.д., Изменение напряжения и, во времени будет иметь характер, приведенный на рис. 1.14, ат.е. напряжение на нагрузке не будет стремиться ни к какому установившемуся значению, что характеризует неустойчивость системы. Если же коэффициент усиления не столь велик, то отклонения напряжения и могут с течением времени уменьшаться и стремиться к установившемуся значению. При этом напряжение генератора u1, а значит, и напряжение на нагрузке будет стремиться к постоянной величине (рис. 1.14, б), что соответствует устойчивости системы. Эти общие рассуждения имеют своей целью физически пояснить причины неустойчивости системы.

Рис 1.14. Процессы изменения u1(t)

Из приведенных рассуждений следует, что для обеспечения устойчивой работы системы нужно уменьшить коэффициент усиления, k. Но, с другой стороны, для уменьшения отклонения управляемой величины от заданного значения в установившемся режиме, необходимо увеличить значение коэффициента усиления k. Это обстоятельство иллюстрирует характерное для систем «противоречие» между точностью и устойчивостью автоматической системы. Стремление к высокой точности требует увеличения k, а увеличение k приводит к неустойчивости. Изменяя параметры системы, можно добиться того.что система станет устойчивой и при заданном коэффициенте усиления системы k. Следует отметить, однако, что практически мы часто ограничены ввозможности изменения параметров систем в широких пределах.

Иногда может оказаться, что устойчивость системы недостижима ни при каком изменении параметров системы. В этом случаеустойчивости можно добиться лишь при изменении структуры системы. Автоматические системы, в которых устойчивая работа системы не может быть достигнута никаким изменением параметров системы, называют структурно неустойчивыми системами.

И, наконец.обсудим еще одно важное свойство САУ, связанное с качеством управления.

4.СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САУ

САУ подразделяются на сmаmuческие u асmаmuческие в завucuмостu от того, имеют или не имеют они ошибку в установившемся состоянии при определенных воздействиях (понятие установившегося состояния иллюстрируется рис. 1.14).

На рис. 1.15 приведена схема статической САУ уровня воды в резервуаре с помощью поплавкового регулятора. Поплавок в ней жестко связан с регулирующим элементом органом - задвижкой, которая изменяет количество воды, поступающей в единицу времени по питающей трубе врезервуар. Данная

12

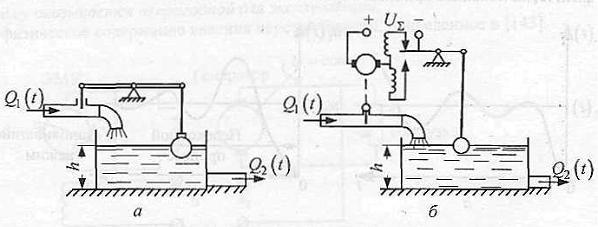
система - пример статического управления, при котором управляемая величина при разных, но постоянных внешних воздействиях на объект по окончании переходного процесса принимает различные значения, зависящие от значения внешнего воздействия (нагрузки). Чем больше расход жидкости Q(t) в системе, чем больше открыта задвижка, и, следовательно, тем ниже в состоянии равновесия будет находиться поплавок.

Характерные особенности статической системы управления следующие:

•равновесие системы имеет место при различных значениях управляемой величины;

•каждому значению управляемой величины соответствует единственное определенное положение регулирующего элемента;

•контур регулирования системы должен состоять из статических звеньев, осуществляющих зависимость y = f(x).

Рис 1.15. Статическая САУ уровня жидкости (а) и астатическая (б)

Всхему САУ уровня жидкости (рис. 1.15) включен электродвигатель постоянного тока. При увеличении (уменьшении) расхода жидкости поплавок (чувствительный элемент) опускается (поднимается)

изамыкает верхний (нижний) контакт. При этом электродвигатель начинает вращаться в таком направлении, чтобы поднять (опустить) задвижку - регулирующий элемент - и увеличить (уменьшить) приток жидкости. Данная схема - пример астатического управления, когда приразличных постоянных значениях внешнего воздействия на объект отклонение управляемой величины от требуемого значения по окончании переходного процесса становится равным нулю. Степень открытия заслонки зависит от расхода жидкости, а поплавок при заданном значении уровня занимает одно определенное положение, соответствующее заданному. Связать поплавок и заслонку следует таким образом, чтобы одному положению поплавка могло соответствовать любое положение заслонки.

Характерные особенности астатической системы управления следующие:

• равновесие системы имеет место при единственном значении управляемой величины, равном заданному;

• регулирующий элемент должен иметь возможность занимать различные положения при одном итом же значении управляемой величины.

Вастатических системах первая особенность реализуется с некоторой погрешностью, так как чувствительный элемент обладает разрешающей способностью (нечувствительностью). Для осуществления указанной связи между чувствительным к регулирующим элементами в контур регулирования должно быть введено астатическое звено - в данном случае электродвигатель. При отсутствии напряжения вал электродвигателя неподвижен в любом положении, при наличии напряжения он непрерывно вращается. Астатическое звено находится в состоянии так называемого безразличного равновесия при отсутствии внешнего воздействия и выходит из равновесия при наличии этого воздействия.

Следует также различать системы статические и астатические по отношению к возмущающему n(t) и управляющему x(t) воздействию.

Всистемах, статических поотношению к возмущающим воздействиям, не одинаковым по постоянной величине, этим воздействиям соответствуют различные значения управляемой величины. В астатических системах значение управляемой величины остается постоянным, равным заданному, и не зависит от значения возмущающего воздействия.

Всистемах, статических по отношению к управляющим воздействиям, постоянным значениям этого воздействия соответствует постоянная ошибка, значение которой зависит от значения управляющего

13

сигнала. В астатических системах после окончания переходного процесса ошибка равна нулю.

На рис. 1.16, а-б приведены кривые переходныхпроцессов в статической и астатической системах по отношению к возмущающему n(t) и управляющему x(t) воздействиям соответственно.

y(t)

e

Рис. 1.16. Переходные процессы в статической (кривая 1) и астатической (кривая 2) системах по отношению к возмущающему (а) и управляющему (б) воздействиям

Рассмотрим более сложную систему управления уровнем жидкости. Большинство таких САУ построены по схеме, показанной на рис. 1.17.

e

Рис. 1.17. Принципиальная схема системы автоматического регулировании уровня жидкости: П - привод; РК - регулируемый клапан; РМ - расходомер; УМ - уровнемер;

БИК -блок извлечения корня

Уровень жидкости h(t) зависит от разности двух величин - притока GП и расхода GР. Если GП>GР, то уровень растет, и наоборот, при GП<GР - h(t) уменьшается.

Величину притока GП можно менять посредством регулирующего клапана РК, который управляется.электроприводом П.

Сигнал, соответствующий действительному уровню h(t), измеряется уровнемером (УМ) и сравнивается с требуемым уровнемh3(уставкой).

В зависимости от величины и знака рассогласования e(t) регулятор посредством электропривода увеличивает, если e>0, или уменьшает, если e<0, приток жидкости GП, поддерживая равенство между GПи GР при заданном уровне h3.

Изменение расхода GР нарушает баланс в схеме. Поэтому GР, является возмущающим сигналом. Для повышения точности регулирования наряду с e (t) используется сигналы GП и GP, которые

порождают местную обратную связь. При использовании GP имеет место так называемое комбинированное регулирование по отклонению и возмущению.

Выходной сигнал некоторых расходомеров пропорционален квадрату расхода жидкости. Поэтому цепи измерения расходов содержат блоки извлечения корня (БИК)

14

Воспользуемся стандартными обозначениями: x(t) = h3 - вход системы (заданное воздействие), y(t) = h(t) - выход системы (уровень жидкости), n(t) = GП(t) -возмущение (расход жидкости),

Функциональная схема САУ уровнем жидкости может быть представлена в виде, изображенном на рис. 1.18.

Рис, 1.18.- Функциональная схема СЛУ уровнем жидкости:

1 - задающее устройство; 2 - сравнивающее устройство; 3 - регулятор; 4 - усилитель мощности; 5 - привод; 6 - регулирующий орган (клапан); 7 -объект управления; 8 - уровнемер; 9,10 - линейные расходомеры

5.ТИПОВАЯ ФУНКЦИОНАЛЬНАЯ СХЕМА СИСТЕМЫ

Создание систем автоматического управления, особенно таких, которые проектируются впервые и которые включают элементы, в основу работу которых положены разные физические законы (ракета; РЛС; электрические и пневматические устройства и др.) - процесс сложный, требующий обширных знаний в различный областях науки и большого опыта работы (творческих навыков).

Прежде чем переходить к задачам проектирования, рассмотрим типовую функциональную схему системы автоматического управления. Рассмотренные выше примеры САУ позволяют представить типовую функциональную схему (рис. 1.32). Функциональное назначение каждого из элементов типовой схемы состоит в следующем.

y

Рис. 1.32. Типовая функциональная схема САУ:

1 - задающее устройство: 2, 5 - сравнивающие устройства; 3 - преобразующее устройство;

• 4,8-корректирующие устройства (регулятор); 6 -усилительное устройство; 7 - исполнительное устройство; 9 — чувствительные или измерительные элементы; 10 - элемент главной

обратной связи; 11 - объект управления; n(t) -помеха

Задающее устройство преобразует воздействие в сигнал x(t), а сравнивающее устройство путем сравнения сигнала x(t) и управляемой величины y(t) (предполагается, что 9 и 10 не искажают сигнал y(t) вырабатывает сигнал ошибки e(t). Иногда сравнивающее устройство называют датчиком ошибки, отклонения или рассогласования.

Преобразующее устройство 3 служит для преобразования одной физической величины в другую, более удобную для использования в процессе управления (во многих системах преобразующее устройство отсутствует).

15

Регулятор 4, 8 служит для обеспечения заданных динамических свойств замкнутой системы.

Например, с его помощью обеспечивается высокая точность работы в установившемся режиме, демпфируютcя колебания для сильно колебательных объектов (например летательных аппаратов). Более того, введение в систему регулятора позволяет устранить незатухающие или возрастающие колебания управляемой величины. Иногда регуляторы вырабатывают управляющие сигналы (команды) в зависимости от возмущающих воздействий, что существенно повышает качество работы систем, увеличивая их точность. Из схемы САУ видно, что в хорошо спроектированной системе ошибка e(t) должна быть мала. Вместе с тем на объект должны поступать достаточно мощные воздействия. Мощности же сигнала e(t) совершенно недостаточно для питания даже небольшого двигателя. В связи с этим важным элементом САУ является усилительное устройство, предназначенное для усиления мощности сигнала ошибки e(t). Усилитель управляет энергией, поступающей от постороннего источника. На практике широко используются электронные, магнитные, гидравлические, пневматические усилители.

Следующим важным элементом САУ является исполнительное устройство, предназначенное для воздействия на управляющий орган. В системах управления используются следующие типы исполнительных устройств: пневматические, гидравлические и электрические, подразделяемые, в свою очередь, на электромоторныеи электромагнитные.

Пневматические исполнительные устройства имеютсравнительномалые габариты и массу, но требуют большого расхода сжатого газа.

Гидравлические исполнительные устройства способны преодолевать большие нагрузки и практически безынерционны. Недостаток - большая масса. Электрические исполнительные устройства достаточно универсальны в применении и отличаются простотой канализации подводимой к ним энергии. Вместе с тем их использование требует наличия достаточно мощного источника тока. В некоторых САУ исполнительный механизм как таковой отсутствует и воздействие на объект осуществляется изменением состояния какой-либо величины (тока, напряжения) без помощи механических устройств.

Чувствительные или измерительные элементы (датчики) необходимы для преобразования управляемых переменных всигналы управления (например, преобразованиявида «угол-напряжение»).

Элемент, который подвергается управлению, называют объектом управления. При проектировании систем объектом управления считают всю неизменяемую часть системы (все элементы, кроме регулятора). Им может быть электрическая печь для закаливания металла, самолет, ракета, космический аппарат, двигатель, ядерный реактор, станок для обработки металла и т.д. В связи с большим разнообразием объектов управления разными могут быть и управляемые переменные: напряжение, число оборотов, угловое положение, курс, мощность и т.д. Изучением конструкций объектов занимаются специальные дисциплины: электротехника, авиация и космонавтика, самолетостроение, энергетика, ядерная техника, турбостроение, двигателестроение и т.д.

Из рассмотрения рис. 1.32 можно сделать вывод, что САУ представляет собой замкнутую систему,

обладающую свойством однонаправленности и реагирующую на сигнал ошибки e(t). Можно заключить, что система включает функционально необходимые элементы (неизменяемая часть системы), т.е. элементы, без которых принципиально невозможно работа САУ (объект управления, исполнительный эле мент, усилитель, измерительное устройство), и изменяемую часть, которая вводится для придания системе желаемых свойств, обеспечивающих качество управления, определяемое техническим заданием (регулятор системы).

На первом этапе расчета и проектирования систем автоматического управления (САУ) ограничиваются качественным описанием систем и в связи с этим рассматривают их функциональные схемы. Такое описание называют содержательнымили неформальным. Неформальным описанием САУ называется вся имеющаяся совокупность сведений о ней, достаточная для построения фактического алгоритма ее работы. Неформальное описание системы содержит информацию, достаточную для построения ее функциональной схемы. Последняя же служит основой для разработки формального (математического) описания системы.

Недостаток содержательного или неформального описания систем в том, что такой подход не оперирует количественными характеристиками и, таким образом, наука, в основе которой лежит неформальное описание, не является точной наукой, Для решения же задач исследования и проектирования систем необходимо оперировать количественными характеристиками, определяющими качество ее работы,

В связи с этим центральным понятием теории систем является математическая модель или оператор системы.

16

6.МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ.

Под математической моделью САУ понимают количественную формализацию абстрактных представлении об изучаемой системе. Математическая модель - это формальное описание системы с помощью математических средств: дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств, множеств и т.д.

Пользуясь понятием системного оператора, можно на единой основе рассмотреть понятие математической модели САУ.

Пусть X и Y - множества входных и выходных сигналов САУ. Если каждому элементу x X ставится в соответствие определенный элемент y Y, то говорят, что задан системный оператор А.

Связь между входом и выходом системы задается посредством системного оператораА:

Аy = x и y = А-1x

Операторное уравнение (или уравнение с оператором А) Аy = x следует считать математической моделью САУ, поскольку онаустанавливает количественную связь между входом x(t) и выходом y(t) системы.

Принципиально важным является ответ на вопрос: как построить оператор системы и, таким образом, определить ее математическую модель. Ответ на поставленный вопрос состоит в следующем:

математические модели могут быть представлены разными математическими средствами, но важнейшую роль играют дифференциальные и интегральные уравнения, которые получаются на основании фундаментальных физических законов, лежащих в основе функционирования механических, электрических, гидравлических, термодинамических систем.

Дляполучения дифференциального уравнения системы вцепом обычно составляют описание ее отдельных элементов, т.е. составляют дифференциальные уравнения для каждого входящего в систему элемента (например, для САУ (рис. 1.32) составляются дифференциальные уравнения усилителя, привода, реостата, электрической печи, термопары и элемента сравнения).

Совокупность всех уравнений элементов u дает уравнение системы в целом. Уравнения системы определяют ее математическую модель, которая для одной и той же системы в зависимости от цели исследования может быть разной.

Полезно при решении одной и той же задачи на разных этапах строить разные математические модели: начинать проектирование можно с простой модели, а затем ее постепенно усложнять, с тем чтобы учесть дополнительные физические явления и связи, которые на начальном этапе не были учтены как несуществующие.

Вэтой главе будем изучать системы, операторами которых являются линейные дифференциальные и интегральные операторы.

Взависимости от того, какими классами дифференциальных уравнений описываются САУ, их можно укрупнено классифицировать так, как показано на рис. 1.33.

Линейными называют класс систем, описываемый линейными операторными уравнениями

(например, линейными дифференциальными уравнениями или их системами), в противном случае система входит в класс нелинейных систем.

Линейными или нелинейными дискретными системами называются такие системы, которые описываются соответственно линейными или нелинейными разностными уравнениями или системами разностных уравнений.

Линейными или нелинейными стационарными системами называются системы, которые описываются дифференциальными уравнениями или системами уравнений с постоянными коэффициентами.

Нестационарными системами (линейнымиили нелинейными) называют системы автоматического управления, поведение которых описывается дифференциальными уравнениями или системами уравнений с переменными коэффициентами.

Сосредоточенными, или системами с сосредоточенными параметрами.называются системы, поведение которых описывается обыкновенными дифференциальными уравнениями.

Распределенные системы - это системы, которые описываются дифференциальными уравнениями в частных производных.

Уже по приведенной классификации можно судить о степени сложности задачи проектирования САУ. Теоретической базой проектирования САУ в различных отраслях техники, экономики и изучения

систем в живой природе и обществе является теория автоматического управления (ТАУ).

17

Рис. 1.33. Классификация САУ:

1 - система автоматического управления (САУ); 2 - линейные САУ; 3 - нелинейные САУ; 4 - непрерывные СА У; 5 - дискретные САУ;

6 - непрерывнодискретные САУ; 7 - стационарные системы; 8 - нестационарные системы; 9 - системы с сосредоточенными параметрами (сосредоточенные системы);

10 - системы с распределенными параметрами (распределенные системы)

МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ.

7. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ СИСТЕМЫ

7.а ПРЕОБРАЗОВАНИЕ ЛАПЛАСА

Далее будем широко пользоваться понятием преобразования Лапласа (интеграла Лапласа); при ведем основные сведения, относящиеся к понятию интеграла Лапласа.

Введем понятие интеграла Лапласа, пользуясь определением интеграла Фурье. Прямое одностороннее преобразование Фурье определяется формулой

Как известно, преобразование Фурье может быть применено к функциям x(t), для которых интеграл

существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при исследовании систем: l(t), Asin( t), еαt, Acos( t), некоторые решения дифференциальных уравнений.

Для того чтобы иметь возможность подобную функцию x(t) преобразовать по Фурье, предварительно ее надо умножить на функцию е-σtгде вещественное число σ>σ0выбрано таким образом, чтобы интеграл

18

был сходящимся.

В результате приведенныхрассуждений запишем

Введем новую комплексную переменную p = σ + jωполучим

Функция Х(p), определяемая зависимостью (1.4), где х (t) - оригинал, s = σ + jω, называется изображением х(t) и обозначается

p p

Часто интеграл (1.4) называют интегралом Лапласа. Ему присущи следующие свойства:

1.Линейность:

2.Смещение в комплексной области:

3.Смещение в действительной области:

4.Изображение производной:

p p

5.Изображение от интеграла:

p

p

6.Дифференцирование изображения:

8.Свертка функций в действительной области:

p p

9.Свертка в комплексной области:

p

7.б ПЕРЕДАТОЧНАЯ ФУНКЦИЯ И ЕЕ СВОЙСТВА

Рассмотрим замкнутую автоматическую систему. Предварительно дадим определение: схема системы, в которой указаны математические модели ее элементов (например, в форме дифференциальных уравнений), называется структурной схемой.

Представим структурную схему в виде, изображенном на рис. 1.38.

19

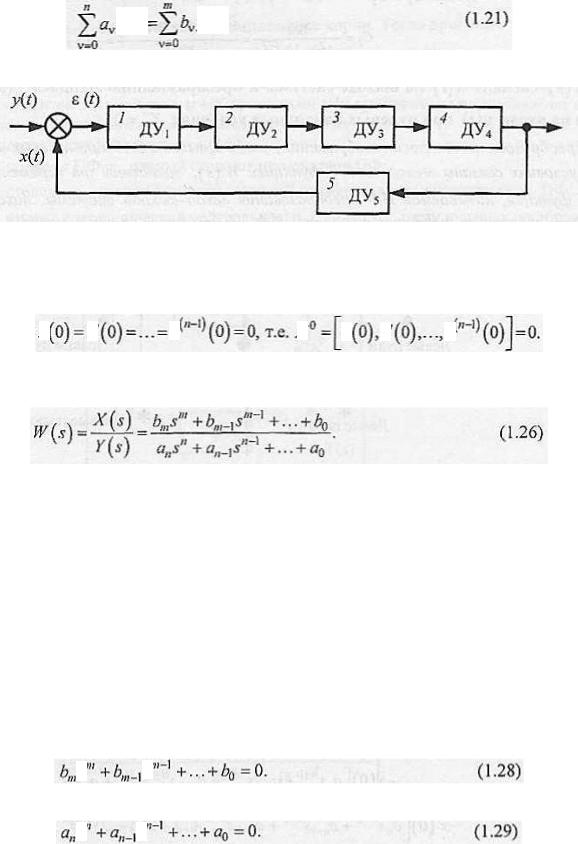
Поскольку полагаются известными дифференциальные уравнения ДУ1ДУ2,ДУ3, ДУ4, ДУ5 всех элементов, то, пользуясь каким-либо из методов, можно построить одно уравнение, связывающее вход системы с ее выходом.

Положим, что уравнение имеет вид y(ν) x(ν).

САУ является одномерной линейной стационарной, поскольку ее поведение описывается скалярным линейным дифференциальным уравнением с постоянными коэффициентами.

Рис. 1.38. Структурная схема системы:

1 - регулятор; 2 - усилительное устройство; 3 - исполнительное устройство; 4 - объект управления: 5 - измерительная система

Дадим одно из ключевых в теории автоматического управления определений: передаточной функцией (ПФ) САУ называется отношение преобразования Лапласа Y(p) сигнала y(t) на выходе системы к преобразованию Лапласа X(p) сигнала на входе x(t) при нулевых начальных условиях Y 0= 0

Преобразования Лапласа (изображения) входа ивыхода САУ при нулевых начальных условиях связаны между собой функцией W(p), зависящей от переменной p. Эта функция, называемая ПФ преобразования «вход-выход» системы, находится заменой оператора дифференцирования d/dtна комплексную переменную p, и, таким образом, формально ПФ получается из ДУпосле замены в нем символа кратного дифференцирования на соответствующую степень p и деления образованного таким образом

т.е, изображение выходного сигнала равно изображению входа (воздействия), умноженному на ПФ системы.

Приведем некоторые свойства и показатели передаточных функций.

ПФ представляет собой дробно-рациональную функцию (см. (1.26)), причем в реальной системе порядок числителя т не превышает порядка знаменателя п, т.е., m≤n . Коэффициенты ПФ аν, ν = 0, n; bk, k = 0, m вещественны, поскольку они представляют собой функции от вещественных параметров системы.

Значения p, при которых ПФ обращается в нуль, называются нулями ПФ. Нули являются корнями уравнения

p p

Значения p, прикоторых ПФ обращается в бесконечность, называются полюсами ПФ. Полюсы являются корнями уравнения

p p

Передаточная функция W(p) имеет, таким образом, т нулей и п полюсов. Как нули, так и полюса могут быть действительными или комплексно-сопряженными, поэтому их можно изобразить на комплексной плоскости (p-плоскости) (рис. 1.39).

20