лекции / В. А. Бородавкин, И. Л. Петрова -ТАУ дискретных систем / 6.1 Лекция

4

6 Лекция

Математические модели импульсных систем в виде разностных уравнений и структурных схем.

6.2 Построение дискретной модели стационарной стохастической системы

Здесь мы коротко остановимся на алгоритме дискретизации системы линейных дифференциальных уравнений. Алгоритм позволяет моделировать процессы в СУ с помощью рекуррентных процедур.

Пусть линейная стохастическая система описывается матричным дифференциальным уравнением

(7)

где - матрицы постоянных коэффициентов порядков ; Х – n –мерный вектор-столбец; - n-мерный гауссовский «белый шум», т.е. векторный процесс, компоненты которого - независимые между собой гауссовские процессы с нулевым математическим ожиданием и корреляционной функцией

.

Здесь - -функция Дирака, «Т» - символ транспонирования.

Перейдем от дифференциального уравнения (7) к дискретной модели. Запишем уравнение (7) в следующем виде:

(8)

где - матричный экспоненциал, т.е. матричная функция времени t, определяемая матричным рядом

I – единичная матрица. Элементами матричного экспоненциала являются весовые функции системы (7). Для матричного экспоненциала известно следующее свойство:

Введем шаг дискретизации , тогда в момент вектор Х() определится из соотношения

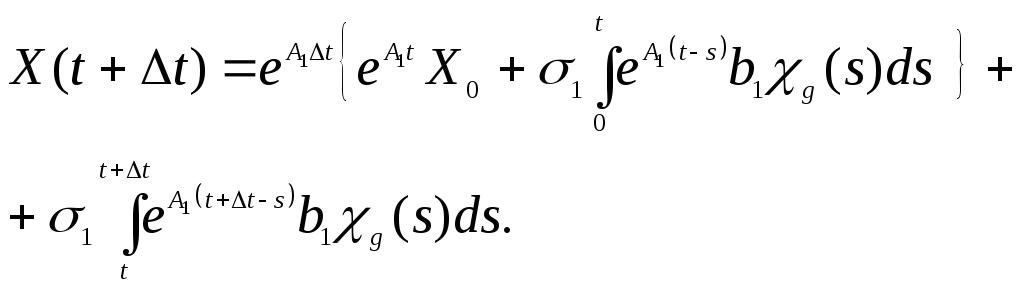(9)

Из (8) и (9) следует, что полученная после дискретизации последовательность удовлетворяет уравнению

(10)

Здесь

(11)

а гауссовские вектора и - независимы.

Компоненты матрицы А равны значению весовых функций в момент . Из условия равенства нулю математического ожидания

следует, что . Корреляционная матрица n – мерного вектора равна:

Так как корреляционная матрица процесса равна то двойной интеграл обращается в однократный:

После замены переменной интегрирования интеграл примет вид

(12)

Поэтому корреляционная матрица К векторов не зависит от момента времени t. Отметим, что матрица имеет порядок . Элементами являются весовые функции системы (7) по входу .

Из (10) следует, что при корреляционная матрица вектора определяется рекуррентным соотношением

(13)

При существует предел (13)

представляющий корреляционную матрицу стационарного СП на выходе системы (7).

Представим К в виде

(14)

где В – матрица порядка , r – ранг матрицы К. Используя (14), получаем уравнение дискретной модели СУ:

(15)

Здесь r – мерные вектора - удовлетворяют условиям и при . Стационарное решение уравнений (7) и (15) может быть получено, если корреляционная матрица начального условия равна .

Изложенные выше соотношения позволяют строить удобный для реализации на ЭВМ и экономичный вычислительный алгоритм моделирования линейных стохастических систем.

Алгоритм моделирования.

Исходными данными алгоритма являются матрицы , параметр и шаг дискретизации . Алгоритма предполагает проведение вычислений в следующей последовательности.

1. Вычисление матрицы А.

Из (11) следует, что i-тый столбец матрицы А равен:

где - n-мерный вектор, все компоненты которого, за исключением i-той, равны нулю. Из (8) следует, что является решением системы

(16)

в момент времени . Поэтому для вычисления матрицы А необходимо n раз интегрировать однородную систему (16) на промежутке при начальных условиях

2. Вычисление матрицы К

Элементы симметричной матрицы К определяются соотношениями

(17)

где элемент матрицы является i-той компонентой вектора , удовлетворяющего системе

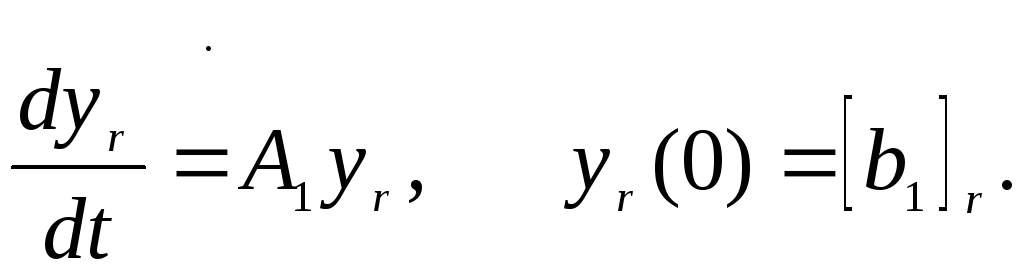(18)

Здесь - r – й столбец матрицы . Поэтому вычисление элементов осуществляется путем одновременного интегрирования системы (18) и уравнений

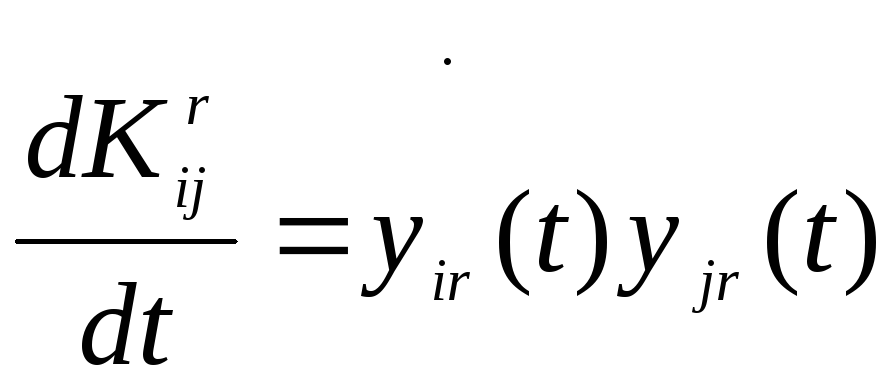(19)

на промежутке при нулевых начальных условиях для функций . После m-кратного интегрирования системы (18), (19) элементы матрицы К получаются суммированием .

При операция суммирования элементов может быть учтена с помощью начальных условий вводимых при вычислении по следующему алгоритму:

(20)

3. Вычисление матрицы .

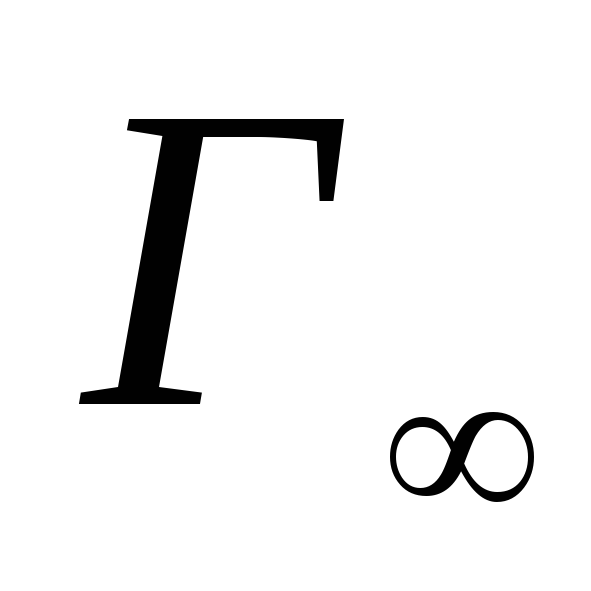Определение осуществляется с помощью рекуррентной процедуры (13) при нулевых начальных условиях.

4) Вычисление матрицы .

Матрица В определяется условием и находится с помощью известных процедур.

5) Начальное условие формируется как гауссовский случайный вектор . Эти операции заканчивают подготовительный этап вычислений. Цифровое моделирование осуществляется (после определения А, В, ) по формуле (15).